Результаты конкурса "Кенгуру-2019"
 |
Подведены итоги конкурса "Кенгуру-2019". Международная математическая игра-конкурс "Кенгуру-2019" проводилась 21 марта 2019 года. 140 098 учащихся из 2 652 учреждения образования Республики Беларусь приняли участие в самом массовом математическом соревновании школьников в мире. |
21 марта 2019 года учащиеся из 80 стран пяти континентов приняли участие в Международном математическом конкурсе "Кенгуру-2019". Задания конкурса были подготовлены лучшими математиками, учителями и преподавателями из стран-участниц и утверждены на конференции Ассоциации «Кенгуру» без границ» в 2018 году в Вильнюсе.
В нашей стране в этот день задачи решали 140 098 учащихся. По сравнению с прошлым учебным годом количество участников уменьшилось на 4318 (3%). Снижение численности участников произошло в шести регионах из семи. Исключение составил г. Минск, в котором число участников игры-конкурса увеличилось на 0,4%. Наибольший процент уменьшения количества участников отмечен в Гомельской области – 8,5%. На 6,1% уменьшилось количество участников в Гродненской области. Далее следуют Брестская область –– 4%, Могилёвская область –– 3,3%, Минская и Витебская области, в которых число участников уменьшилось на 1,9% и 1,4% соответственно. Следующая диаграмма отображает распределение участников по регионам:
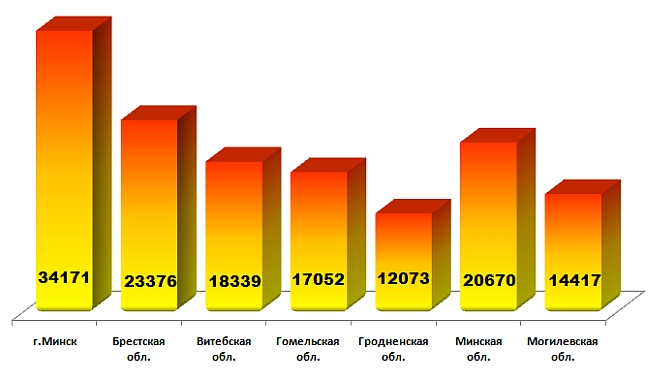
Задания «Кенгуру» разрабатываются для шести возрастных групп: для 1-2, 3-4, 5-6, 7-8, 9-10 и 11 классов. Распределение участников в соответствии с классами следующее:
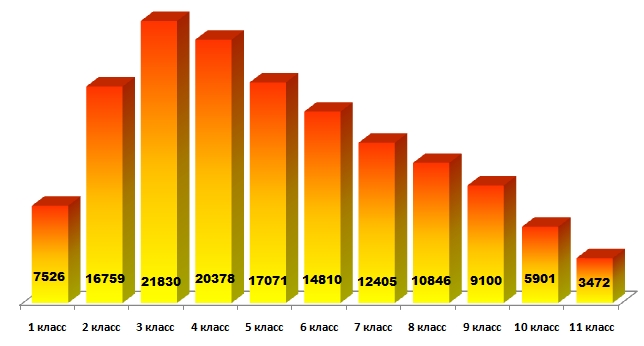
Напомним, что по правилам конкурса все задачи в задании условно разбиты на три уровня сложности: простые и занимательные вопросы, каждый из которых оценивается в 3 балла; более сложные задачи, для решения которых иногда требуется хорошее знание школьной программы по математике, оцениваются в 4 балла; и, наконец, сложные, нестандартные задачи, для решения которых надо проявить смекалку, умение рассуждать, оцениваются в 5 баллов. Успешность выполнения заданий отражена на следующих диаграммах.
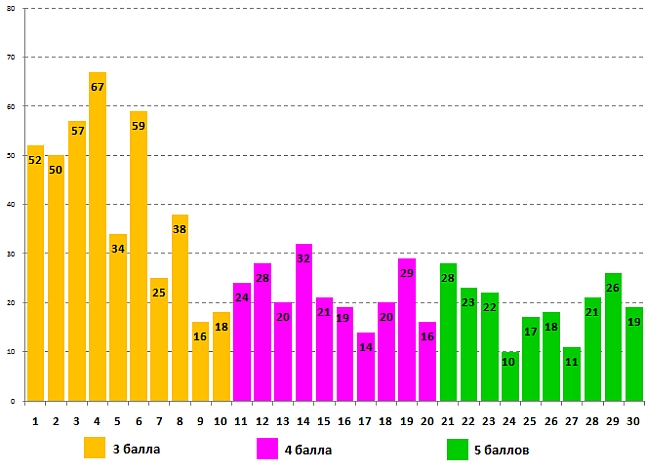
Информация об успешности выполнения задания для 1-2 классов, над которым трудились самые юные участники:
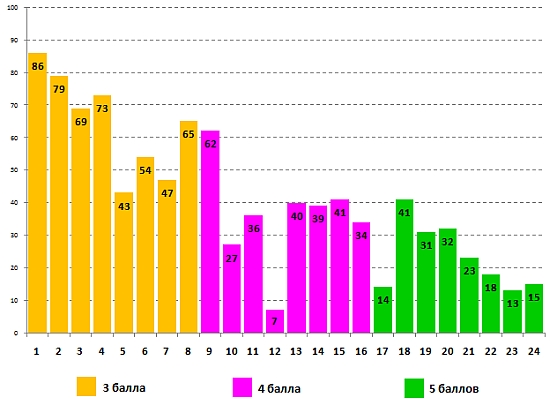
Успешность выполнения задания для 1-2 классов учащимися 2 класса:
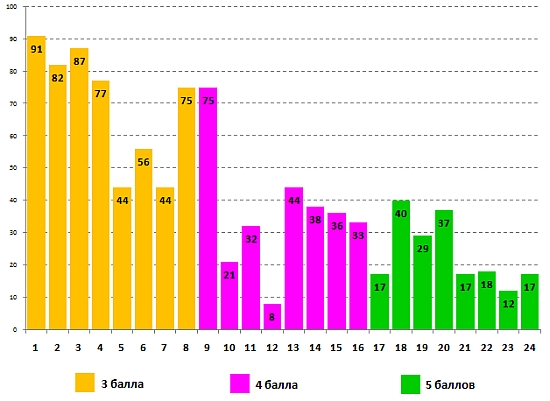
Возникает вопрос: почему, решая одни и те же задачи, первоклассники с некоторыми из них, а точнее почти с половиной, справляются лучше, чем второклассники? Так, самые юные математики в процентном отношении более успешно решили задачи №№7, 10, 11, 14, 15, 16, 18, 19, 21 и 23, а задача №22 была решена одинаково успешно первоклассниками и второклассниками.
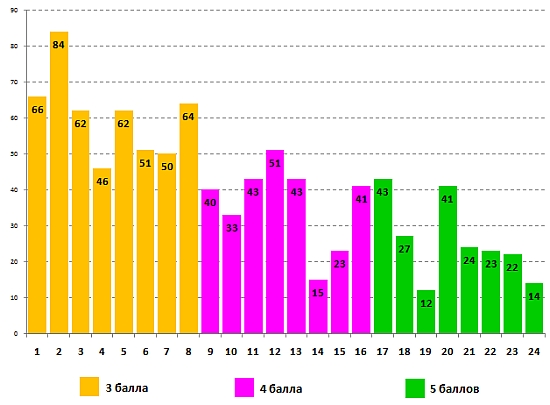
Успешность выполнения задания для 3-4 классов третьеклассниками:
Успешность выполнения задания для 3-4 классов учащимися 4 класса:
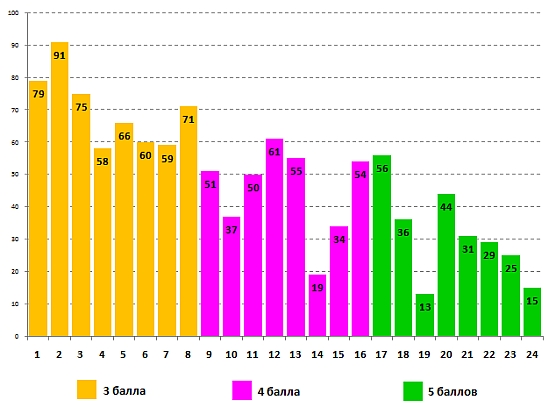
В этом задании четвероклассники подтвердили более высокий уровень знаний по сравнению с третьеклассниками, показав более высокий результат при решении всех задач, что является вполне логичным и закономерным.
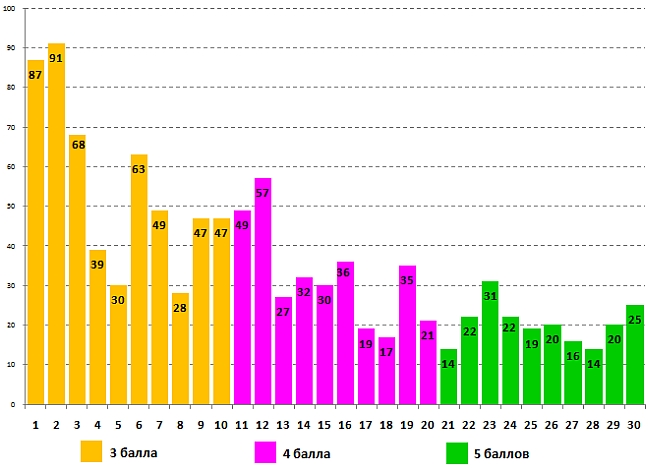
Статистические данные о выполнении задания для 5-6 классов учащимися 5 класса:
Успешность выполнения задания для 5-6 классов учащимися 6 класса:
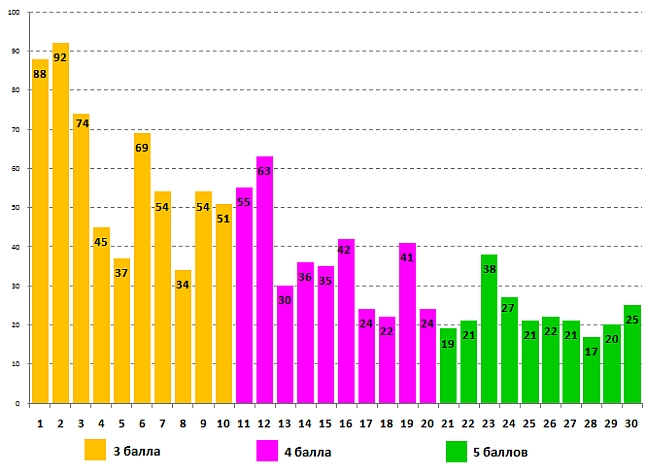
В этом задании шестиклассники, как и четвероклассники, подтвердили, что за год учебы приобрели знаний по математике больше, чем их имели пятиклассники. Только задача №22 была решена учащимися 5 класса более успешно в процентном отношении, а задачи №29 и №30 были решены с одинаковым успехом. У всех остальных задач задания процент правильных ответов у шестиклассников выше, чем у пятиклассников.
Данные об успешности выполнения задания для 7-8 классов учащимися 7 класса:
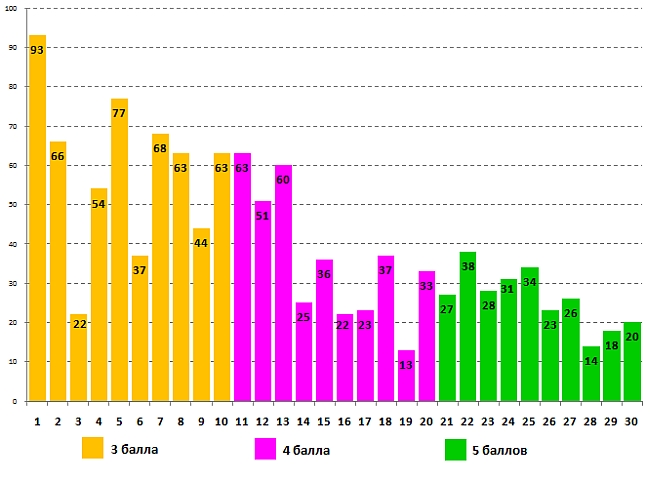
Данные о выполнении задания для 7-8 классов участниками – учащимися 8 класса:
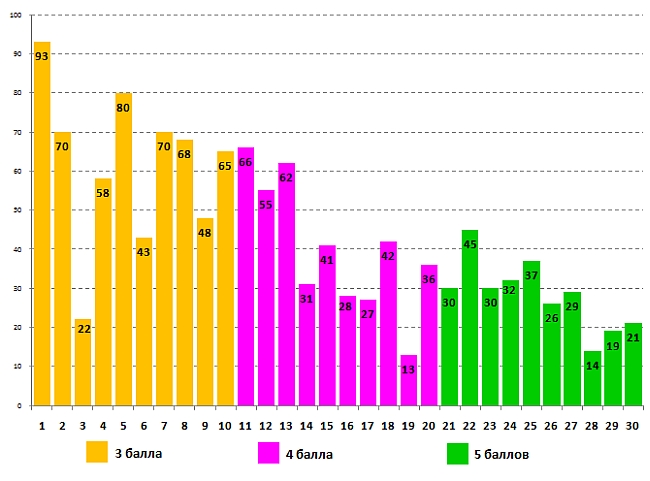
Сравнительный анализ успешности выполнения задания свидетельствует, что процент правильно решённых задач выше у старших ребят, только задачи №№1, 3, 19 и 28 решены одинаково успешно ребятами из разных параллелей.
Информация об успешности выполнения задания для 9-10 классов, над которым трудились девятиклассники:
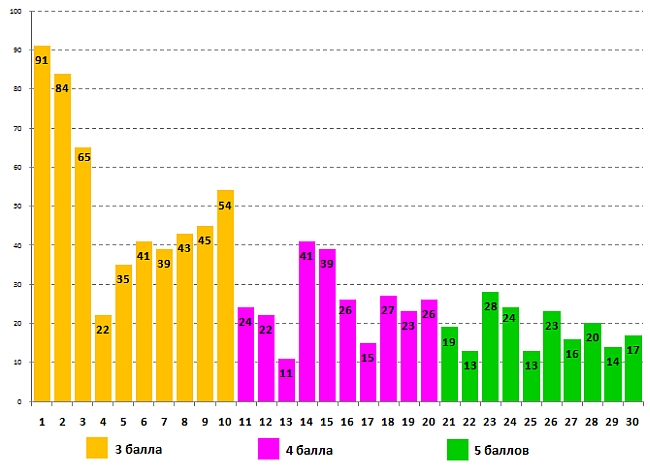
Успешность выполнения задания для 9-10 классов учащимися 10 класса:
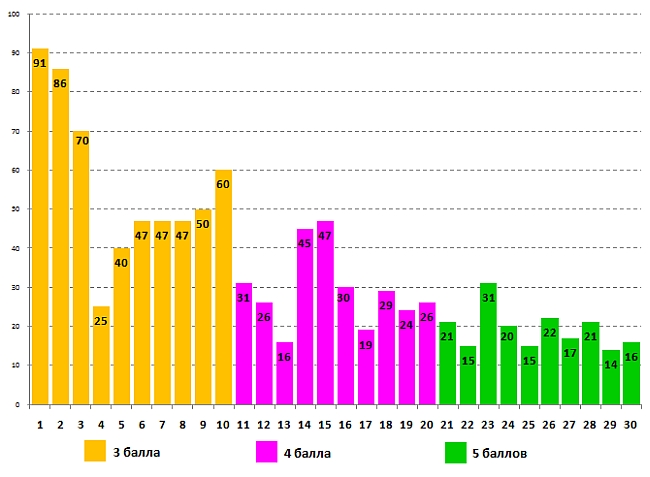
Одинаково успешно девятиклассники и десятиклассники справились с решением задач №№1, 20 и 29. Более высокий процент правильных ответов девятиклассники показали, решая задачи №№24, 26 и 30.
Информация об успешности выполнения задания учащимися 11 класса:
Следующая диаграмма характеризует уровень сложности заданий в целом. Она знакомит со средними баллами по стране для каждой параллели:
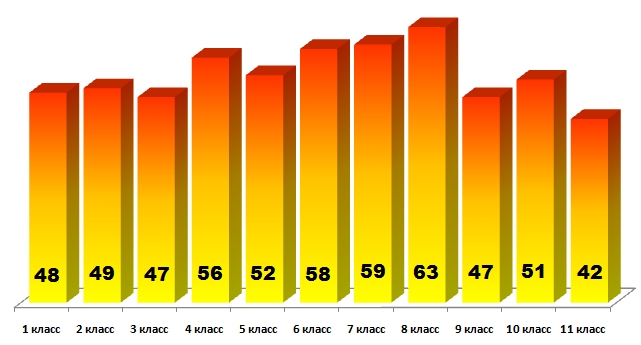
Как видно из диаграммы, самое трудное задание оказалось у одиннадцатиклассников.
Организаторы напоминают участникам, что в течение месяца результаты являются предварительными. На протяжении этого периода принимаются и рассматриваются обращения и замечания участников и организаторов в учреждениях и отделах образования. Через 1 месяц после размещения на сайте предварительные результаты конкурса объявляются окончательными и никаким изменениям более не подлежат.
Зарегистрированные на сайте участники после размещения окончательных результатов смогут добавить в свой личный кабинет результат своего участия в игре-конкурсе и получить электронный вариант свидетельства участника.
Организаторы выражают благодарность учителям, координаторам в учреждениях, отделах и управлениях образования за возможность учащимся принять участие в самом массовом математическом соревновании школьников в мире.
Значение математической науки невозможно переоценить. Ещё в XVI—XVIII веках благодаря успешному развитию математики все естественные науки были перестроены на базе создания новых математических моделей, и это привело к колоссальному их прогрессу. В связи с появлением компьютеров значительно выросла роль многих разделов математики, возникли новые науки — кибернетика, информатика, распознавание образов, теоретическое программирование, компьютерное моделирование и др.
Оргкомитет поздравляет всех участников игры-конкурса "Кенгуру-2019". Каждый участник получит приз «для всех». 20% учащихся, показавших лучшие результаты в своих учреждениях образования, будут поощрены дополнительными призами.
Всем участникам конкурса желаем дальнейших успехов в приобретении знаний, успешного завершения учебного года и реализации намеченных на лето планов!



