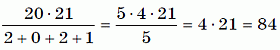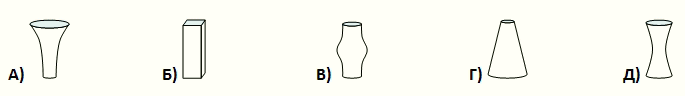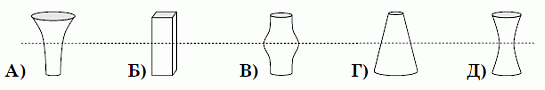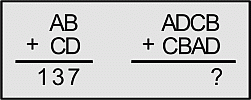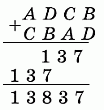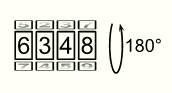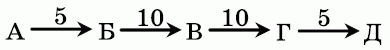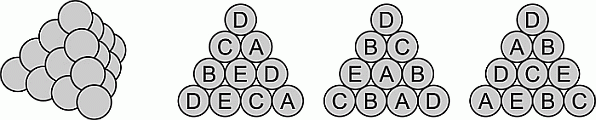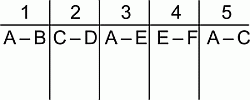Задание 1
|
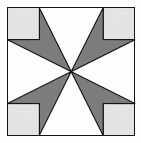
Какой из следующих знаков зодиака имеет ось симметрии?
A)  стрелец
стрелец
Б)  скорпион
скорпион
В)  лев
лев
Г)  рак
рак
Д)  козерог
козерог
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 30 - 0.75 = 29.25
|

Ось симметрии знака зодиака Стрелец показана на рисунке. Знаки зодиака в других вариантах ответа осей симметрии не имеют. Можно лишь отметить, что Рак  имеет центр (но не ось) симметрии.
имеет центр (но не ось) симметрии.
Задание 2
|
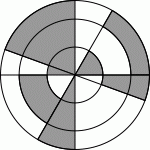
На рисунке показаны три концентрических круга с четырьмя отрезками, проходящими через их общий центр. Сколько процентов площади большего круга закрашены?
A) 30% Б) 35% В) 40% Г) 45% Д) 50%
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 29.25 + 3 = 32.25
|
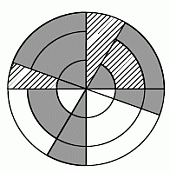
Отобразим симметрично относительно общего центра данных кругов серые фрагменты, расположенные ниже горизонтального диаметра. Другими словами, перекрасим их в белый цвет, а симметричные им (изначально белые, на рисунке заштрихованные) фрагменты перекрасим в серый цвет. В результате вся верхняя половина круга станет серой, а нижняя – белой. Следовательно, закрашена половина, т.е. 50% площади большего круга.
Задание 3
|
Чему равно значение выражения 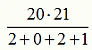 ?
?
A) 42 Б) 64 В) 80 Г) 84 Д) 105
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Задание 4
|
Сколько существует четырёхзначных чисел, цифры которых – последовательные натуральные числа, записанные в порядке возрастания слева направо?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Существует 6 таких чисел: 1234, 2345, 3456, 4567, 5678 и 6789.
Задание 5
|

Если правильно сложить 5 плиток пазла, получится прямоугольник с примером на вычитание. Чему равен результат вычислений в этом примере?
A) –100 Б) -8 В) -1 Г) 199 Д) 208
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Понятно, что одна из двух плиток с цифрой 2 должна быть крайней левой, а другая – крайней правой. Далее, с крайней левой плиткой может быть соединена справа только плитка со знаком «–», а с крайней правой может быть соединена слева только плитка с цифрой 0. Тогда среднее место займёт плитка с цифрой 1. В результате получаем выражение 2 – 102.
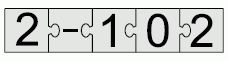
Его значение равно –100.
Задание 6
|
Каждая из пяти следующих ваз имеет одинаковую высоту и объем в 1 литр. В каждую вазу налили по поллитра воды. В какой вазе уровень воды самый высокий?
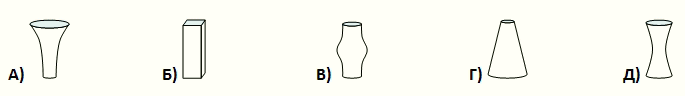
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Мысленно проведём горизонтальные плоскости на уровне, равном половине высоты данных фигур (ваз). Фигуры Б), В) и Д) симметричны относительно этой плоскости. Поэтому уровень воды в этих вазах совпадает с уровнем данной плоскости. У фигуры А) нижняя часть
(т.е. часть, расположенная ниже данной плоскости) уже, чем верхняя. Поэтому объём нижней части меньше объёма верхней части, и, значит, уровень жидкости в данной вазе выше уровня данной плоскости. А у фигуры Г) – всё наоборот. Следовательно, самый высокий уровень воды – в вазе А).
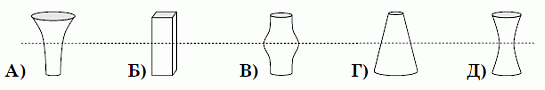
Задание 7
|
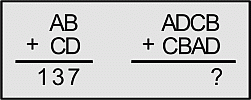
Школьник правильно сложил два двузначных числа в левой части доски и получил 137. Какой результат получится, если правильно сложить четырёхзначные числа в правой части доски?
A) 13737 Б) 13837 В) 14747 Г) 23737 Д) 137137
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 40.5 - 0.75 = 39.75
|
В условии дано: AB + CD = 137, и нужно найти ADCB + CBAD. Заметим, что у данных 4-значных чисел цифры в разрядах единиц такие же, как у чисел AB и CD. То же самое верно и для цифр десятков. Далее, цифры сотен совпадают с цифрами единиц, а цифры тысяч – с цифрами десятков. Поэтому
ADCB + CBAD = 13700 + 137 = 13837 (см. также рис.).
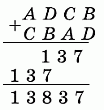
Задание 8
|
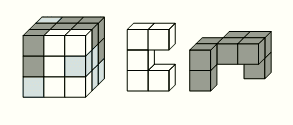
Куб 3 × 3 × 3 состоит из единичных кубиков чёрного, белого и серого цвета (см. рис.) Справа показаны фигуры, которые образуют все белые кубики и все чёрные кубики. Какую фигуру образуют все серые кубики?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 39.75 + 3 = 42.75
|
Сначала уберём фигуру, состоящую из белых кубиков, затем – из чёрных (см. рис.). Сравнивая полученный результат с вариантами ответа, видим, что правильным является ответ Д.

Задание 9
|
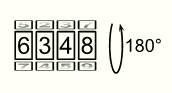
Велосипедный замок состоит из четырёх колец, на которых записаны в порядке возрастания цифры от 0 до 9. Чтобы получить правильный код, нужно каждое кольцо повернуть на 180° (см. рис.) Какой код замка правильный?
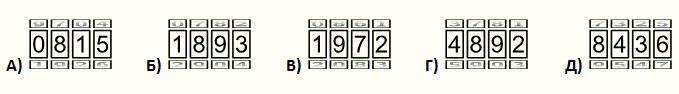
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 42.75 - 0.75 = 42
|
На каждом кольце находится 10 цифр. Если повернуть все кольца замка на 180° в направлении увеличения цифр, то цифры на них увеличатся на 5. Но после цифры 9 следует цифра 0. Поэтому в том в случае, когда при добавлении 5 будет получаться двузначное число, нужно заменить его последней цифрой полученной суммы. Проделав такие преобразования с числом 6348, получим число 1893.
По-другому ответ можно получить так. Выпишем числа от 0 до 9 по кругу так, как они расположены на кольце.
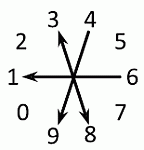
После поворота кольца на 180° все цифры поменяются местами с диаметрально противоположными. На рисунке стрелками показано, во что перейдут цифры числа 6348. Видим, что в результате получится число 1893.
Задание 10
|
Боря на 5 см выше Ани, но на 10 см ниже Васи. Гена на 10 см выше Васи, но на 5 см ниже Димы. Какое из следующих утверждений верно?
A) Аня и Дима одного роста.
Б) Аня на 10 см выше Димы.
В) Аня на 10 см ниже Димы.
Г) Аня на 30 см выше Димы.
Д) Аня на 30 см ниже Димы.
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 42 + 3 = 45
|
Условие задачи можно представить в виде схемы:
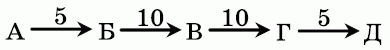
Здесь А, Б, В, Г и Д – заглавные буквы имён Аня, Боря, Вася, Гена и Дима. Стрелки направлены в сторону того, кто выше. Число над стрелкой указывает разницу в росте (в см). Видим, что разница в росте Ани и Димы составляет
5 +10 +10 + 5 = 30 см. Таким образом, правильным является ответ Д Аня на 30 см ниже Димы.
Задание 11
|
Прямоугольная плитка шоколада состоит из квадратных долек. Коля отломал две полные полоски и съел полученные 12 долек. Затем Дима отломал от оставшейся части одну целую полоску и съел 9 полученных долек. Сколько долек шоколада осталось в плитке?
A) 72 Б) 63 В) 54 Г) 45 Д) 36
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 45 - 1 = 44
|
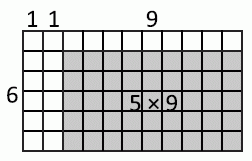
Так как две полные полоски, которые отломал от шоколадки Коля, состояли из 12 долек, то на одной полоске было 6 долек. Значит, одна из сторон шоколадки равна 6 (примем сторону одной дольки за 1). Далее, Дима отломал от полученного куска полоску, состоящую из 9 долек. Значит, ему от Коли достался кусок 6 × 9, а после того, как он съел отломанную полоску, остался кусок 5 × 9. То есть остался кусок, состоящий из 5 · 9 = 45 долек.
Задание 12
|
Банка, наполненная водой на одну пятую, весит 560 г. Та же банка, наполненная водой на четыре пятых, весит 740 г. Сколько весит пустая банка?
A) 60 г Б) 112 г В) 180 г Г) 300 г Д) 500 г
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 44 - 1 = 43
|
Заметим, что во втором случае воды в банке на 4/5 – 1/5 = 3/5 больше. При этом общий вес банки с водой больше на 740 – 560 = 180 г. Поэтому вода, заполняющая 3/5 банки, весит 180 г. Значит, вода, заполняющая 1/5 банки (именно столько её в первом случае), весит 180 : 3 = 60 г. Поэтому вес банки без воды равен 560 – 60 = 500 г.
По-другому задачу можно решить, составив уравнения. Пусть пустая банка весит Б г, а вода, заполняющая пятую часть банки – В г. Тогда, согласно условию,
Б + В = 560 и Б + 4В = 740.
Вычитая из второго уравнения первое, получаем 3В = 180, откуда В = 60. Тогда из первого уравнения
Б = 560 – 60 = 500.
Задание 13
|
Площадь большого квадрата на рисунке равна 16 см2, а площадь каждого маленького серого квадрата – 1 см2. Чему равна площадь тёмного цветка?
A) 3 см2
Б) 3,5 см2
В) 4 см2
Г) 5,5 см2
Д) 6 см2
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 43 + 4 = 47
|
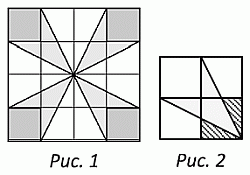
Согласно условию, данный квадрат есть квадрат 4 × 4. Разобьём его на единичные клетки (рис. 1). Цветок состоит из 4 одинаковых лепестков. Один лепесток вписан в квадрат 2 × 2 так, как показано на рис. 2. Сторонами клеток он разбит на 3 части: четырёхугольник и два равных треугольника (с катетами 1 и 0,5). Эти треугольники, очевидно, равны заштрихованным треугольникам. Поэтому площадь одного лепестка равна площади одной клетки, т.е. равна 1 см2. Поэтому площадь всего цветка равна 4 см2.
По-другому площадь цветка можно найти так. Данный квадрат площади 16 см2 состоит из четырёх угловых квадратов площади 1 см2, четырёх равных белых треугольников и цветка (см. рис. 1). Сторона одного белого треугольника, лежащего на стороне данного квадрата, равна 2 см. Высота треугольника, проведённая к этой стороне, также равна 2 см. Поэтому площадь треугольника равна
0,5 ⋅ 2 ⋅ 2 = 2 см2.
Тогда площадь цветка равна
16 − 4 ⋅ 1 − 4 ⋅ 2 = 4 см2.
Задание 14
|
Костя построил новый забор в своём саду. Ему понадобилось 25 деревянных досок, каждая из которых имеет длину 30 дм. Он прибил эти доски с небольшими одинаковыми перекрытиями соседних досок, как показано на рисунке. Общая длина нового забора Кости составила 69 метров. Какова длина одного перекрытия?

A) 2,4 дм Б) 2,5 дм В) 3 дм Г) 4,8 дм Д) 5 дм
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 47 - 1 = 46
|
Если бы не было перекрытий, то забор имел бы длину 25 • 30 = 750 дм. Но, по условию, его длина
оказалась равна 690 дм. Следовательно, перекрытия составляют 750 – 690 = 60 дм. Число перекрытий при соединении 25 досок равно 24. Поэтому длина одного перекрытия равна 60 : 24 = 2,5 дм.
Задание 15
|
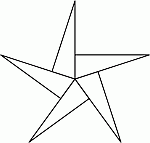
Пять одинаковых прямоугольных треугольников расположены так, что они, соприкасаясь бóльшими острыми углами, образуют звезду. Сколько всего потребуется таких треугольников, чтобы аналогично построить звезду, у которой соприкасаются меньшие острые углы?
A) 10 Б) 12 В) 18 Г) 20 Д) 24
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 46 - 1 = 45
|
Бóльшие из пяти острых углов данных треугольников имеют общую вершину и образуют вместе угол в 360°. Поэтому бóльший угол треугольника равен 360° : 5 = 72°. Тогда меньший угол равен 90° – 72° = 18°. Поэтому, чтобы построить звезду, соединив аналогичным образом острые углы таких треугольников, понадобится 360° : 18° = 20 треугольников.
Задание 16
|
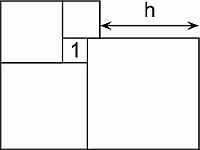
Пять квадратов расположены так, как показано на рисунке. Площадь меньшего из квадратов равна 1 см2. Чему равно h?
A) 3 см Б) 3,5 см В) 4 см Г) 4,2 см Д) 4,5 см
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 45 - 1 = 44
|
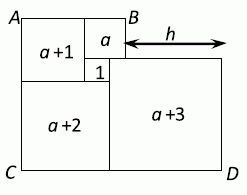
Пусть сторона верхнего квадрата (с вершиной B) равна a. Тогда сторона квадрата с вершиной A равна a + 1; сторона квадрата с вершиной С равна a + 2; сторона квадрата с вершиной D равна a + 3 (см. рис.). Поэтому
h = CD – AB = (a + 2) + (a + 3) – (a + 1) – a = 4.
Задание 17
|
Тест состоит из 20 вопросов. За каждый правильный ответ начисляется 7 баллов, за каждый неправильный ответ вычитается 4 балла. За каждый вопрос, оставленный без ответа, баллы не начисляются и не вычитаются. Эрик прошёл тест и набрал 100 баллов. Сколько вопросов он оставил без ответа?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 44 - 1 = 43
|
Пусть Эрик правильно ответил на a вопросов и неправильно на b вопросов (a и b – целые неотрицательные числа). Тогда, согласно условию,
a + b ≤ 20 и 7a – 4b = 100.
Из полученного равенства следует, что b ≠ 0, иначе 7a = 100, что невозможно, так как 100 не делится на 7. Далее,
поскольку 100 делится на 4, из данного равенства следует, что a делится на 4. Пусть a = 4n, где n – целое неотрицательное число. Тогда
7 · 4n – 4b = 100, или 7n – b = 25,
откуда следует, что n ≥ 4, иначе левая часть последнего равенства заведомо меньше 25 (противоречие). С другой стороны, n не может быть больше 4, иначе
a = 4n ≥ 4 · 5 = 20, и тогда a + b > 20, так как b > 0. Следовательно,
n = 4 и b = 7 · 4 – 25 = 3.
Тогда a + b = 4 · 4 + 3 = 19. Поэтому Эрик оставил без ответа 20 – 19 = 1 вопрос.
Задачу можно решить и без составления уравнений и неравенств. Если Эрик набрал 100 баллов, то он правильно ответил не менее чем на 15 вопросов. Действительно, за другие вопросы (без ответа и с неправильными ответами) он либо не получал баллов, либо получал штрафные баллы, которые только уменьшают сумму. Поэтому если бы правильных ответов было не более 14, то сумма набранных баллов была бы не больше 14 · 7 = 98. Далее, пусть Эрик правильно ответил ровно на 15 вопросов. Тогда за них он получил 15 · 7 = 105. Получаем лишние 105 – 100 = 5 баллов. Но 5 не делится на 4, и поэтому лишние баллы нельзя убрать за счёт неправильных ответов. Значит, правильных ответов больше 15. Пусть Эрик правильно ответил ровно на 16 вопросов. Тогда за них он получил 16 · 7 = 112 баллов. Если при этом он неправильно ответил на
(112 – 100) : 4 = 3 вопроса, то в результате у него получается ровно 100 баллов, как и требуется. При этом у него остаётся
20 – 16 – 3 = 1 вопрос без ответа. Если бы Эрик ответил правильно на 17 или более вопросов, то даже если бы он на все остальные вопросы ответил неправильно, он набрал бы не менее
17 · 7 – 3 · 4 = 107 баллов, что противоречит условию. Видим, что есть только одна возможность получить 100 баллов, при которой только 1 вопрос оставлен без ответа.
Задание 18
|
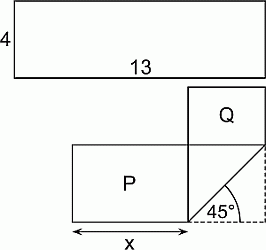
Прямоугольную полоску бумаги размером 4 × 13 согнули, как показано на рисунке. При этом образовались два прямоугольника с площадями P и Q, причём P = 2Q. Чему равен x?
A) 5 Б) 5.5 В) 6 Г) 6.5 Д) 4√2
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 43 - 1 = 42
|
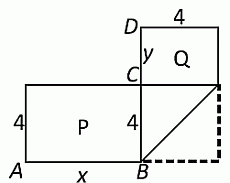
Отрезки AB и BD вместе составляют большую сторону данной полоски 4 × 13 (см. рис.). Поэтому AB + BD = 13. Далее, длина отрезка BC равна ширине данной полоски и, значит, BC = 4. Тогда
x + 4 + y = 13, откуда y = 9 – x.
Так как, по условию P = 2Q, имеем:
4x = 2 · 4(9 – x), или x = 18 – 2x, или 3x = 18, откуда x = 6.
Задание 19
|
В корзине с фруктами в два раза больше яблок, чем груш. Кристина и Лиля разделили между собой все фрукты так, что у Кристины оказалось в два раза больше фруктов, чем у Лили. Какое из следующих утверждений заведомо верно?
A) У Кристины есть хотя бы одна груша.
Б) У Кристины в два раза больше яблок, чем груш.
В) У Кристины вдвое больше яблок, чем у Лили.
Г) У Кристины столько яблок, сколько у Лили груш.
Д) У Кристины столько груш, сколько яблок у Лили.
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 42 - 1 = 41
|
По условию, яблок в два раза больше, чем груш, и Кристина получила фруктов в два раза больше, чем Лиля. Поэтому один из способов, как могли распределиться фрукты: все яблоки достались Кристине, а все груши – Лиле. Теперь, любое другое распределение фруктов между Кристиной и Лилей, не меняющее соотношение фруктов x = 6, можно получить, если Кристина отдаст Лиле несколько своих яблок и получит от неё столько же груш. Это показывает, что верно утверждение у Кристины столько груш, сколько яблок у Лили.
Задание 20
|
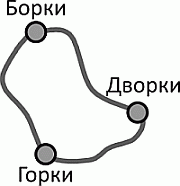
Три деревни соединены дорогами, как показано на рисунке. Путь от Горок до Борок через Дворки на 1 км длиннее дороги, соединяющей Горки и Борки. Путь от Дворок до Борок через Горки на 5 км длиннее дороги, соединяющей Дворки и Борки. Путь от Дворок до Горок через Борки на 7 км длиннее дороги, соединяющей Дворки и Горки. Какова длина самой короткой дороги, соединяющей две из этих трёх деревень?
A) 1 км Б) 2 км В) 3 км Г) 4 км Д) 5 км
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 41 - 1 = 40
|
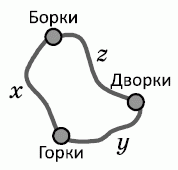
Пусть длины дорог между данными деревнями равны x, y и z км, как показано на рисунке. Тогда, согласно условию,
y + z = x + 1, (1)
y + x = z + 5, (2)
z + x = y + 7. (3)
Сложив (1) и (2), получим
2y + z + x = x +z + 6,
т.е. 2y = 6, откуда y = 3. Аналогично, сложив (1) и (3), получим z = 4. Наконец, сложив (2) и (3), получим x = 6. Видим, что длина самой короткой дороги равна 3 км.
Задание 21
|
У некоторой дроби числитель и знаменатель положительны. Числитель увеличили на 40%. На сколько процентов следует уменьшить её знаменатель, чтобы новая дробь стала в два раза больше исходной?
A) 10% Б) 20% В) 30% Г) 40% Д) 50%
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 40 - 1.25 = 38.75
|
Пусть a/b данная дробь. После увеличения числителя a на 40% он станет равен 1,4a. Пусть x – знаменатель новой дроби, удовлетворяющей условию задачи. Тогда
1,4a/x = 2⋅a/b, откуда 1,4b = 2x, или x = 0,7b. Это означает, что x составляет 70% от b. Следовательно, знаменатель b нужно уменьшить на 100% – 70% = 30%.
Задание 22
|
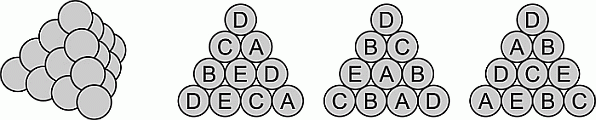
Треугольная пирамида построена из 20 шаров одинакового радиуса. Каждый шар помечен одной из букв A, B, C, D или E. Каждой буквой помечено ровно 4 шара. На рисунках показаны метки шаров на трёх боковых гранях этой пирамиды. Какая метка у центрального шара нижней грани?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 38.75 + 5 = 43.75
|
Верхний шар пирамиды можно видеть на всех трёх боковых гранях, другие шары на боковых рёбрах видны на двух боковых гранях, центральный шар и два средних нижних шара боковой грани видны только на одной грани. Единственный шар, который не виден ни на одной боковой грани, – это центральный шар нижней грани. Его метку и нужно определить. Учитывая сделанные наблюдения, можно определить, что на боковых гранях пирамиды находится только 3 шара D и по 4 шара с остальными метками. Соответствующие подсчёты приведены в таблице.
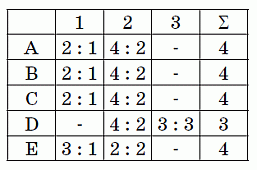
Следовательно, центральный
шар нижней грани имеет метку D.
Задание 23
|
Шестизначное число 2ABCDE умножили на 3, и в результате получилось шестизначное число ABCDE2. Какова сумма цифр данного числа?
A) 24 Б) 27 В) 30 Г) 33 Д) 36
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 43.75 + 5 = 48.75
|
Обозначим пятизначное число ABCDE через x. Тогда данное шестизначное число
2ABCDE = 200000 + x, а шестизначное число
ABCDE2 = 10x + 2. Согласно условию,
3 (200000 + x) = 10x + 2.
Решая это уравнение, получаем:
600000 + 3x = 10x + 2, или
599998 = 7x, откуда x = 85714. Тогда данное шестизначное число – это число 285714. Его сумма цифр равна
2 + 8 + 5 + 7 + 1 + 4 = 27.
По-другому цифры числа ABCDE можно определить так. Из равенства
3 · 2ABCDE = ABCDE2 видим, что 3 · E заканчивается на 2. Это возможно, только если E = 4. В результате имеем:
3 · 2ABCD4 = ABCD42. Рассмотрим две последние цифры. Произведение 3 · D4 должно заканчиваться на 42. Так как
3 · 4 = 12 и 42 – 12 = 30, то 3 · D должно заканчиваться на 3. Подходит только D = 1. Теперь имеем:
3 · 2ABC14 = 2ABC142. Произведение 3 · С14 должно заканчиваться на 142. Так как
3 · 14 = 42 и 142 – 42 = 100, то 3 · C должно заканчивать на 1. Подходит только C = 7. Поэтому имеем:
3 · 2AB714 = 2AB7142. Произведение 3 · B714 должно заканчиваться на 7142. Так как
3 · 714 = 2142 и
7142 – 2142 = 5000, то 3 · B должно заканчиваться на 5. Подходит только B = 5. Наконец, имеем:
3 · 2A5714 = 2A57142. Произведение 3 · A5714 должно заканчиваться на 57142. Так как
3 · 5714 = 17142 и 57142 – 17142 = 40000, то 3 · A должно заканчиваться на 4. Подходит только A = 5. Таким образом, число 2ABCDE = 285714, его сумма цифр равна 27.
Задание 24
|
В коробке находятся только зелёные, красные, синие и жёлтые фишки. Известно, что среди любых 27 произвольно выбранных фишек всегда найдётся хотя бы одна зелёная фишка; среди любых 25 фишек – хотя бы одна красная; среди любых 22 фишек – хотя бы одна синяя; наконец, среди любых 17 фишек – хотя бы одна жёлтая. Какое наибольшее количество фишек может быть в коробке?
A) 27 Б) 29 В) 51 Г) 87 Д) 91
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
Пусть в коробке находится З зелёных, К красных, С синих и Ж жёлтых фишек. Поскольку среди любых 27 фишек в коробке есть хотя бы одна зелёная, то число других фишек не больше 26. В противном случае, можно было бы выбрать 27 не зелёных фишек. Имеем неравенство:
К + С + Ж ≤ 26.
Аналогично получаем ещё три неравенства:
З + С + Ж ≤ 24,
З + К + Ж ≤ 21 и
З + К + С ≤ 16.
Сложив все эти четыре неравенства, получим:
3 · (З + К + С + Ж) ≤ 87, откуда
З + К + С + Ж ≤ 29.
Итак, в коробке не более 29 фишек.
Попробуем составить нужный набор ровно из 29 фишек. В этом случае все выше полученные неравенства должны быть равенствами. Тогда
З + К + С + Ж = 29, и если
К + С + Ж = 26, то
З = 29 – 26 = 3; если
З + С + Ж = 24, то
К = 29 – 24 = 5; если
З + К + Ж = 21, то
С = 29 – 21 = 8; если
З + К + С = 16, то
Ж = 29 – 16 = 13.
Видим, что набор из 29 фишек существует и, значит, правильным является ответ 29.
Задание 25
|

Поверхность футбольного мяча состоит из белых шестиугольников и чёрных пятиугольников, как показано на рисунке. Общее количество пятиугольников равно 12. Сколько всего шестиугольников?
A) 12 Б) 15 В) 18 Г) 20 Д) 24
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 47.5 - 1.25 = 46.25
|
По условию, имеется 12 пятиугольников. У каждого пятиугольника 5 соседних (по общей стороне) шестиугольников. Если бы у разных пятиугольников все соседние шестиугольники были различны, то число шестиугольников было бы равно 12 · 5 = 60. Но у каждого шестиугольника имеется 3 соседних пятиугольника. Поэтому 60 – это утроенное число шестиугольников, т.е. на самом
деле их количество равно 60 : 3 = 20.
По-другому найти ответ можно, подсчитывая количество вершин данных многоугольников. С одной стороны, пятиугольников 12 и каждая вершина принадлежит ровно одному пятиугольнику. Поэтому число всех вершин равно 12 · 5 = 60. С другой стороны, пусть число шестиугольников равно n. Так как каждая вершина принадлежит ровно двум шестиугольникам, то количество всех вершин равно 6n : 2 = 3n. Имеем: 3n = 60, откуда n = 20.
Ещё один способ – рассмотреть рёбра данных многоугольников. Стянем в вершины все рёбра, которые являются общими у шестиугольников, т.е. преобразуем такие рёбра в вершины. Тогда все шестиугольники станут треугольниками. При этом каждое (оставшееся) ребро будет принадлежать ровно одному пятиугольнику и ровно одному треугольнику. Поэтому если число треугольников (а значит, и шестиугольников) равно n, то, подсчитывая число всех рёбер двумя способами, получим 5 · 12 = 3n, откуда n = 20.
Отметим, что многогранник, имеющий такой же вид, как мяч, в данной задаче, называется усечённым икосаэдром. Он является одним из 13 полуправильных многогранников (архимедовых тел). Ещё один полуправильный многогранник рассматривается в задаче №25 для 11 класса.
Задание 26
|
2021 кенгуру расставлены в ряд и пронумерованы числами от 1 до 2021. Каждый кенгуру окрашен в красный, серый или синий цвет так, что среди любых трёх подряд стоящих кенгуру встречаются кенгуру всех трёх цветов. Боря угадывал цвета пяти кенгуру и его предположения были: кенгуру 2 – серый; кенгуру 20 – синий; кенгуру 202 – красный; кенгуру 1002 – синий; кенгуру 2021 – серый. Оказалось, что Боря ошибся только один раз. Какой номер кенгуру, цвет которого Боря не угадал?
A) 2 Б) 20 В) 202 Г) 1002 Д) 2021
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 46.25 + 5 = 51.25
|
Заметим, что цвета кенгуру повторяются с периодом 3. Действительно, пусть A, B, C, D – четыре подряд стоящие кенгуру. Тогда мы имеем две тройки (A, B, C) и (B, C, D). В каждой тройке все три кенгуру разного цвета: красного, серого и синего. При этом в первой тройке цвет A отличен от цвета B и цвета C. Во второй тройке цвет D также отличен от цвета B и цвета C. Следовательно, кенгуру A и D – одного цвета.
В силу указанной периодичности цвет у разных кенгуру совпадает тогда и только тогда, когда номера этих кенгуру имеют одинаковые остатки при делении на 3. Числа 2, 20, 202, 102 и 2021 имеют при делении на 3 остатки 2, 2, 1, 0 и 2 соответственно (см. таблицу).
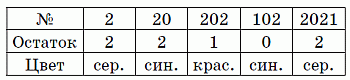
Поэтому цвета кенгуру с номерами 2, 20 и 2021 должны быть одинаковыми. Однако, по условию, они соответственно серый, синий и серый. Поэтому тот единственный кенгуру, цвет которого Боря не угадал, – это кенгуру из данной тройки (кенгуру номер 20).
Задание 27
|
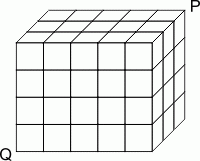
Деревянный параллелепипед размера 3 × 4 × 5 состоит из 60 единичных кубиков. Термит, прогрызая кубики, пробирается по диагонали от вершины Q до вершины P. Эта диагональ не пересекает рёбер ни одного из кубиков. Через сколько кубиков проходит путь термита?
A) 8 Б) 9 В) 10 Г) 11 Д) 12
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 51.25
По условию, путь термита не пересекает ни одного ребра. Поэтому, каждый раз переходя в следующий на пути следования кубик, термит перемещается в соседний по грани кубик: либо в правый, либо в передний, либо в верхний (см. рис. в условии задачи). При этом, чтобы перейти от вершины Q до вершины P, термит из исходного углового кубика должен переместиться на 4 кубика вправо, на 2 кубика вперёд и на 3 кубика вверх, всего – на
4 + 2 + 3 = 9 кубиков. С учётом исходного углового кубика, на пути находится 1 + 9 = 10 кубиков.
|
Задание 28
|
Население города составляет 2021 человек, из которых 2000 лжецов и 21 рыцарь. Лжецы всегда лгут, а рыцари всегда говорят правду. Волшебник разделил 2020 из горожан на 1010 пар. Каждый горожанин в паре назвал другого в своей паре рыцарем или лжецом. В результате, 2000 человек были названы рыцарями, а 20 – лжецами. Сколько было пар, состоящих из двух лжецов?
A) 980 Б) 985 В) 990 Г) 995 Д) 1000
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 51.25 - 1.25 = 50
|
Будем обозначать рыцарей буквой Р, а лжецов буквой Л. Созданные волшебником пары могли быть трёх типов: {Л, Л}, {Л, Р} и {Р, Р}. Так как лжецы всегда лгут, а рыцари всегда говорят правду, утверждения в парах могут быть только следующие:
{Л, Л} → {Р, Р}, {Л, Р} → {Л, Л}, {Р, Р} → {Р, Р}.
Видим, что лжецы названы только в паре типа {Л, Р}. А по условию, лжецами было названо 20 человек. Поэтому число пар {Л, Р} равно 10. Остальные пары – это пары типа {Л, Л} и {Р, Р}. Так как рыцарей в городе 21, и 10 из них вошли в пары {Л, Р}, то пары {Р, Р} могут быть образованы оставшимися 11 рыцарями. Ясно, что число таких пар равно 5, один рыцарь не вошёл ни в одну пару. Тогда, так как общее число пар всех типов равно 1010, число пар типа {Л, Л} равно
1010 – 10 – 5 = 995.
Задание 29
|
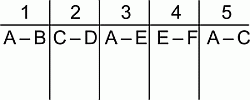
В турнире каждая из шести команд A, B, C, D, E и F сыграла с каждой из остальных один матч, т. е. в каждом из пяти кругов турнира одновременно проходили по три матча. Телеканал решил, что он будет показывать в каждом туре по одному матчу (см. таблицу трансляций матчей, где цифрами обозначены номера кругов). В каком круге турнира команда D играла против команды F?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Будем последовательно определять игры в раундах в дополнение к тем, которые указаны в условии задачи, и заполнять таблицу. Заметим, что изначально
указаны три игры с командой A, а именно A–B, A–E и A–C в 1, 3 и 5 кругах соответственно. Из двух оставшихся игр
команды A, а именно A–D и A–F, первая не может быть во 2-м туре, так как в этом туре D играет с С. Аналогично, игра A–F не может быть в 4 туре. Поэтому игры A–D и A–F проходили соответственно в 4 и 2 турах. Добавим эти результаты во вторую строчку таблицы.
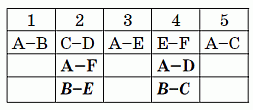
Теперь мы видим, что во 2 туре четыре команды A, D и F распределены по парам. Поэтому третью пару однозначно составляют две оставшиеся команды: B–E. Аналогично, в 4 туре третья пара – это B–C. Добавим эти игры в третью строчку таблицы.
В результате определены три игры команды C: C–D, B–C и A–C соответственно во 2, 4 и 5 турах. Тогда оставшиеся две игры C–E и C–F должны были состояться в 1 и 3 турах. При этом игра C–E не могла быть в 3 туре, так как в этом туре E играет с A. Поэтому игры C–E и C–F прошли соответственно в 1 и 3 турах. Вносим эти данные в таблицу. Далее, поскольку в 1 и 3 турах известны по две игры, то, как и раньше, однозначно определяются третьи игры: D–F и B–D в 1 и 3 турах соответственно.
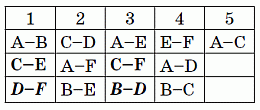
Таким образом, хотя мы ещё не заполнили таблицу целиком, ответ найден: игра D–F состоялась в первом туре. Но уже не составляет труда закончить заполнение таблицы.
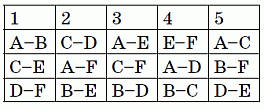
Задание 30
|
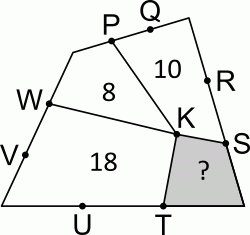
На рисунке изображён четырёхугольник, разбитый на четыре меньших четырёхугольника с общей вершиной K. Остальные отмеченные точки делят стороны большого четырёхугольника на три равные части. Числа, записанные внутри меньших четырёхугольников, указывают их площадь. Чему равна площадь серого четырёхугольника?
A) 4 Б) 5 В) 6 Г) 6,5 Д) 7
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 48.75 + 5 = 53.75
|
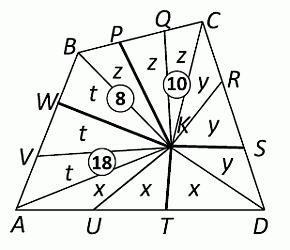
Соединим отрезками вершину K с вершинами данного четырёхугольника ABCD и отмеченными на его сторонах точками (см. рис.). В результате получаем разбиение данного четырёхугольника на треугольники с общей вершиной K. Заметим, что на каждой стороне данного четырёхугольника имеется по три равных стороны данных треугольников с общей высотой, проведённой к этим сторонам, или их продолжениям из вершины K. Поэтому площади таких троек треугольников одинаковые. С учётом этого отметим площади треугольников буквами x, y, z и t, как показано на рисунке. Согласно условию,
2y + 2z = 10, z + t = 8, 2x + 2t = 18
и требуется найти STKSD = x + y. После упрощений получим:
y + z = 5, z + t = 8, x + t = 9.
Сложим первое и третье из этих трёх уравнений, получим:
y + z + x + t = 14. Вычтем из полученного второе уравнение, получим: x + y = 6.
По-другому завершить вычисления можно было так. Заметим, что
SAWKT + SKPCS = 2(x + y + z + t) = 2 · (STKSD + SWBPK),
т.е. 18 + 10 = 2 · (STKSD + 8),
откуда 14 = STKSD + 8 , и STKSD = 6.



 стрелец
стрелец скорпион
скорпион лев
лев рак
рак козерог
козерог


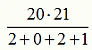 ?
?