Задание 1
|
У Эрики есть 4 кирпича: 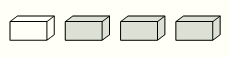 . Какой из следующих кубов она может из них сложить?
. Какой из следующих кубов она может из них сложить?

|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 24 - 0.75 = 23.25
|
По условию, у Эрики есть 1 белый и 3 серых кирпича. Только в варианте ответа В куб состоит из такого же набора кирпичей. Во всех других вариантах ответа имеется по 2 белых и 2 серых кирпича. Следовательно, правильным является ответ В.
Задание 2
|
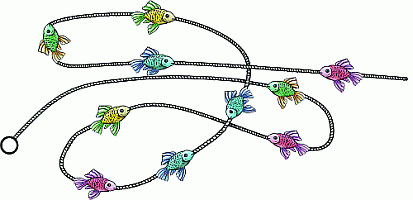
У скольких рыб головы будут направлены в сторону кольца, если распрямить леску на рисунке?
A) 3 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 23.25 + 3 = 26.25
|
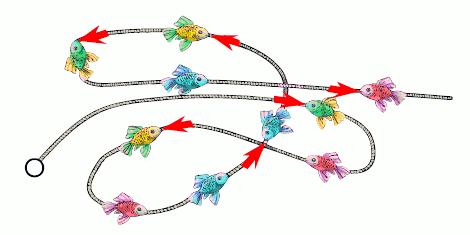
Будем продвигаться вдоль лески, начав с кольца, и отмечать стрелками рыбок, расположенных навстречу движению (см.
рис.). Видим, что число таких рыбок равно 6.
Задание 3
|

Если правильно сложить 4 плитки пазла, получится прямоугольник с примером на сложение. Чему равен результат вычислений в этом примере?
A) 6 Б) 15 В) 18 Г) 24 Д) 33
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 26.25 + 3 = 29.25
|
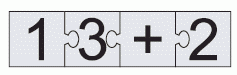
По форме плиток в условии задачи видно, что плитка с цифрой 1 может быть только самой левой, а плитка с цифрой 2 – только самой правой. Далее, плитка со знаком «+» может располагаться только между
плитками с цифрами 3 и 2 (см. рис.). Поэтому пример на сложение – это 13 + 2. Результат равен 15.
Задание 4
|

Оля нарисовала солнце. В каком из следующих ответов приведён фрагмент этого рисунка?

|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 29.25 - 0.75 = 28.5
|
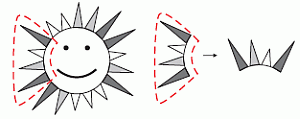
Показан фрагмент рисунка солнца, который после поворота совпадает с тем, который приведён в ответе Б. Можно непосредственно убедиться, что фрагментов в других вариантах ответа на рисунке солнца нет.
Задание 5
|
Пять мальчиков соревновались в стрельбе по мишени. Их мишени показаны в вариантах ответа. Алик набрал больше всего очков. Какая из следующих мишеней – его мишень?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 28.5 - 0.75 = 27.75
|
Подсчитаем суммы очков на мишенях. Получим:

Наибольшая сумма – на мишени Д). Значит, это и есть мишень, по которой стрелял Алик.
Задание 6
|
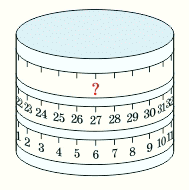
На цилиндр намотали мерную ленту, как показано на рисунке. Какое число стоит на месте, обозначенном знаком вопроса?
A) 33 Б) 42 В) 48 Г) 53 Д) 69
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 27.75 + 3 = 30.75
|
На рисунке в условии задачи видим, что над числом 6 после одного оборота стоит число 27. Значит, после каждого оборота числа, расположенные на одной вертикали, увеличиваются на 27 – 6 = 21. Поэтому на месте, обозначенном знаком вопроса, т. е. над числом 27, должно стоять число 27 + 21 = 48.
Задание 7
|
Денис запустил серебряную и золотую петарды. От взрыва золотой петарды образовалось на 6 звёзд больше, чем от взрыва серебряной, а всего при взрыве этих петард образовалось 20 звёзд. На сколько звёзд взорвалась золотая петарда?
A) 9 Б) 10 В) 12 Г) 13 Д) 15
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30.75 + 3 = 33.75
|
Если бы от взрыва серебряной петарды образовалось столько же звёзд, как от взрыва золотой, т. е. на 6 звёзд больше, то всего от двух петард их было бы 20 + 6 = 26. Поэтому от взрыва золотой петарды образовалось 26 : 2 = 13 звёзд.
Задание 8
|
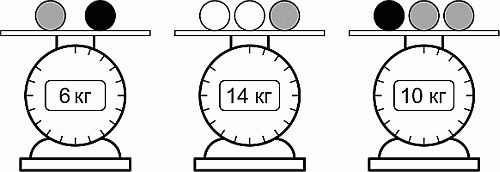
У Сюзанны есть несколько шариков трёх разных цветов. Шарики одинакового цвета имеют одинаковый вес. Она взвесила их, показания весов даны на рисунке. Сколько весит белый шарик?
A) 3 кг Б) 4 кг В) 5 кг Г) 6 кг Д) 7 кг
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 33.75 - 0.75 = 33
|
На третьих весах лежат такие же шары, как на первых весах, и ещё один серый шар (см. рис. в условии задачи). Поэтому, согласно показаниям на этих весах, серый шар весит 10 – 6 = 4 кг. Тогда, согласно показаниям на вторых весах, два белых шара весят 14 – 4 = 10 кг. Следовательно, один белый шар весит 10 : 2 = 5 кг.
Задание 9
|
У Миши есть три типа карточек: яблоко, вишня и виноград. Он хочет поменять местами две карточки (не обязательно соседние) так, чтобы все карточки с одинаковыми фруктами находились рядом друг с другом. Для какой из следующих ситуаций это сделать нельзя?

|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 33 - 1 = 32
|
В наборе карточек A) имеется ровно две карточки с яблоком. Они могут оказаться рядом, только если первую карточку (считая слева направо) поменять с одной из карточек с виноградом, или четвёртую карточку поменять с карточкой с вишней. В любом случае карточки с виноградом не окажутся рядом. Видим, что
за один шаг расположить нужным образом карточки нельзя. Значит, ответ А – правильный.
Хотя правильный ответ уже найден, нетрудно убедиться, что другие наборы карточек можно упорядочить так, как требуется, поменяв местами две карточки. Для этого нужно поменять местами карточки с номерами:
Б) 1 и 4; В) 2 и 4; Г) 3 и 5; Д) 3 и 4.
Задание 10
|
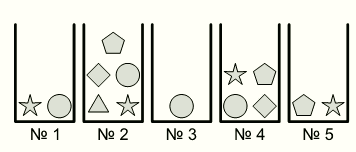
Соня хочет взять из пяти коробок 5 разных фигур. Из каждой коробки она может взять только одну фигуру. Какую фигуру она должна взять из коробки №4?
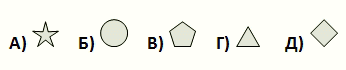
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 32 + 4 = 36
|
По условию, Соня должна взять пять фигурок из пяти коробок, но из каждой может взять только одну. Тогда она должна взять ровно по одной фигурке из каждой коробки. В коробке №3 нет других фигур, кроме кружочка. Поэтому взять кружочек Соня должна из коробки №3. Вычеркнем кружочки из всех коробок. Тогда в коробке №1 останется только звёздочка. Поэтому из коробки №1 Соня должна взять звёздочку. Вычеркнем звёздочки из всех коробок. Тогда в коробке №5 останется только пятиугольник. Поэтому именно его она должна взять из коробки №5. Вычеркнем из всех коробок пятиугольники. Тогда в коробке №4 останется только квадрат. Значит, только его Соня должна взять из этой коробки. В результате видим, что правильным является ответ Д.
По-другому правильный ответ можно найти так. В коробках имеется только 5 разных фигурок. Поэтому фигурку каждого вида Соня должна взять из какой-то коробки. Треугольник есть только в коробке №2. Поэтому из коробки №2 она должна взять треугольник. В частности, она не может взять из этой коробки квадрат. А его больше нет нигде, кроме коробки №4. Поэтому из коробки №4 Соня должна взять квадрат.
Задание 11
|
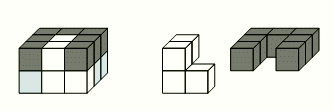
Блок на первом рисунке состоит из 18 кубиков трёх цветов: чёрного, белого и серого. Фигуры, образованные белыми кубиками и чёрными кубиками, показаны на рисунках справа. Как выглядит фигура, образованная серыми кубиками?

|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 36 - 1 = 35
|
Согласно условию задачи, блок состоит из 18 кубиков. На рисунке в условии видно, что среди этих 18 кубиков 4 белых и 7 чёрных кубиков. Поэтому число серых кубиков в блоке равно 18 – 4 – 7 = 7. Можно подсчитать, что фигуры в вариантах ответа состоят из:
А) 6; Б) 5; В) 6; Г) 6; Д) 7 кубиков.
Поэтому только ответ Д может быть правильным. И действительно, на рисунке в условии видим, что все серые кубики могут находиться только в нижнем слое блока и в этом слое два первых кубика в переднем ряду не серые. Поэтому серые – все остальные кубики нижнего слоя и, значит, они образуют именно такую фигуру, которая приведена в ответе Д.
Задание 12
|
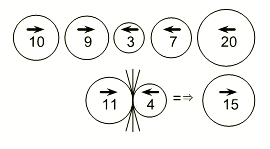
На рисунке изображены пять шаров, которые начинают двигаться одновременно с одной и той же скоростью в направлениях, указанных на них стрелками. Число, записанное на шаре, равно его весу. Когда два шара, двигавшихся в противоположных направлениях, сталкиваются, из них образуется больший шар, вес которого равен сумме весов столкнувшихся шаров. Образовавшийся шар продолжает двигаться в том же направлении, что и больший из столкнувшихся шаров (см. пример на рисунке). Каков окончательный результат столкновений данных пяти шаров?
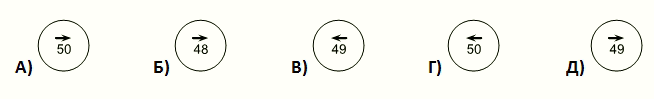
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 35 - 1 = 34
|
Результаты столкновения показаны ниже:
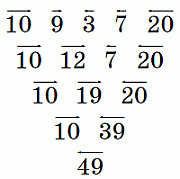
Задание 13
|
В магазине мороженого в ящике кассового аппарата находилась некоторая сумма денег. После продажи 6 мороженых в ящике стало 70 рублей. А после продажи в общей сложности 16 мороженых в ящике стало 120 рублей. Сколько рублей было в ящике первоначально?
A) 20 Б) 30 В) 40 Г) 50 Д) 60
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 34 - 1 = 33
|
По условию, после продажи 6 мороженых в ящике стало 70 рублей, а после продажи 16 мороженых в ящике стало 120 рублей. Видим, что в результате последней продажи 16 – 6 = 10 мороженых выручка увеличилась на 120 – 70 = 50 рублей. Это значит, что 10 мороженых стоят 50 рублей и, значит, одно мороженое стоит 5 руб. Тогда 6 мороженых стоят 6 · 5 = 30 рублей. Следовательно, до продажи 6 мороженых в кассе было 70 – 30 = 40 рублей.
Задание 14
|
Коала съел несколько листьев с трёх веток. На каждой ветке было по 20 листьев. Сначала он съел несколько листьев с первой ветки. Затем съел столько листьев со второй ветки, сколько осталось на первой. Наконец, он съел 2 листа с третьей ветки. Сколько всего листьев осталось на трёх ветках?
A) 20 Б) 22 В) 28 Г) 32 Д) 38
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 33 - 1 = 32
|
По условию, коала съел столько листьев со второй ветки, сколько их осталось на первой ветке. Тогда, если бы он съел такое же количество листьев не со второй, а с первой ветки, то с первой ветки он съел бы все листья, а на второй ветке все листья остались бы. Следовательно, с первых двух веток коала съел столько листьев, сколько было на одной ветке. То есть с первых двух веток он съел 20 листьев и 20 листьев осталось. Кроме того, согласно условию, на третьей ветке осталось 20 – 2 = 18 листьев. Поэтому всего на трёх ветках осталось 20 + 18 = 38 листьев.
Задание 15
|
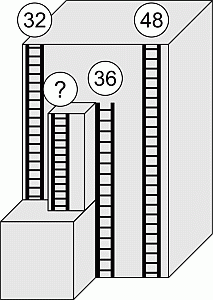
На здании расположены 4 пожарные лестницы, как показано на рисунке. Высоты трёх лестниц указаны над ними. Какова высота самой короткой лестницы?
A) 12 Б) 14 В) 16 Г) 20 Д) 22
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 32 - 1 = 31
|
Пронумеруем лестницы слева направо. Согласно данным на рисунке в условии задачи, высота здания равна длине четвёртой лестницы и, значит, равна 48. Тогда расстояние от верхушки третьей лестницы до крыши здания равно 48 – 36 = 12. Тогда и расстояние от верхушки второй лестницы до крыши также равно 12. Далее, рассмотрим первую лестницу. Согласно данным на рисунке, расстояние от земли до её нижней точки равно 48 – 32 = 16. Тогда и расстояние от земли до нижней точки второй лестницы также равно 16. Поэтому длина второй, самой короткой, лестницы равна 48 – 12 – 16 = 20.
По-другому ответ можно получить так. Заметим, что если совместить без смещения по вертикали первую и третью лестницы, то получим тот же результат, как если бы совместили вторую и четвёртую лестницы. Поэтому длина перекрытия при таких совмещениях, т.е.
длина второй самой короткой лестницы равна 32 + 36 – 48 = 20.
Задание 16
|

Нора играет с тремя чашками на кухонном столе. На каждом ходу она берёт самую левую чашку, переворачивает её и ставит справа от других чашек. На рисунке показан первый ход. Как будут расположены чашки после 10 таких ходов?

|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 31 - 1 = 30
|
Понятно, что после первых трёх ходов все три чашки будут перевёрнуты. Тогда ещё через три хода они все снова будут стоять правильно, как в начале. При этом всего будет сделано 3 + 3 = 6 ходов. Ещё через 3 хода (т.е. всего после 9 ходов) снова все три чашки будут перевёрнуты. Поэтому после 10-го хода правая чашка будет стоять правильно, а первые две останутся перевёрнутыми. Именно такое расположение чашек приведено в ответе Б.
Задание 17
|
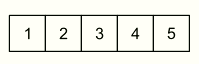
У Евы есть пять стикеров:  ,
,  ,
,  ,
, ,
,  . Она наклеила их в клетки полоски так, что
. Она наклеила их в клетки полоски так, что  находится не в клетке 5,
находится не в клетке 5,  – в клетке 1, а
– в клетке 1, а  – в клетке, соседней с клетками, в которых наклеены стикеры
– в клетке, соседней с клетками, в которых наклеены стикеры  и
и  . В какой клетке находится
. В какой клетке находится  ?
?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 5 = 35
|
По условию, яблоко находится в первой клетке, звёздочка – не в 5 клетке задачи. Кроме того, согласно условию, остальные три стикера расположены в трёх соседних клетках в виде
 или
или  .
.
Тогда расположение стикеров может быть только одним из двух возможных, указанных на рисунке.

Видим, что в обоих случаях цветок находится в клетке 4.
Задание 18
|

Семь карточек расположены так, как показано на рисунке. На каждой карточке записано по два числа, одно из которых перевёрнуто. Учитель хочет сделать так, чтобы сумма чисел в верхнем ряду была такой же, как сумма чисел в нижнем ряду. Ему достаточно перевернуть одну карточку. Какую?
A) A Б) C В) D Г) F Д) G
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 35 - 1.25 = 33.75
|
Сумма чисел на карточках в верхнем ряду равна
7 + 5 + 4 + 2+ 8 + 3 + 2 = 31,
в нижнем ряду равна
4 + 3 + 5 + 5 + 7 + 7 + 4 = 35
и, значит, сумма всех чисел равна 31 + 35 = 66. Поэтому, чтобы эти суммы уравнялись, они должны стать равными 66 : 2 = 33. Это значит, сумма чисел в верхнем ряду должна увеличиться на 33 – 31 = 2, а в нижнем – уменьшиться на 2. Поэтому нижнее число на искомой карточке должно быть на 2 больше верхнего числа. Разности между нижним и верхним числами на карточках следующие:
А) 4 − 7 = −3
В) 3 − 5 = −2
С) 5 − 4 = 1
D) 5 − 2 = 3
E) 7 − 8 = −1
F) 7 − 3 = 4
G) 4 − 2 = 2
Видим, что нужным свойством обладает только карточка G.
Задание 19
|
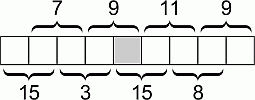
В клетки полоски вписали числа от 1 до 9. На рисунке указаны суммы чисел в некоторых парах соседних клеток. Какое число находится в серой клетке?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33.75 + 5 = 38.75
|
Первое решение.
Сумма всех девяти вписанных чисел равна
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.
А сумма всех чисел, кроме числа в первой клетке, согласно условию, равна
7 + 9 + 11 + 9 = 36.
Поэтому число в первой клетке равно
45 – 36 = 9.
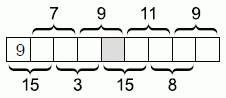
Тогда, так как сумма первых двух чисел равна 15, второе число равно 15 – 9 = 6; так как сумма второго и третьего числа равна 7, третье число равно 7 – 6 = 1. Далее, четвёртое число равно 3 – 1 = 2, пятое (искомое) число равно 9 – 2 = 7.
По-другому, можно было определить, что последнее число равно
45 – 15 – 3 – 15 – 8 = 4.
Далее, двигаясь справа налево, последовательно находить числа в клетках, пока не будет найдено число в серой клетке.
Второе решение.
Рассмотрим второе число (т.е. число во второй слева клетке). В сумме с первым числом оно даёт 15. Так как
все числа в полоске не больше 9, то второе число не меньше 15 – 9 = 6. В то же время сумма второго и третьего числа
равна 7, любое число в полоске не меньше 1. Поэтому второе число не
больше 7 – 1 = 6. Видим, что второе число может быть равно только 6. Более того, первые три числа – это соответственно 9, 6 и 1.
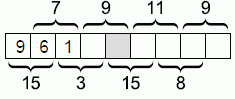
Тогда четвёртое число равно 3 – 1 = 2 и пятое (искомое) равно 9 – 2 = 7.
Задание 20
|
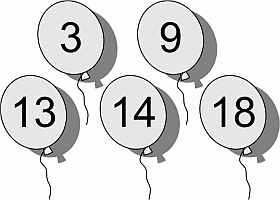
Мила бросала дротики в воздушные шары, за попадание в которые начислялись 3, 9, 13, 14 и 18 баллов. Всего она набрала 30 баллов. В шар какой стоимостью Мила уж точно попала?
A) 3 Б) 9 В) 13 Г) 14 Д) 18
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 38.75 - 1.25 = 37.5
|
Первое решение.
Мила заведомо попала хотя бы в один из шаров с баллами 13, 14, 18. В противном случае она набрала бы не более 9 + 3 = 12 баллов, а по условию она набрала 30 баллов.
Далее, если она попала в шар с 18 баллами, то ещё она должна была
попасть в шары с суммой баллов 30 – 18 = 12. Это возможно, но такую сумму дают только шары с 3 и 9 баллами. Если она попала в шар с 14 баллами, то ещё она должна была попасть в шары с суммой баллов 30 – 14 = 16. Это тоже возможно, но такую сумму дают только шары с 3 и 13 баллами. Если Мила попала в шар с 13 баллами, то ещё она должна была попасть в шары с суммой баллов 30 – 13 = 17. И это возможно, но такую сумму дают только шары с 3 и 14 баллами. Таким образом, Мила могла получить сумму 30 баллов только двумя способами:
18 + 9 + 3 = 30 или 14 + 13 + 3 = 30. Видим, что Мила наверняка попала в шар стоимостью 3 балла.
Второе решение.
Будем искать, в шары какой стоимости Мила могла не попасть. Сумма стоимостей всех шарах равна
3 + 9 + 13 + 14 + 18 = 57 баллов.
Поэтому Мила не попала в какие-то шары с суммой баллов 57 – 30 = 27. Сумму 27, учитывая стоимости всех шаров, можно получить только двумя способами: 18 + 9 = 27 или 14 + 13 = 27. Видим, что ни в одном из них нет шара стоимостью 3 балла. Следовательно, в шар стоимостью 3 балла Мила наверняка попала.
Задание 21
|
В коробке находится менее 50 конфет. Известно, что их можно разделить поровну между 2, 3 и 4 детьми. Однако их нельзя разделить поровну между 7 детьми – для этого понадобилось бы дополнительно еще 6 конфет. Сколько конфет в коробке?
A) 12 Б) 24 В) 30 Г) 36 Д) 48
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 37.5 - 1.25 = 36.25
|
Согласно условию, число конфет в коробке делится на 3 и на 4. (Вследствие делимости на 4 оно тем самым делится и на 2.) Поэтому число конфет в коробке делится на 3 • 4 = 12. Тогда в коробке могло быть 12, 24, 36 или 48 конфет. Кроме того, по условию,
если увеличить это число на 6, то полученное число должно делиться на 7. При таком увеличении получим числа 18, 30, 42 и 54, соответственно. Из них только число 42 делится на 7. Следовательно, в коробке было 42 – 6 = 36 конфет.
Задание 22
|

В пяти коробках находятся яблоки и бананы, в каждой коробке лежат фрукты только одного из видов. Общий вес всех бананов в 3 раза превышает вес всех яблок. В каких коробках находятся яблоки?
A) 1 и 2
Б) 2 и 3
В) 2 и 4
Г) 3 и 4
Д) 1 и 4
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 36.25 - 1.25 = 35
|
Согласно условию, общий вес всех фруктов в коробках равен
7 + 5+ 6 + 2 + 16 = 36.
При этом, если все яблоки из этих фруктов составляют одну часть, то все бананы составляют по весу три такие же части. Следовательно, яблоки по весу составляют четвёртую часть от всех фруктов. Поэтому они весят 9 кг. Среди данных коробок суммарный вес 9 кг имеют только коробки 1 и 4 (7 + 2 = 9). Поэтому правильным является ответ Д.
Задание 23
|
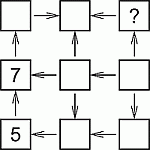
Лена хочет вписать числа от 1 до 9 в клетки на рисунке так, чтобы все стрелки были направлены от меньшего числа к большему. Она уже вписала числа 5 и 7. Какое число ей следует вписать в клетку со знаком вопроса?
A) 2 Б) 3 В) 4 Г) 6 Д) 8
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 35 - 1.25 = 33.75
|
От числа 7 можно перейти по стрелкам к двум числам в верхней строчке (сначала к числу в верхнем левом углу, а затем к числу, расположенному правее). Поэтому эти два числа больше 7 и, значит, равны соответственно 8 и 9 (см. рис.1).
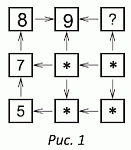
Далее, от четырёх чисел, отмеченных символом «*», можно перейти по стрелкам к числу 5. Следовательно, эти четыре числа меньше 5 и, значит, равны в каком-то порядке 1, 2, 3 и 4. Тогда для числа в клетке со знаком «?» остаётся единственное возможное значение – число 6.
Хотя ответ уже найден, приведём пример полной расстановки чисел в таблице (см. рис.2).
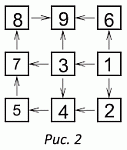
Ещё один пример, удовлетворяющий условию задачи, можно получить, если поменять местами числа 2 и 3.
Задание 24
|
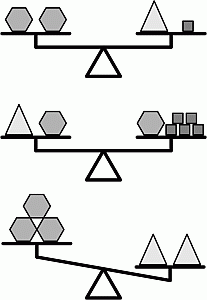
Мартин поместил на чаши весов предметы трёх разных видов: шестиугольники  , квадраты
, квадраты  и треугольники
и треугольники  . Что ему следует добавить на левую чашу третьих весов, чтобы их уравновесить?
. Что ему следует добавить на левую чашу третьих весов, чтобы их уравновесить?
A) 1 квадрат
Б) 2 квадрата
В) 1 шестиугольник
Г) 1 треугольник
Д) 2 треугольника
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
Будем измерять вес всех фигурок на
весах в квадратиках. Сбалансированность на вторых весах не нарушится, если с левой и с правой чаши снять шестиугольники. Следовательно, вес одного треугольника равен 5 квадратикам. Тогда, согласно результату на первых весах, два шестиугольника весят 5 + 1 = 6 квадратиков. Значит, один шестиугольник весит 3 квадратика. В результате на третьих весах имеем: вес предметов на левой чаше равен 3 • 3 = 9 квадратикам, а вес на правой чаше равен 2 • 5 = 10 квадратикам. Следовательно, чаши будут уравновешены, если на левую чашу положить 1 квадратик. Таким образом, правильным является ответ А.



 . Какой из следующих кубов она может из них сложить?
. Какой из следующих кубов она может из них сложить?













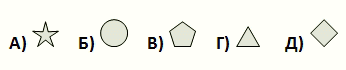


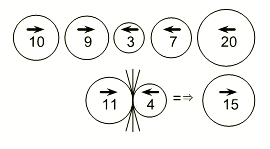
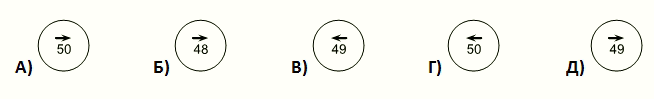
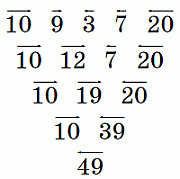



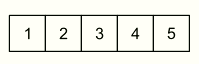
 ,
,  ,
,  ,
, ,
,  . Она наклеила их в клетки полоски так, что
. Она наклеила их в клетки полоски так, что  или
или  .
.




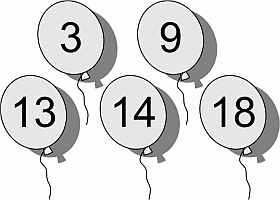





 , квадраты
, квадраты  и треугольники
и треугольники  . Что ему следует добавить на левую чашу третьих весов, чтобы их уравновесить?
. Что ему следует добавить на левую чашу третьих весов, чтобы их уравновесить?