Задание 1
|
Кенгуру выложил на стол 3 одинаковых палочки. Он их не гнул и не ломал. Какой из следующих результатов у него мог получиться?
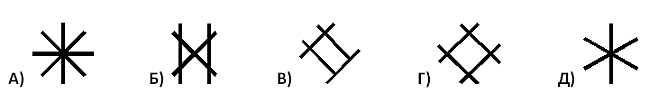
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 24 - 0.75 = 23.25
|
Можно увидеть, что в вариантах А-Г имеется по 4 палочки. Только в варианте Д их 3.
По-другому правильный ответ можно найти так. У каждой палочки ровно два конца. Поэтому у конструкции из 6 палочек должно быть 6 концов (если только палочки не соединены концами). Видим, что только конструкция в варианте Д имеет 6 концов. В других вариантах ответа 8 концов. Значит, ответ Д правильный
Задание 2
|
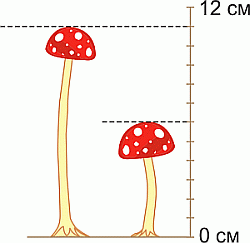
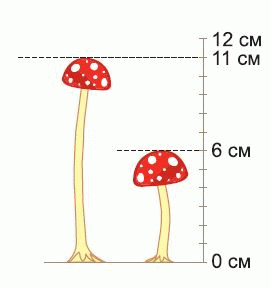
На рисунке показаны два мухомора. На сколько один из них выше другого?
A) 4 см Б) 5 см В) 6 см Г) 11 см Д) 17
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 23.25 - 0.75 = 22.5
|
Подсчёты на рисунке показывают, что высота первого мухомора равна 11 см, а высота второго - 6 см. Поэтому первый мухомор выше второго на 11-6 =5 см.
Задание 3
|
Какая из следующих линий на клетчатой бумаге самая длинная?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 22.5 + 3 = 25.5
|
Примем сторону клетки за 1 единицу и подсчитаем длины линий в вариантах ответа. Получим:

Видим, что наибольшую длину (15) имеет линия на рисунке А).
Задание 4
|
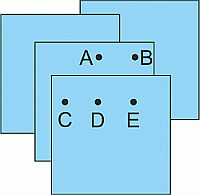
Четыре одинаковых листа бумаги расположены, как показано на рисунке. Миша хочет проткнуть их в какой-то точке так, чтобы образовались дырки на всех четырёх листах. В какой из следующих точек это нужно сделать?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 25.5 + 3 = 28.5
|
Дорисуем невидимые края данных четырёх листов.
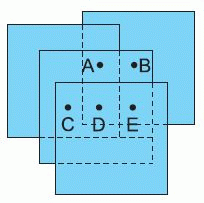
На полученном рисунке видим, что только точка D находится внутри всех четырёх листов. Следовательно, проткнуть листы нужно в точке D.
Задание 5
|

Элла надела футболку, изображённую на рисунке, и встала перед зеркалом. Какое изображение она может видеть в зеркале?
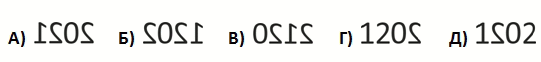
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 28.5 - 0.75 = 27.75
|
Надпись на футболке, записанная слева направо, в зеркале будет читаться справа налево. То есть первая цифра окажется последней, вторая – предпоследней
и т.д. Поэтому отразим симметрично число 2021 так, как показано на рисунке.
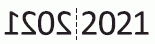
Сравним полученный результат с вариантами ответа. Видим, что правильным является ответ А.
Задание 6
|
Коричневая башня выше красной, но ниже зелёной. Серебряная башня выше зелёной. Какая башня самая высокая?
A) коричневая
Б) зелёная
В) красная
Г) серебряная
Д) невозможно определить
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 27.75 + 3 = 30.75
|
По условию, коричневая башня выше красной, но ниже зелёной, а серебряная – выше зелёной. Изобразим это схематично (см. рис.).
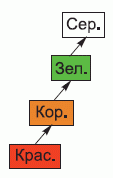
Видим, что самой высокой является серебряная башня.
Задание 7
|

Дети стоят в ряд, как показано на рисунке. Некоторые смотрят вперед, другие – назад. Сколько из них держат за руку другого ребенка правой рукой?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 30.75 - 0.75 = 30
|
Пятеро детей держат руками двоих детей. В частности, каждый из них держит кого-то правой рукой. Ещё правой рукой держит соседнего мальчика девочка, которая на рисунке стоит крайней справа. Всего правой рукой держат кого-то рядом стоящего 6 детей.
Задание 8
|
В созвездии Кенгуру каждой звезде присвоено некоторое своё число, большее 3. Сумма всех чисел равна 20. На каком из следующих рисунков показано созвездие Кенгуру?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30 + 3 = 33
|
Только в созвездии Б) все числа на звёздах больше 3 (см. рис. в условии задачи). Сумма чисел на звёздах в этом созвездии, как и требуется в условии, равна 8 + 7 + 5 = 20. Следовательо, созвездие Кенгуру показано на рисунке Б).
Задание 9
|
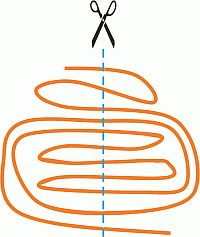
Эдик разрезал ленту, как показано на рисунке. Сколько кусков ленты у него получилось?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 33 - 1 = 32
|
Чтобы найти число кусков, совсем не обязательно пересчитывать их непосредственно. Заметим, что после каждого разреза ленты или её части число кусков увеличивается на 1. Всего лента разрезана в 11 местах (см. рис.).
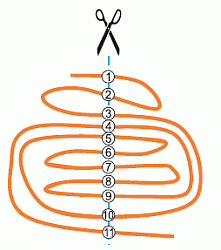
Следовательно, в результате разрезаний число кусков ленты увеличилось с 1 до 1 + 11 = 12.
Задание 10
|
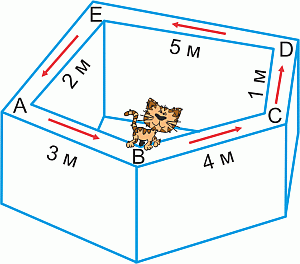
Кот ходит по стене в направлении стрелок, как показано на рисунке. Он начал путь в точке B и прошёл 20 метров. В какой точке он оказался?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 32 - 1 = 31
|
Полный круговой обход стены составляет
4 + 1 + 5 + 2 + 3 = 15 метров (см. рис. в условии задачи).
Поэтому, пройдя 15 м, кот вернулся в исходную точку B. Пройдя ещё 20 – 15 = 5 м, он оказался в точке D.
Задание 11
|

У Юли есть два горшка с цветами, они изображены на рисунке. Юля хочет купить ещё несколько цветков и посадить их в эти горшки так, чтобы цветков каждого вида в одном горшке было столько же, сколько в другом горшке. Какое наименьшее количество цветков Юле нужно купить?
A) 2 Б) 4 В) 6 Г) 8 Д) 10
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 31 - 1 = 30
|
В первом горшке 2 белых цветка, а во втором таких цветков 4. Поэтому Юле необходимо в первый горшок посадить по крайней мере 4 – 2 = 2 белых цветка. Далее, в первом горшке 4 серых цветка, а во втором их только 1. Поэтому Юле необходимо во второй горшок посадить по крайней мере 4 – 1= 3 серых цветка. Наконец, в первом горшке 2 чёрных цветка, а во втором 3 таких цветка. Поэтому
Юле необходимо в первый горшок посадить по крайней мере 3 – 2 = 1 такой цветок. Видим, что Юле необходимо купить по крайней мере 2 + 3 + 1 = 6 цветков. С другой стороны, если Юля купит 2 белых, 3 серых и 1 чёрный цветок и посадит их в соответствующие горшки, то
в горшках цветов каждого вида станет поровну. Следовательно, правильным является ответ 6.
Задание 12
|

Том кодирует слова, используя таблицу на рисунке. Например, слово PIZZA имеет код A2, A4, C1, C1, B2. Какое слово Том закодировал как B3, B2, C4, D2?
A) MAZE Б) MASK В) MILK Г) MATE Д) MATH
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 30 - 1 = 29
|

Буквы, закодированные как B3, B2, C4, D2, выделены в таблице. Их запись в соответствующем порядке образует слово MATH.
Задание 13
|
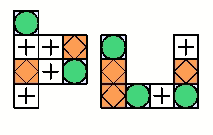
Какой из следующих квадратов можно сложить из двух данных частей на рисунке?
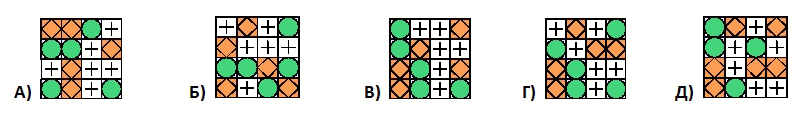
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 29 - 1 = 28
|
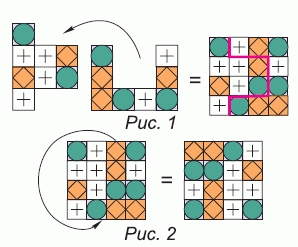
Повернём вторую фигуру на четверть оборота, как показано на рисунке 1 и соединим с первой фигурой. Получим квадрат, изображённый в правой части этого рисунка. При непосредственном сравнении полученный квадрат не совпадает ни с одним в вариантах
ответа. Поэтому будем его поворачивать и
сравнивать с вариантами ответа. На рисунке 2 показано, что при повороте построенного квадрата на пол-оборота его изображение совпадёт с квадратом в варианте ответа А. Этот ответ и является правильным.
Задание 14
|
Юля и Анжела играли в «кенгбол» – игру с мячом. Каждый гол в этой игре приносит 2 очка. Юля забила 5 голов, а Анжела – 9 голов. На сколько очков больше набрала Анжела, чем Юля?
A) 4 Б) 6 В) 8 Г) 10 Д) 12
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 28 - 1 = 27
|
Согласно условию, в ходе игры Юля набрала 5 • 2 = 10 очков, а Анжела набрала 9 • 2 = 18 очков. Видим, что Анжела набрала на 18 – 10 = 8 очков больше.
Задание 15
|
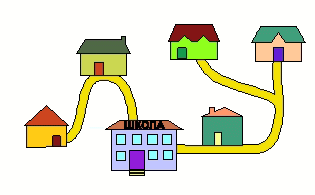
На рисунке изображены пять домов пяти друзей и их школа. Школа – самое большое здание на рисунке. Даша и Оля по пути в школу проходят мимо дома Лёши, а путь Евы проходит мимо дома Коли. Какой из домов – дом Евы?
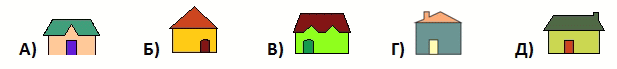
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 27 - 1 = 26
|
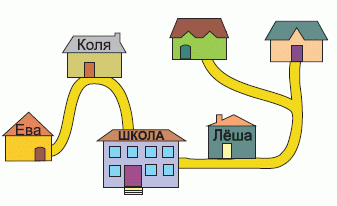
Из условия следует, что дома Лёши и Коли – не крайние и однозначно те, которые указаны на рисунке. А тогда дом Евы – самый левый на рисунке, т. е. тот, который указан в ответе Б.
Задание 16
|
На обед у кенгуру было две ветки, на каждой ветке по 10 листьев. Кенгуру съел несколько листьев с первой ветки. Потом со второй ветки он съел столько листьев, сколько осталось на первой ветке. Сколько всего листьев осталось на двух ветвях?
A) 5 Б) 6 В) 8 Г) 10 Д) 15
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 26 - 1 = 25
|
Согласно условию, кенгуру со второй ветки съел столько листьев, сколько осталось на первой ветке. Получается, что если бы он съел столько же листьев не со второй, а с первой ветки, то на первой ветке не осталось бы листьев. Выходит, что кенгуру съел столько листьев, сколько было на первой ветке. Значит, осталось столько листьев, сколько их было на второй ветке, т. е. осталось 10 листьев.
Задание 17
|
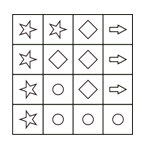
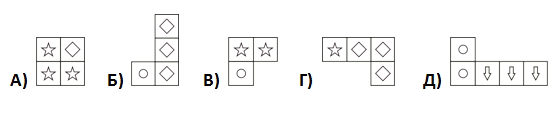
Маша сложила изображённый на рисунке квадрат из каких-то четырёх фигур в вариантах ответа. Какой фигурой она не воспользовалась?
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 25 - 1.25 = 23.75
|
Стрeлки имеются только у фигуры Д). Поэтому её Маша точно использовала для построения квадрата. Далее, в построенном квадрате имеется 5 звёздочек. Столько звёздочек в сумме имеют только фигуры А) и В). Следовательно, фигура Г), которая также имеет звёздочку, является лишней. Соответствующее построение приведено на рисунке.

Задание 18
|
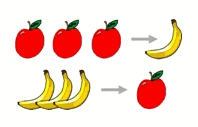
Каждый раз, когда у Бабы Яги есть 3 яблока, она превращает их в 1 банан, а когда у неё есть 3 банана, она превращает их в 1 яблоко. Что у неё получится в результате, если вначале будет 4 яблока и 5 бананов?

|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 23.75 - 1.25 = 22.5
|
Первое превращение определяется неоднозначно. Есть две возможности: либо Баба Яга сначала превратила 3 яблока в 1 банан, либо 3 банана – в 1 яблоко. Но далее в каждом из этих двух случаев все следующие превращения определены однозначно. Они показаны в таблицах.
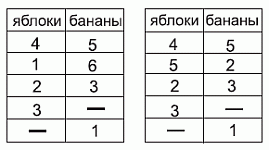
Видим, что в результате в обоих случаях остаётся 1 банан.
Задание 19
|
Карточки  поместили в две коробки. Суммы чисел на карточках в обеих коробках оказались одинаковыми. Какое из следующих чисел должно оказаться в одной и той же коробке с числом 4?
поместили в две коробки. Суммы чисел на карточках в обеих коробках оказались одинаковыми. Какое из следующих чисел должно оказаться в одной и той же коробке с числом 4?
A) только 3
Б) только 5
В) только 6
Г) 5 или 6
Д) невозможно определить
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 22.5 - 1.25 = 21.25
|
Сумма чисел на всех карточках равна
2 + 3 + 4 + 5 + 6 = 20.
Поэтому сумма чисел на карточках в одной коробке должна быть равна 20 : 2 = 10. Тогда в коробке с числом 4 должны находиться
карточки (или одна карточка), сумма чисел на которых равна 10 – 4 = 6.
Среди чисел 2, 3, 5, 6 таким является только одно число – число 6. Поэтому только число 6 должно оказаться в одной коробке с числом 4.
Задание 20
|

На рисунке показаны две шестерёнки, каждая с одним чёрным зубом. Как будут расположены чёрные зубья после того, как маленькая шестерёнка сделает один полный оборот?

|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 21.25 - 1.25 = 20
|
Маленькая шестерёнка имеет 8 зубьев. Поэтому если она совершит полный поворот, т. е. поворот на 8 зубьев, по ходу часовой стрелки,
то большая шестерёнка тоже совершит поворот на 8 зубьев, но против хода часовой стрелки. Таким образом, чёрный зуб повернётся на 8 позиций против хода часовой стрелки (см. рис.).
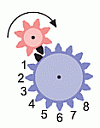
Видим, что он займёт такое положение, которое указано в ответе В.
Задание 21
|
Три девочки и два мальчика танцевали друг с другом. Они танцевали парами так, что каждая девочка танцевала с каждым мальчиком ровно одну минуту. В любой момент времени на танцплощадке была только одна пара. Сколько всего минут танцевали дети?
A) 5 Б) 6 В) 8 Г) 9 Д) 10
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 20 - 1.25 = 18.75
|
Согласно условию, каждая из трёх девочек танцевала с двумя мальчиками, по 1 минуте с каждым, т. е. ровно 2 минуты. Поэтому в сумме все три девочки танцевали 3 · 2 = 6 минут. А так как они танцевали по очереди и других танцев не было, то танцы продолжались 6 минут.
Задание 22
|
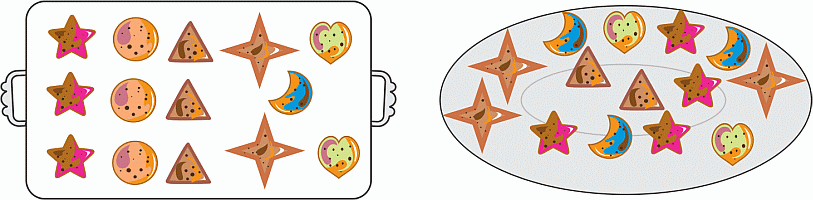
Каждый участник кулинарного конкурса испёк одинаковый набор печений. Поднос с таким набором печений показан на первом рисунке. Какое наименьшее количество таких подносов нужно, чтобы из имеющихся на них печений можно было составить набор, показанный на втором рисунке?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 18.75 - 1.25 = 17.5
|
Заметим, что на тарелке на втором рисунке в условии задачи находятся 3 печенья в форме полумесяца. На подносе – только 1 такое печенье. Поэтому понадобятся не менее чем 3 данных подноса. С другой стороны, легко видеть, что 3 подноса (даже 2) достаточно, чтобы собрать на тарелке нужные количества печений других видов. Поэтому правильным является ответ 3.
Задание 23
|
Кенга ест только яблоки в понедельник, среду и пятницу. По вторникам и четвергам он ест только манго. По субботам и воскресеньям он ничего не ест. В день он съедает либо 2 яблока, либо 3 манго. Сколько всего фруктов съедает Кенга за две недели?
A) 12 Б) 16 В) 18 Г) 20 Д) 24
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 17.5 - 1.25 = 16.25
|
Согласно условию, в понедельник, среду и пятницу Кенга съедает по 2 яблока. Всего за эти 3 дня он съедает 2 + 2 + 2 = 6 яблок. Далее, по вторникам и четвергам Кенга съедает по 3 манго. Всего за эти 2 дня он съедает 3 + 3 = 6 манго. В другие дни недели Кенга ничего не ест. Видим, что за неделю Кенга съедает 6 + 6 = 12 фруктов. Тогда за 2 недели он съедает 12 + 12 = 24 фрукта.
Задание 24
|
У Стёпы есть пять игрушек: мяч, набор кубиков, конструктор, пазл и машинка. Каждую игрушку он поместил на отдельную полку книжного шкафа. Мяч оказался выше кубиков, но ниже машинки. Конструктор Стёпа положил непосредственно над мячом. На какой полке не мог оказаться пазл?
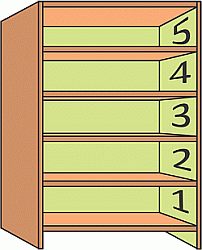
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 16.25 - 1.25 = 15
|
Согласно условию, конструктор и мяч оказались на соседних полках. Но они не могут быть на двух самых верхних полках, так выше их расположена машинка. Они не могут быть и на двух самых нижних полках, так как ниже их расположены кубики. Поскольку конструктор и мяч не могут занимать полки 1 и 5, то они
могут находиться только либо на 2 и 3 полке, либо на 3 и 4 полке. Видим, что в обоих случаях они занимают полку 3. Следовательно, пазл не может находиться на полке 3.
Хотя правильный ответ уже найден, отметим, что на любой другой полке пазл оказаться мог.



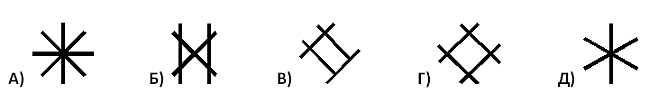







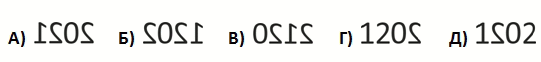
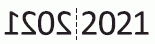









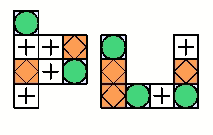
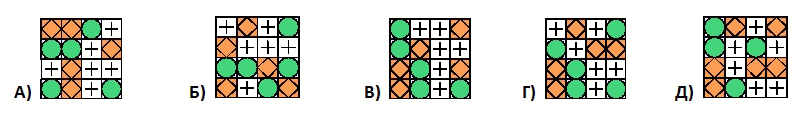


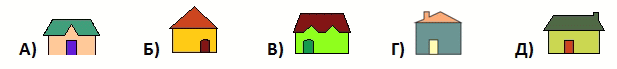







 поместили в две коробки. Суммы чисел на карточках в обеих коробках оказались одинаковыми. Какое из следующих чисел должно оказаться в одной и той же коробке с числом 4?
поместили в две коробки. Суммы чисел на карточках в обеих коробках оказались одинаковыми. Какое из следующих чисел должно оказаться в одной и той же коробке с числом 4?




