Задание 1
|
Сколько простых чисел среди чисел 2, 20, 202 и 2020?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30 + 3 = 33
|
Число называется простым, если имеет ровно два делителя (1 и само это число). Среди чисел 2, 20, 202 и 2020 таким свойством обладает только число 2. Поэтому правильным является ответ 1.
Задание 2
|
У какого из следующих правильных многоугольников отмеченный угол является наибольшим?

|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Как известно, угол правильного треугольника равен 60°, а угол квадрата равен 90°. Выпуклый пятиугольник можно разбить на 3 треугольника, а выпуклый шестиугольник – на 4 треугольника (см. рис.).
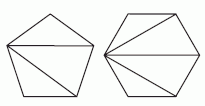
А так как сумма углов треугольника равна 180°, то сумма углов выпуклого пятиугольника равна 180° · 3 = 560°, а сумма углов выпуклого шестиугольника равна 180° · 4 = 720°. Поэтому угол правильного пятиугольника равен 540° : 5 = 108°, а угол правильного шестиугольника равен 720° : 6 = 120°. Видим, что наибольшим среди данных углов является угол шестиугольника, изображённого в ответе А.
Вообще говоря, несложно доказать, что угол правильного n-угольника равен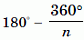 . Из этой формулы видно, что чем больше n, тем больше данный угол.
. Из этой формулы видно, что чем больше n, тем больше данный угол.
Задание 3
|
Миша, готовясь к олимпиаде, решает 6 задач каждый день, а Лиза – 4 задачи каждый день. Сколько дней понадобится Лизе, чтобы решить столько же задач, сколько решит Миша за 4 дня?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Согласно условию, за 4 дня Миша решит 4 · 6 = 24 задачи. Тогда Лизе, чтобы решить столько же задач, понадобится 24 : 4 = 6 дней.
Задание 4
|
Какая из следующих дробей имеет наибольшее значение?
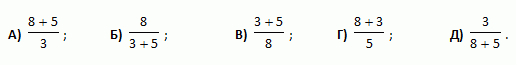
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Имеем:
А) 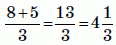
Б) 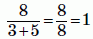
В) 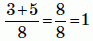
Г) 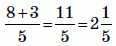
Д) 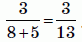
Видим, что наибольшей является дробь в варианте А
Задание 5
|

Большой квадрат разбит на меньшие квадраты так, как показано на рисунке. А один из квадратов ещё разбит диагональю на два треугольника. Какая по площади часть большого квадрата является серой?
A) 4/5 Б) 3/8 В) 4/9 Г) 1/3 Д) 1/2
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
На рисунке в условии задачи видно, что равных фигур серого и белого цвета имеется поровну: по одному большому квадрату в нижней части рисунка, по одному треугольнику в правой верхней части и по два малых квадрата в левой верхней части. Поэтому серая и белая части исходного квадрата имеют равные
площади. Следовательно, правильным является ответ Д.
Задание 6
|
В футбольном турнире участвуют 4 команды. Каждая команда должна сыграть с каждой один матч. В каждом матче победитель получает 3 очка, а проигравший – 0 очков. В случае ничьей обе команды получают по 1 очку. Какое из следующих чисел не может быть суммой очков, набранных какой-нибудь командой после завершения турнира?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33.75 + 3 = 36.75
|
В данном турнире каждая команда должна сыграть 3 матча. Если какая-то команда все матчи выиграет, то она наберёт
3 + 3 + 3 = 9 очков.
Если же она хотя бы один матч не выиграет, то наберёт не более
3 + 3 + 1 = 7.
Видим, что 8 очков команда набрать не может. Поэтому правильным
является ответ Д.
Заметим дополнительно, что в данном турнире команда может набрать любое количество очков от 0 до 9, кроме 8.
Задание 7
|
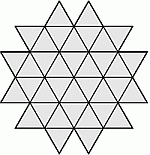
Петя сложил из 36 одинаковых треугольных плиток фигуру на рисунке. Какое наименьшее количество таких плиток ещё нужно добавить, чтобы эта фигура превратилась в шестиугольник?
A) 10 Б) 12 В) 15 Г) 18 Д) 24
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 36.75 + 3 = 39.75
|
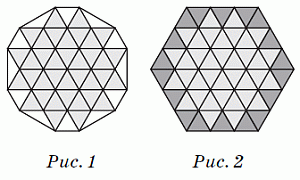
Рассмотрим выпуклую оболочку данной фигуры, т.е. наименьшую выпуклую фигуру, которая содержит данную фигуру (см. рис.1). Она не является шестиугольником, и её граница состоит из чередующихся коротких и длинных отрезков. Чтобы получить правильный шестиугольник, каждый из этих отрезков надо покрыть данными треугольными плитками так, чтобы они примыкали к сторонам данной фигуры. Короткий отрезок, очевидно, равен стороне плитки и покрывается одной плиткой (одной из его сторон). Но длинный отрезок длиннее стороны плитки и, значит, может быть покрыт не менее чем двумя плитками. Весь периметр выпуклой оболочки состоит из 6 коротких и 6 длинных отрезков. Поэтому, чтобы все их покрыть, необходимо не менее
6 · 1 + 6 · 2 = 18 плиток.
С другой стороны, если добавить к данной фигуре 18 плиток так, как показано на рисунке 2, то получится шестиугольник. Таким образом, правильным является ответ 18.
Задание 8
|
Ванда хочет перемножить какие-то три различных числа из чисел –5, –3, –1, 2, 4 и 6. Какой наименьший результат она может получить?
A) –200 Б) –120 В) –90 Г) –48 Д) -15
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 39.75 + 3 = 42.75
|
Некоторые из произведений могут быть отрицательными. Поэтому наименьшим будет произведение трёх чисел с наибольшими возможными модулями, среди которых одно или три числа отрицательные. Легко видеть, таким произведением является произведение
–5 · 4 · 6 = –120.
Задание 9
|
Если Женя едет в школу на автобусе, а затем идёт назад пешком, то на дорогу туда и обратно у него уходит 3 часа. А если он едет на автобусе в обе стороны, то он находится в дороге 1 час. Сколько времени понадобится Жене, если он до школы и обратно будет идти пешком?
A) 3,5 часа Б) 4 часа В) 4,5 часа Г) 5 часов Д) 5,5 часа
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 42.75 - 0.75 = 42
|
Так как на дорогу от дома до школы и обратно на автобусе у Жени уходит 1 час, то на дорогу в одну сторону ему нужно 0,5 часа. Тогда, согласно условию, на дорогу в одну сторону пешком у Жени уходит 3 – 0,5 = 2,5 часа. Следовательно, на дорогу в обе стороны пешком Жене нужно 2,5 · 2 = 5 часов.
По-другому эту задачу можно было решить так. Из условия следует, что у Жени на дорогу в одну сторону пешком уходит на 3 – 1 = 2 часа больше, чем на автобусе. Поэтому на дорогу в обе стороны пешком ему нужно 3 + 2 = 5 часов.
Можно было рассуждать и так. Если Женя дважды поедет в школу на автобусе и будет возвращаться пешком, то у него на это уйдёт 3 + 3 = 6 часов. При этом он дважды проедет на автобусе расстояние между домом и школой (на что ему нужен 1 час) и дважды пройдёт его пешком. Поэтому на дорогу в обе стороны пешком Жене нужно 6 – 1 = 5 часов.
Задание 10
|
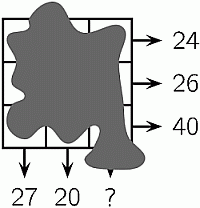
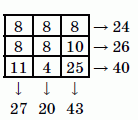
В каждой клетке таблицы 3 × 3 было записано число. К сожалению, таблица оказалась залита чернилами так, что ни одного числа не стало видно. Но суммы чисел в строчках и двух столбцах известны (см. рис.). Чему равна сумма чисел в третьем столбце?
A) 41 Б) 43 В) 44 Г) 45 Д) 47
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 42 - 0.75 = 41.25
|
Если сложить суммы чисел во всех трёх строчках, то получим сумму всех чисел в таблице. Согласно условию, она равна
24 + 26 + 40 = 90.
Если сложить сумму во всех трёх столбцах, то мы тоже получим сумму всех чисел в таблице, которая, как мы уже
знаем, равна 90. Поэтому сумма чисел в третьем столбце равна
90 – 27 – 20 = 43.
Заметим, что примеров таблиц, удовлетворяющих условию задачи, существует бесконечно много. Один из них показан ниже. Но для решения задачи приводить пример не обязательно.
Задание 11
|
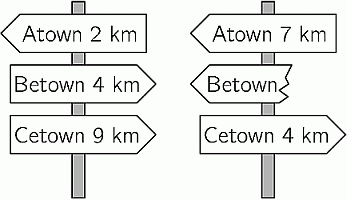
Кратчайший путь от Атауна до Цетауна пролегает через Бетаун. Два указателя показаны на этом пути. Какое расстояние было написано на сломанном знаке?
A) 1 км Б) 3 км В) 4 км Г) 5 км Д) 9 км
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 41.25 - 1 = 40.25
|
Согласно данным на первом указателе, расстояние между Атауном и Бетауном равно 2 + 4 = 6 км. Тогда, согласно данным на втором указателе, расстояние от него до Бетауна равно 7 – 6 = 1 км. Это расстояние и должно было быть написано на утерянной части второго указателя.
По-другому этот результат можно было получить так. Согласно данным на первом указателе, расстояние между Бетауном и Цетауном равно 9 – 4 = 5 км. Тогда, согласно данным на втором указателе, расстояние от него до Бетауна равно 5 – 4 = 1 км.
Задание 12
|
Анна хочет в марте гулять в среднем 5 км каждый день. 16 марта, перед тем как лечь спать, она подсчитала, что до сих пор она прошла 95 км. Какое расстояние ей нужно в среднем проходить за оставшиеся дни марта для достижения своей цели?
A) 5,4 км Б) 5 км В) 4 км Г) 3,6 км Д) 3,1 км
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 40.25 - 1 = 39.25
|
В марте 31 день. Поэтому, если Аня хочет в этом месяце проходить в среднем 5 км в день, то в течение месяца ей нужно пройти 31 · 5 = 155 км. По условию, за первые 16 дней она прошла 95 км. Тогда за оставшиеся 31 – 16 = 15 дней ей остаётся пройти 155 – 95 = 60 км. Это означает, что в оставшиеся дни ей в среднем нужно проходить 60 : 15 = 4 км в день.
Задание 13
|
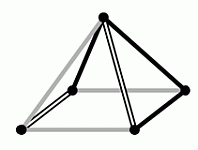
Как выглядит следующая пирамида, если посмотреть на неё сверху?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 39.25 + 4 = 43.25
|
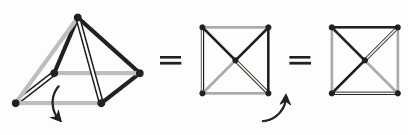
Повернём пирамиду вокруг переднего ребра основания так, чтобы в плоскости листа получить вид сверху (см. рис.). Затем повернём полученный вид сверху вокруг центра против часовой стрелки на 90°. Видим, что результат
совпадает с ответом Б.
Задание 14
|
Каждый ученик в классе занимается либо плаванием, либо танцами, либо и тем, и другим. Три пятых учеников класса занимаются плаванием и столько же – танцами. Пять учеников класса занимаются и плаванием, и танцами. Сколько учеников в этом классе?
A) 15 Б) 20 В) 25 Г) 30 Д) 35
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 43.25 - 1 = 42.25
|
Если сложить три пятых учеников класса (подразумевая тех, кто занимается плаванием) и три пятых (подразумевая тех, кто занимается танцами), то получим шесть пятых класса, что на одну пятую больше всех учеников класса. При этом учтены все ученики класса, но те из них, кто занимается и плаванием, и танцами, учтены дважды. По условию, в классе число таких учеников равно 5. Следовательно, 5 – это одна пятая от числа всех учеников класса и, значит, всего в классе 5 · 5 = 25 учеников.
По-другому ответ можно было получить так. Пусть в классе n учеников. Тогда среди них 3/5 n занимаются плаванием и столько же занимаются танцами. Но 5 учеников занимаются и плаванием, и танцами. Поэтому 3/5 n - 5 учеников занимаются только плаванием и 3/5 n - 5 занимаются только танцами. Подсчитывая по частям число учеников класса, получаем уравнение
(3/5 n - 5) + (3/5 n - 5) + 5 = n,
решая которое, находим n = 25.
Задание 15
|
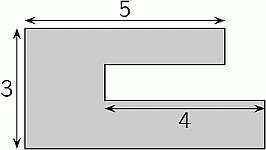
Дедушкин сад имеет форму, показанную на рисунке. Все его стороны параллельны или перпендикулярны друг другу. Некоторые размеры указаны на рисунке. Каков периметр дедушкиного сада?
A) 22 Б) 23 В) 24 Г) 25 Д) 26
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 42.25 + 4 = 46.25
|
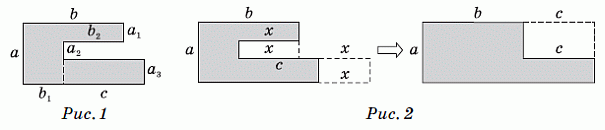
Решим задачу в общем виде. Обозначим участки периметра сада, заданные в условии задачи, через a, b и c (см. рис.1). Обозначим также неизвестные участки периметра так, как показано на этом рисунке. Тогда легко видеть, что
a1 + a2 + a3 = a и b1 + b2 = b.
Поэтому периметр сада равен
2(a + b + c).
При a = 3, b = 5 и c = 4 значение периметра равно
2(3 + 5 + 4) = 24.
По-другому получить ответ можно, перестроив фигуру сада так, чтобы её периметр не изменился и чтобы вычисления периметра полученной фигуры стали очевидными. Это можно сделать, например, так, как показано на рис.2. Видим, что в результате получился прямоугольник со сторонами a и b + c. Его периметр равен
2(a + b + c).
Задание 16
|
У Эндрю есть 27 одинаковых маленьких кубиков, у каждого две смежные грани окрашены в красный цвет, остальные грани – белые. Эндрю построил из всех кубиков большой куб. Какое наибольшее количество полностью красных граней может иметь построенный куб?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 46.25 - 1 = 45.25
|
Рассмотрим угловой кубик построенного куба. Для определённости, пусть он находится на пересечении передней, верхней и правой грани.

Так как, по условию, у этого кубика (как и у всех) ровно две грани красные, то и у построенного куба из трёх граней, в углу которых находится данный кубик, не более чем две грани могут быть полностью красными. На рисунке это передняя и верхняя грани. При этом правая грань не может быть полностью красной. Ясно также, что если указанные грани полностью красные, то и левая грань не является полностью красной. Таким образом, из шести граней построенного куба не более четырёх граней могут быть полностью красными. А четыре полностью красные грани, легко видеть, у построенного куба могут получиться. Можно сделать так, что, помимо верхней и передней граней, на данном рисунке красными будут нижняя и задняя грани. Таким образом, правильным является ответ 4.
Задание 17
|
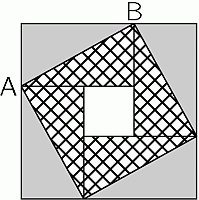
Большой квадрат состоит из четырёх одинаковых прямоугольников и небольшого квадрата в центре. Площадь большого квадрата равна 49 см2, а длина диагонали AB одного из прямоугольников равна 5 см. Какую площадь имеет небольшой квадрат в центре?
A) 1 см2
Б) 2,25 см2
В) 4 см2
Г) 9 см2
Д) 16 см2
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 45.25 - 1 = 44.25
|
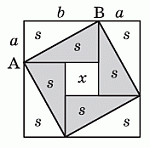
Согласно условию, данный квадрат площади 49 см2 состоит из 8 равных прямоугольных треугольников и центрального квадрата, площадь которого нужно найти. Пусть эта площадь равна x, а площади треугольников равны s. Тогда
8s + x = 49. (1)
Далее, легко видеть, что 4 серых треугольника и квадрат в центре также образуют квадрат. По условию, его сторона AB = 5 см, и, значит, его площадь равна 52 = 25 см2. Поэтому имеем:
4s + x = 25. (2)
Умножим на 2 равенство (2) и вычтем из результата равенство (1). Получим
2(4s + x) – (8s + x) = 2 · 25 – 49,
или, после упрощения, x = 1. Таким образом, площадь центрального квадрата
равна 1 см2.
По-другому ответ можно было получить с помощью теоремы Пифагора. Если обозначить катеты рассматриваемых треугольников через a и b, то, согласно этой теореме, a2 + b2 = AB2, т.е., согласно условию, a2 + b2 = 25.
Далее, видим, что сторона данного большого квадрата равна a + b. Согласно условию,
(a + b)2 = 49, или a2 + b2 +2ab = 49,
откуда 2ab = 24. Но 2ab = 4s, где s – площадь одного треугольника. Поэтому 4s = 24, т.е. серая часть квадрата со стороной AB = 5 см равна 24 см2. Поэтому площадь квадрата в центре
x = 25 – 24 = 1 см2.
Задание 18
|
Зарплата Вернера составляет 20% от зарплаты его босса. На сколько процентов нужно увеличиваться зарплату Вернера, чтобы она стала равна зарплате его босса?
A) 80% Б) 120% В) 180% Г) 400% Д) 500%
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 44.25 - 1 = 43.25
|
По условию, зарплата Вернера составляет 20% от зарплаты его босса. Это означает, что его зарплата в 5 раз меньше зарплаты босса. Поэтому, чтобы зарплата Вернера стала равна зарплате босса, нужно увеличить её в 5 раз. После этого она будет составлять 500% от исходной, т.е. будет больше её на 400%. Таким образом, правильным является ответ 400%.
По-другому решение можно получить так. Пусть зарплата босса равна x. Тогда зарплата Вернера равна 0,2x. Для того, чтобы она стала равна x, её надо увеличить на x – 0,2x = 0,8x, т.е. на 0,8x/0,2x · 100% = 400%.
Задание 19
|
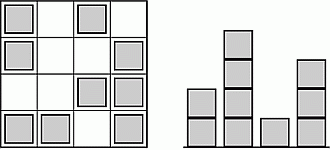
Ирина построила «город» из одинаковых кубиков. На первом из следующих рисунков показан вид «города» сверху, а на втором – вид с одной из сторон, но неизвестно, с какой. Какое наибольшее количество кубиков Ирина могла использовать для построения «города»?
A) 25 Б) 24 В) 23 Г) 22 Д) 21
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 43.25 - 1 = 42.25
|
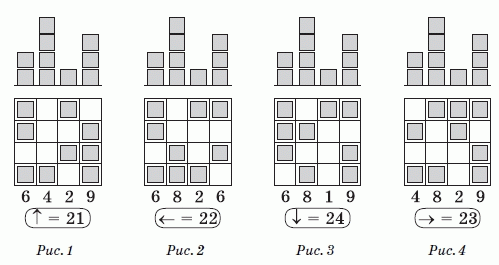
Поскольку неизвестно, с какой стороны дан вид «города» на втором рисунке в условии задачи, по очереди рассмотрим все четыре варианта, поворачивая квадрат на первом рисунке. Если смотреть на город с юга (т.е. на первый рисунок снизу; рис.1), то видим, что в основании города в первом столбце слева находятся 3 блока с максимальной высотой 2 кубика. Поэтому наибольшее общее количество кубиков в этом столбце равно 3 · 2 = 6. Во втором столбце в основании только 1 блок высотой 4 кубика, всего в этом столбце имеется 1 · 4 = 4 кубика. В третьем столбце в основании 2 блока высотой 1 кубик, всего в этом столбце 2 · 1 = 2 кубика. В четвёртом столбце в основании 3 блока максимальной высоты 3 кубика, наибольшее число кубиков в этом столбце равно 3 · 3 = 9. В результате, в этом случае наибольшее
число кубиков «города» равно
6 + 4 + 2 + 9 = 21.
Аналогичные вычисления для вида города с востока (справа; рис.2), с севера (сверху; рис.3) и с запада (слева; рис.4) дают соответственно значения 22, 24 и 23. Таким образом, наибольшее количество кубиков, которое Ирина могла использовать для построения «города», равно 24.
Задание 20
|

У Маши есть полоска бумаги, разбитая на клетки с числами 1, 2, 3, 4 и 5 в клетках (см. рис.). Она складывает полоску разными способами так, что клетки накрывают друг друга в 5 слоёв. В каком порядке (от верхнего слоя к нижнему) не могут располагаться числа в клетках сложенной полоски?
A) 3, 5, 4, 2, 1
Б) 3, 4, 5, 1, 2
В) 3, 2, 1, 4, 5
Г) 3, 1, 2, 4, 5
Д) 3, 4, 2, 1, 5
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 42.25 - 1 = 41.25
|
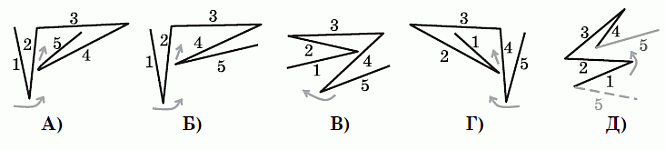
На рисунке показано, как сложить полоску, чтобы числа по слоям располагались так, как указано в ответах А) – Г). (На рисунке показан вид полоски с торца.) Следовательно, правильным может быть только ответ Д, т. е. конфигурация 3, 4, 2, 1, 5 невозможна. Действительно, если сложить полоску так, чтобы началом конфигурации была последовательность 3, 4, 2, 1, то последней после клетки с числом 1 должна быть клетка с числом 5 (пунктирный отрезок на рисунке). Но в действительности на полоске клетка с числом 5 следует после клетки с числом 4 (серый отрезок на рисунке).
Задание 21
|
В ряд расположены двенадцать цветных кубиков: 3 синих, 2 жёлтых, 3 красных и 4 зелёных (но не обязательно в таком порядке). На концах ряда находятся жёлтый и красный кубики. Все красные кубики лежат подряд друг за другом. Все зелёные кубики тоже лежат подряд друг за другом. Десятый слева кубик – синий. Какого цвета шестой слева кубик?
A) зелёного
Б) жёлтого
В) синего
Г) красного
Д) красного или синего
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 41.25 - 1.25 = 40
|
По условию, 10-й слева кубик – синий. На концах ряда расположены жёлтый и красный кубики, причём все 3 красных кубика расположены подряд. Так как после 10-го кубика расположены только два кубика, то тройка красных кубиков не может быть расположена после 10-го кубика и, значит, находится в начале ряда. Следовательно, расположение кубиков имеет вид:
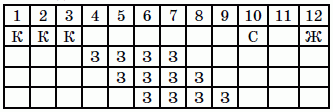
(Здесь К – красный, С – синий, Ж – жёлтый, З – зелёный.)
В последних трёх строчках таблицы приведены все возможные варианты расположения четырёх зелёных кубиков (по условию, они должны быть расположены подряд). Видим, что в любом случае шестой слева кубик является зелёным.
Задание 22
|
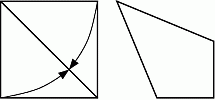
Зина сложила две стороны квадрата по диагонали так, что получился четырёхугольник на рисунке. Чему равна величина максимального угла в полученном четырёхугольнике?
A) 112,5° Б) 120° В) 125° Г) 135° Д) 145°
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 40 - 1.25 = 38.75
|
Пусть Зина сложила квадрат ABCD так, что стороны BA и BC оказались на диагонали BD (см. рис.).
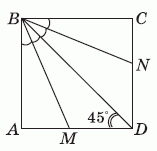
Ясно, что тогда линии сгиба BM и BN делят соответственно углы ∠ABD и ∠CBD, равные 45°, пополам. Поэтому, в частности,
∠MBD = 45° : 2 = 22,5°.
Тогда в треугольнике MBD угол ∠BMD равен
180° – 45° – 22,5° = 112,5°.
Аналогично ∠BND = 112,5°. Таким образом, наибольший угол полученного четырёхугольника равен 112,5°.
Задание 23
|
Сколько существует четырёхзначных чисел A, таких, что половина числа A делится на 2, треть числа А делится на 3, а пятая часть А делится на 5?
A) 1 Б) 7 В) 9 Г) 10 Д) 11
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 38.75 - 1.25 = 37.5
|
Если половина числа A делится на 2, то А делится на 4. Точно так же, если треть числа А делится на 3, то число А делится на 9, и если пятая часть числа А делится на 5, то число А делится на 25. Числа 4, 9, 25 – взаимно простые, т.е. не имеют общих делителей, кроме 1. Поэтому число А делится на 4 · 9 · 25 = 900 и, значит, имеет вид: A = 900n, где n – некоторое
натуральное число. Легко видеть, что такое число будет четырёхзначным только при n = 2, 3, 4, …, 11. Видим, что количество таких чисел равно 10.
Задание 24
|
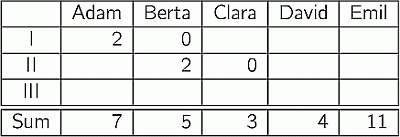
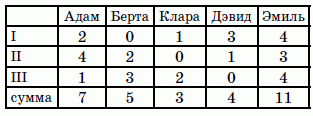
В финале танцевального конкурса каждый из трёх членов жюри присуждает участникам 0, 1, 2, 3 или 4 балла. Ни один судья никаким двум участникам не присуждает одинаковое число баллов. Адам знает суммы баллов всех участников и несколько отдельных оценок, показанных в таблице. Сколько баллов получил Адам от судьи III?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 37.5 + 5 = 42.5
|
Прежде всего, заметим, что в столбце у Берты известны две оценки и суммарная оценка (см. таблицу). Вследствие этого находим, что судья III присудил ей 5 – 0 – 2 = 3 балла. (Будем дописывать в таблицу найденные значения жирными символами.) Далее, Эмиль получил от трёх судей 11 баллов. Эта сумма могла получиться только как 3 + 4 + 4 (в некотором порядке), поскольку 4 – максимальная оценка судей. Судья III оценку 3 уже поставил Берте. Согласно условию, Эмилю он не мог поставить такую же оценку и, значит, поставил 4.
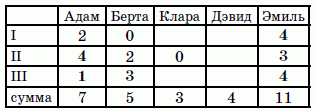
Покажем, что судья I тоже поставил Эмилю 4. Действительно, если бы он поставил Эмилю оценку 3, то оценку 4 он должен был бы поставить Кларе или Дэвиду. Кларе он не мог поставить такую высокую оценку, поскольку у неё сумма баллов 3 – меньше этой оценки. А если бы Дэвид получил оценку 4 от судьи I, то оценки от других судей у него должны были бы равняться 0. Но судья II два поставил оценку 0 Кларе. Противоречие.
Таким образом, Эмиль получил 4 балла от судьи I и судьи III и, значит, 3 балла от судьи II.
Далее, оценку 4 судья II не мог поставить Дэвиду, так как сумма его баллов равна 4 и он не мог получить 0 баллов от судьи I. Следовательно, оценку 4 судья II поставил Адаму. Значит, от судьи III Адам получил 7 – 2 – 4 = 1 балл.
В заключение, хотя для решения задачи этого не нужно, покажем, как выглядит таблица, заполненная целиком.
Задание 25
|
Возле каждой стороны квадрата Светлана записала некоторое натуральное число. Затем возле каждой вершины квадрата она записала произведение чисел возле двух сторон, выходящих из данной вершины. Сумма чисел в вершинах квадрата оказалась равна 15. Чему равна сумма чисел на сторонах квадрата?
A) 6 Б) 7 В) 8 Г) 10 Д) 15
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 42.5 - 1.25 = 41.25
|
Обозначим числа на сторонах квадрата через a, b, c и d (см. рис.).
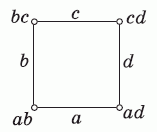
Тогда, по условию,
ab + bc + cd + ad = 15.
Полученное уравнение равносильно
b(a + c) + d(c + a) = 15 ⇔
⇔ (a + c)(b + d) = 15.
Так как, по условию, a, b, c и d – натуральные числа, то
a + c ≥ 2 и b + d ≥ 2.
Поэтому либо a + c = 3, а b + d = 5, либо, наоборот, a + c = 5, а b + d = 3. В любом случае
a + b + c + d = (a + c) + (b + d) = 8.
Хотя правильный ответ уже найден, покажем, что соответствующий набор чисел существует. Действительно, условию задачи удовлетворяют, например,
a = 1, b = 2, c = 2, d = 3.
Задание 26
|
У Софии есть 52 одинаковых равнобедренных прямоугольных треугольника. Она хочет из некоторых из них построить квадраты. Сколько существует квадратов различных размеров, которые она может получить?
A) 6 Б) 7 В) 8 Г) 9 Д) 10
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 41.25 - 1.25 = 40
|
Примем длину катета данных треугольных плиток за 1. Тогда их гипотенузы равны √2. Квадраты можно
получать следующими двумя способами. Можно сложить квадратики из двух данных треугольных плиток, а затем складывать из таких квадратиков бо́льшие квадраты (см. рис.1). Поскольку у Софии имеется 52 треугольные плитки, она может сложить из них 52 : 2 = 26 таких квадратиков. Тогда размеры n х n квадратов, которые из них можно получить, должны быть такими, что n2 ≤ 26, т.е. n ≤ 5. Видим, что таким способом можно сложить 5 различных квадратов.
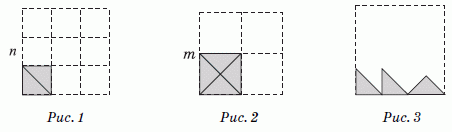
Можно складывать квадраты и по-другому. Сначала сложить квадратики из четырёх треугольных плиток, а затем из
них складывать бо́льшие квадраты (см. рис.2). Число квадратиков такого вида равно 52 : 4 = 13. Тогда размеры m х m квадратов, которые из них можно получить, должны быть такими, что m2 ≤ 13, т.е. m ≤ 3. Поэтому таким способом можно сложить 3 различных квадрата. Поскольку стороны таких квадратов будут состоять из гипотенуз треугольных плиток, их длины будут выражаться нецелыми числами. По этой причине квадраты второго вида не будут совпадать с квадратами первого вида. В результате такими двумя способами София может получить 5 + 3 = 8 различных квадратов.
Теперь покажем, что других квадратов построить нельзя. Действительно, предположим, что сторона квадрата состоит из x катетов и y гипотенуз данных плиток (на рис.3 у нас x = 2, y = 1). Тогда она имеет иррациональную длину x + y√2. Но площадь квадрата выражается рациональным числом, поскольку квадрат составлен из плиток площади 0,5. Однако площадь нашего квадрата равна
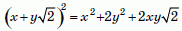 .
.
Это число является рациональным только при условии, что x = 0 или y = 0. Но в таком случае наш квадрат – это какой-то квадрат, полученный одним из двух способов, описанных выше. Таким образом, всего София может сложить из нескольких имеющихся у неё плиток 8 различных квадратов.
Задание 27
|

Коля строит пирамиду из одинаковых шаров. Основание пирамиды квадратное и состоит из 4 × 4 шаров, как показано на рисунке. Следующие слои состоят из 3 × 3 шаров, 2 × 2, а верхний слой состоит из одного шара. В каждой точке соприкосновения двух сфер Коля капнул по капле клея. Сколько всего получилось таких капель?
A) 72 Б) 85 В) 88 Г) 92 Д) 96
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 40 - 1.25 = 38.75
|
Рассмотрим нижний слой пирамиды (см. рис.).
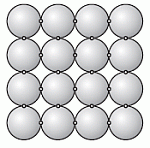
В каждом из четырёх горизонтальных рядов этого слоя имеется по 3 точки касания между шариками данного ряда. Получаем 4 · 3 = 12 точек касания между шариками в горизонтальных рядах. Столько же точек касания имеется и в четырёх вертикальных рядах. Всего между шариками нижнего слоя имеется 12 + 12 = 24 точки касания.
Далее, во втором снизу слое находятся 9 шариков. Каждый из них касается четырёх шариков нижнего слоя. Всего имеем 9 · 4 = 36 таких точек касания. Ещё 36 точек касания имеется между шариками пирамиды, которая получится, если убрать из данной пирамиды нижний слой (см. решение задачи №29, 5-6 классы). Таким образом, всего между шариками пирамиды существует
24 + 36 + 36 = 96 точек соприкосновения и, значит, правильным является ответ Д.
Задание 28
|
Четверо мальчиков находятся в четырёх углах бассейна 10 м × 25 м. Их тренер стоит где-то на одной из сторон бассейна. Когда тренер позвал детей, трое из них вышли из бассейна и пошли к нему по сторонам бассейна по кратчайшему пути. Вместе они прошли 50 метров. Какое наименьшее расстояние до тренера нужно пройти четвёртому мальчику?
A) 10 м Б) 12 м В) 15 м Г) 20 м Д) 25 м
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 38.75 - 1.25 = 37.5
|
Рассмотрим двух мальчиков, которые находятся в диаметрально противоположных углах бассейна (см. рис.).
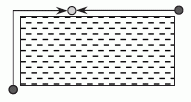
Независимо от того, где стоит тренер, общее расстояние, которое им нужно пройти, равно половине периметра бассейна. Поэтому все четверо мальчиков должны пройти расстояние, равное периметру бассейна, т.е. равное 2 · (10 + 25) = 70 м. Следовательно, если трое из них прошли 50 м, то четвёртый должен пройти 70 – 50 = 20 м.
Задание 29
|
Андрей, Борис и Василий решили устроить гонку. Они стартовали одновременно и бежали с постоянными скоростями. Когда Андрей финишировал, Борису до финиша оставалось
15 метров, а Василию – 35 метров. А когда Борис финишировал, то Василию оставалось до финиша 22 метра. Какова длина дистанции?
A) 135 м Б) 140 м В) 150 м Г) 165 м Д) 175 м
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 37.5 - 1.25 = 36.25
|
Пусть S (м) – расстояние от старта до финиша. Тогда в момент, когда Андрей финишировал, Борис пробежал S – 15 м, а Василий S – 35 м. Поскольку они находились в движении одно и то же время t, то отношение пройденных ими расстояний равно отношению их скоростей:
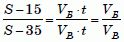 ,
,
где VБ, VВ – скорости Бориса и Василия соответственно.
Далее, когда Борис пробежал расстояние, равное S м, Василий пробежал расстояние S – 22 м. Снова
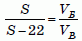 .
.
В результате имеем уравнение:
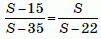
Решая эту пропорцию, получаем:
(S – 15)(S – 22) = S(S – 35), или
S2 – 37S + 330 = S2 – 35S, или
330 = 2S, откуда S = 165.
Задание 30
|
Если сравнить неизвестное четырёхзначное число с некоторыми другими числами, то имеются следующие сведения.
1) 4132 (две цифры правильные, но на неправильных позициях).
2) 9826 (одна цифра правильная и на правильной позиции).
3) 5079 (две цифры верные, но ровно одна из них находится на нужной позиции).
4) 2741 (одна цифра верная, но не на верной позиции).
5) 7642 (ни одна цифра не верна).
Какая цифра является последней у неизвестного числа?
A) 0 Б) 1 В) 3 Г) 5 Д) 9
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 36.25 - 1.25 = 35
|
Согласно последней подсказке, ни одна из цифр 2, 4, 6, 7 не является цифрой неизвестного числа. Поэтому только какие-то четыре из цифр 0, 1, 3, 5, 8, 9 могут быть цифрами этого числа. Тогда из подсказки 1) следует, что цифры 1 и 3 определённо являются цифрами неизвестного числа.
Далее, из подсказки 2) следует, что ровно одна из цифр 8 или 9 является цифрой неизвестного числа (ведь цифры 2, 6 у него отсутствуют).
Проверим, может ли цифра 8 быть цифрой данного числа. В этом случае неизвестное число не имеет цифры 9. Тогда из подсказки 3) следует, что цифры 5, 0 являются цифрами неизвестного числа. Но это невозможно, потому что тогда наше число будет содержать цифры 1, 3, 8, 5, 0, хотя это число четырёхзначное. Противоречие. Значит, цифра 9 находится на первой позиции
искомого числа, а цифра 8 отсутствует.
Ещё раз рассмотрим подсказку 3), согласно которой одна цифра находится в правильной позиции и одна в неправильной. Цифра 9 правильная, но в неправильной позиции (потому что мы
уже знаем, что она находится на первой позиции). Следовательно, цифра 5 не является цифрой неизвестного числа. Иначе мы имели бы по крайней мере две правильные цифры на неправильных местах, что противоречит 3). Следовательно, цифра 0 находится на второй позиции неизвестного числа. В результате число начинается цифрами 90 (в указанном порядке) и заканчивается цифрами 1 и 3 в каком-то порядке.
Из подсказки 1) легко видеть, что последние две цифры должны быть в порядке 13, а не 31. Таким образом, неизвестное число – это число 9013. Его последняя цифра – это цифра 3.
Заметим, что подсказка 4) для нахождения ответа не понадобилась, т.е. она является лишней в условии.





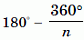 . Из этой формулы видно, что чем больше n, тем больше данный угол.
. Из этой формулы видно, что чем больше n, тем больше данный угол.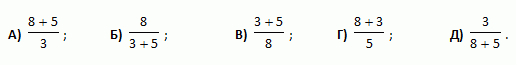
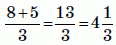
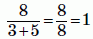
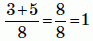
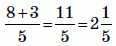
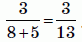
























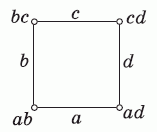

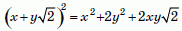 .
.


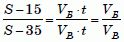 ,
,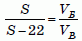 .
.