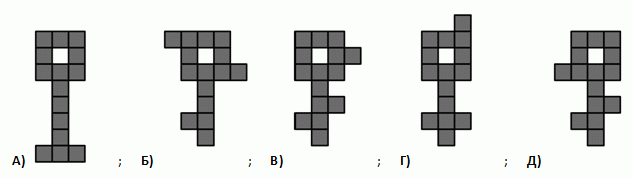Задание 1
|
Гриб растёт непрерывно. Маша фотографировала его каждый день с понедельника по пятницу. Какой из следующих снимков она сделала во вторник?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 24 + 3 = 27
|
Непосредственно в условии задачи видно, что второй по величине гриб изображён на рисунке Д. Поэтому во вторник Маша сделала снимок Д.
Задание 2
|

Какая из следующих плиток дополняет узор на рисунке?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 27 + 3 = 30
|
Дорисуем в центральной клетке
недостающие фрагменты узора.

Сравнивая результат с вариантами ответа, видим, что правильным является ответ Д.
Задание 3
|

Тима решил закрасить все клетки, в которых значение записанного выражения равно 20. Что у него должно получиться?

|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 30 - 0.75 = 29.25
|
Выполним действия, записанные в клетках таблицы. Результаты приведены на рисунке.
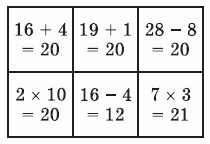
Только во второй и третьей клетках нижней строчки они не равны 20. Значит, только эти две клетки должны остаться неокрашенными. Тем самым, правильным является ответ А.
Задание 4
|
У какой из следующих фигур окрашенная часть имеет наибольшую площадь?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Проще посчитать, у какой из фигур неокрашенная часть наименьшая. В ответе А не окрашены 3 клетки (две целые и 2 половинки, из которых можно составить одну целую клетку). В каждом из следующих ответов не окрашены в общей сложности 3 с половиной клетки. Таким образом, правильным является ответ А.
Задание 5
|
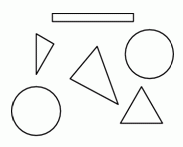
У Коли есть фигурки, изображённые на рисунке. Какую из следующих композиций он может составить из этих фигурок?
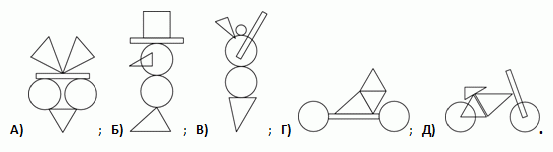
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 32.25 + 3 = 35.25
|
В условии задачи даны 3 треугольника разных размеров, 2 равных круга и 1 вытянутый прямоугольник. В ответах А и Г треугольников три, но среди них в обоих случаях есть два равных. Значит, эти
ответы не являются верными. В ответах Б и В треугольников только два. Значит, и эти ответы не являются верными. Таким образом, верным может быть только ответ Д. И действительно, легко убедиться непосредственно, что «велосипед», изображённый в этом ответе, в точности состоит из набора фигурок из условия задачи.
Задание 6
|
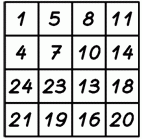
Кенгуру прыгает по клеткам квадрата, начиная с числа 1. Каждый следующий прыжок приходится на клетку с числом, большим на 3. До какого наибольшего числа Кенгуру сможет допрыгать?
A) 11 Б) 14 В) 18 Г) 19 Д) 24
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 35.25 + 3 = 38.25
|

На рисунке показано, что кенгуру может допрыгать до клетки с числом 19. Согласно условию задачи, следующий прыжок должен был бы прийтись на клетку с числом 19 + 3 = 22. Но такого числа в таблице нет. Поэтому кенгуру закончит прыжки на клетке с числом 19.
Задание 7
|

Жора наклеил шесть стикеров на грани кубика. На рисунке показан вид кубика с двух сторон. Какой стикер находится на грани, противоположной грани с уткой?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 38.25 + 3 = 41.25
|
На видимых гранях кубика наклеены пять различных стикеров. Причём на рисунке видно, что у грани с уткой на всех четырёх соседних гранях находятся стикеры с божьей коровкой, мышкой, слоником и собачкой. Поэтому на противоположной грани находится единственный невидимый на этом рисунке стикер – стикер с мухой.
Задание 8
|

Лена хочет разрезать полоску на рисунке по сторонам клеток так, чтобы все части были разной длины. Какое наибольшее число частей у неё может получиться?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Покажем, что полоску нельзя разрезать на шесть или более частей разной длины. Действительно, она состоит из 17 клеток. А сумма шести наименьших натуральных чисел равна
1 + 2 + 3 + 4 + 5 + 6 = 21.
Поэтому нельзя разрезать на шесть или более кусков разной длины. Это можно было бы сделать, только если бы полоска состояла не менее чем из 21 клетки. А пять кусков получить можно, например, если разрезать её так:
1 + 2 + 3 + 4 + 7 = 17
или 1 + 2 + 3 + 5 + 6 = 17.
Задание 9
|
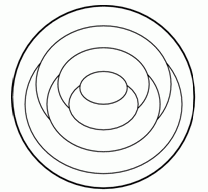
Света окрашивает каждую часть круга на рисунке в красный, синий или жёлтый цвет. Части, имеющие общую границу, она красит в разные цвета. Внешнюю часть Света окрасила в красный цвет. Сколько всего частей она окрасит в красный цвет?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 40.5 - 1 = 39.5
|
Начнём с красной внешней части и продолжим окраску, продвигаясь к центру. В результате может получиться только два способа полной окраски, которая удовлетворяет условию задачи. Один из них показан на рисунке ниже.

Другой можно получить, если перекрасить синие части в жёлтый цвет, а жёлтые – в синий. В любом случае получаем 3 красные части.
Задание 10
|
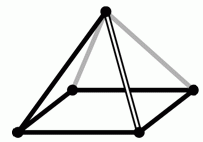
Леся смотрит на пирамиду сверху. Что она видит?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 39.5 + 4 = 43.5
|
На рисунке в условии задачи видим, что
пирамида имеет два серых боковых ребра. Если просматривать их сверху по ходу часовой стрелки, то они расположены друг за другом, и после второго серого ребра идёт белое ребро (см. рис.).
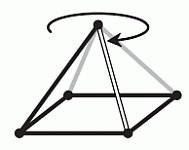
Поэтому ответы А и Д не являются верными: на них только одно серое боковое ребро. В ответе Б серые рёбра расположены не друг за другом, а напротив друг друга. Поэтому и ответ Б также неверный. Если просматривать боковые рёбра по ходу часовой стрелки в ответе Г, то за двумя последовательно расположенными серыми рёбрами идёт не белое, а чёрное ребро. Следовательно, и этот ответ неверный. А в ответе B боковые рёбра действительно расположены так, как на рисунке данной пирамиды в условии задачи. Поэтому правильным является ответ В.
Задание 11
|
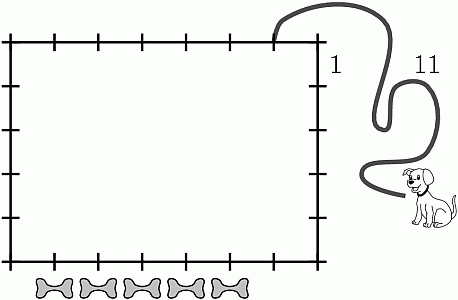
Денис привязал собаку на поводок длиной 11 метров на расстоянии 1 метр от угла сарая 7 × 5 метров. Возле сарая лежат 5 косточек, как показано на рисунке. До скольких из них собака может добраться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 43.5 + 4 = 47.5
|
Запишем в обе стороны расстояния (в метрах) от точки, где привязана собака, до отмеченных точек на стенах сарая (см. рис.).
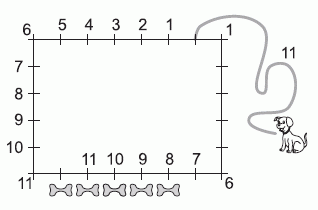
Видим, что если пёс будет двигаться вдоль стен сарая против хода часовой стрелки, то он не доберётся ни до одной косточки. А если пёс будет двигаться по ходу часовой стрелки, то он может добраться до 4 косточек.
Задание 12
|
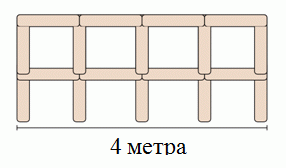
Лёня строит забор из столбов длины 1 метр. На рисунке показан его фрагмент забора длиной 4 метра. Сколько всего столбов нужно Лёне, чтобы построить 10-метровый забор?
A) 22 Б) 30 В) 33 Г) 40 Д) 42
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 47.5 - 1 = 46.5
|
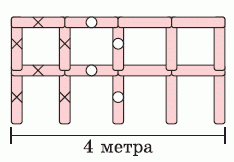
На рисунке видно, что для построения первого (левого) метра забора понадобилось 6 столбов (на рисунке они помечены крестиком). Для того чтобы достраивать забор справа, на каждый метр нужно 4 столба (на рисунке они помечены кружочками). Поэтому для дополнительных 9 метров понадобится 9 · 4 = 36 столбов. Таким образом, 10-метровый забор будет состоять из 6 + 36 = 42 столбов.
Задание 13
|
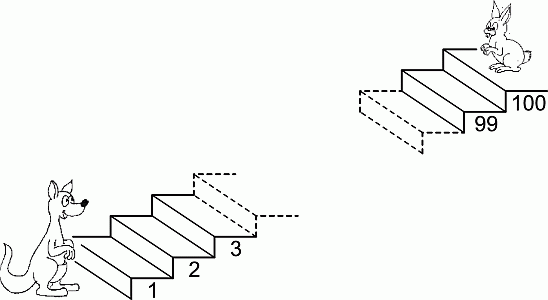
Каждый раз, когда Кенгуру прыгает на 7 ступенек вверх, Кролик прыгает на 3 ступеньки вниз. На какой ступеньке они встретятся?
A) 53 Б) 60 В) 63 Г) 70 Д) 73
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 46.5 + 4 = 50.5
|
Кенгуру и Кролика разделяют 100 ступенек. За каждую пару прыжков (прыжок Кенгуру и прыжок Кролика) они приближаются друг к другу на 7 + 3 = 10 ступенек. Поэтому они встретятся через 100 : 10 = 10 пар таких прыжков. После 10 прыжков Кенгуру окажется на 10 · 7 = 70 ступеньке. Следовательно, на 70-й ступеньке они и встретятся.
Задание 14
|
Карина задумала три числа. Их сумма равна 50. Из каждого задуманного числа Карина вычла некоторое секретное число. В результате она получила 24, 13 и 7. Какое из следующих чисел является одним из задуманных чисел?
A) 9 Б) 11 В) 13 Г) 17 Д) 23
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 50.5 + 4 = 54.5
|
Сумма полученных Кариной чисел равна 24 + 13 + 7 = 44. Видим, что после того, как Карина из каждого задуманного числа вычла секретное число, сумма задуманных чисел уменьшилась на 50 – 44 = 6. Значит, из трёх задуманных чисел она вычитала число 6 : 3 = 2. Следовательно, задуманными числами были числа 24 + 2 = 26, 13 + 2 = 15 и 7 + 2 = 9. Из них только число 9 встречается в вариантах ответа. Поэтому правильным является ответ А 9.
Задание 15
|
Амалия хочет построить корону из 10 одинаковых пятиугольников вида
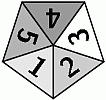 .
.
Они должны соприкасаться сторонами треугольников с одинаковыми числами. Какое число окажется в треугольнике, отмеченном знаком X?
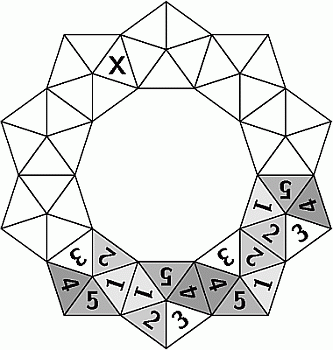
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 54.5 - 1 = 53.5
|
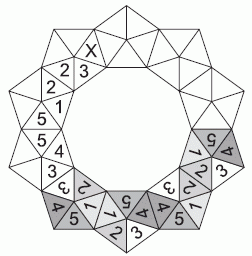
Числа в пятиугольниках расположены по кругу в порядке 1-2-3-4-5, если их просматривать против хода часовой стрелки. Поэтому, следуя данному порядку, можно вписать числа в незаполненные треугольники так, как показано на рисунке. Треугольник, отмеченный крестиком, идёт следующим после числа 3. Следовательно, в этом треугольнике должно быть число 4.
Задание 16
|
У Феди есть два вида палочек: короткие длиной 1 см и длинные длиной 3 см. Из какого из следующих наборов палочек Федя может сложить квадрат, если палочки нельзя ломать и накладывать друг на друга?
A) 5 коротких, 2 длинных
Б) 3 коротких, 3 длинных
В) 4 коротких, 2 длинных
Г) 6 коротких
Д) 6 длинных
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 53.5 - 1 = 52.5
|
Если квадрат построен из спичек с целыми длинами, то длины его сторон также выражаются целыми числами. Так как у квадрата четыре равные стороны, то его периметр (сумма длин сторон) делится на 4. Подсчитаем суммы длин спичек в вариантах ответа. Имеем:
А) 5 · 1 + 2 · 3 = 11,
Б) 3 · 1 + 3 · 3 = 12,
В) 4 · 1 + 2 · 3 = 10,
Г) 6 · 1 = 6,
Д) 6 · 3 = 18.
Видим, что только в ответе Б сумма длин спичек делится на 4. Поэтому все другие ответы не являются верными. А квадрат из набора спичек в варианте Б Федя действительно может
сложить (три стороны по одной длинной спичке, одна сторона из трёх коротких).
Задание 17
|
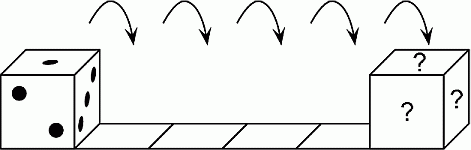
У стандартного кубика сумма точек на противоположных гранях равна 7. Кубик лежит так, как показано на рисунке. Чему будет равна сумма точек на гранях, отмеченных знаком «?» после пяти перекатываний вправо?
A) 6 Б) 7 В) 9 Г) 11 Д) 12
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 52.5 - 1.25 = 51.25
|
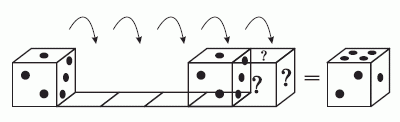
По условию задачи, кубик перекатили через рёбра вправо 5 раз. Ясно, что ровно через 4 перекатывания его грани будут расположены, как вначале (см. рис.). Ещё через одно перекатывание получим окончательный результат, при котором грань с тремя точками окажется внизу. Так как сумма точек на противоположных гранях равна 7, то на верхней окажется 7 – 3 = 4 точки. Следовательно, сумма точек на гранях, отмеченных знаком «?» после пяти перекатываний, будет равна 4 + 2 + 1 = 7.
Задание 18
|
Шестеро школьников заказали по одному шарику мороженого: 3 ванильного, 2 шоколадного и 1 лимонного. Они добавили к мороженым 3 вишни, 2 вафли и 1 дольку мандарина, к каждому мороженому что-то одно. При этом одинаковых сочетаний не получилось. Какое из следующих сочетаний не могло получиться?
A) шоколадное с вишней
Б) ванильное с вишней
В) лимонное с вафлей
Г) шоколадное с вафлей
Д) ванильное с мандарином
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 51.25 - 1.25 = 50
|
По условию, школьники заказали 3 ванильных мороженых и добавки к ним были разного вида из трёх возможных. Значит, было ванильное мороженое с вишней, ванильное мороженое с вафлей и ванильное мороженое с мандаринкой. Уже видим, что ответы Б и Д не являются верными.
Далее, на остальные мороженые (2 шоколадных и 1 лимонное) остаются в качестве добавок 2 вишни и 1 вафля. Так как, по условию, и шоколадные мороженые были с разными добавками, то одно шоколадное мороженое было с вишней, а другое – с вафлей. Стало быть, ответы А и Г также не являются верными. Кроме того, получаем, что лимонное мороженое было с вишней, а не с вафлей, как в ответе В. Поэтому верный ответ – это ответ В.
Задание 19
|
У людей некоторых народов бывает несколько имен. Один из братьев Гримм решил узнать, как зовут невесту его брата. Он задал ей 3 вопроса: "Вас зовут Адель Лилли Клео?", "Вас зовут Адель Лаура Кора?", "Вас зовут Эбби Лора Клео?" Каждый раз ровно одно имя было верным и стояло на нужном месте. Как зовут невесту брата?
A) Эбби Лили Кора
Б) Эбби Лаура Кора
В) Адель Лаура Клео
Г) Адель Лили Кора
Д) Эбби Лаура Клео
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Выпишем в виде таблицы тройки имён, которые были названы в заданных вопросах.
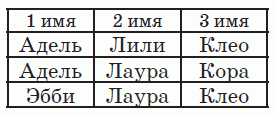
Видим, что в первом столбце дважды присутствует имя Адель. Предположим, что оно верное. Тогда имя Эбби на первом месте – неправильное имя. Рассмотрим имена во втором столбце. Ни Лили, ни Лаура не являются верными именами (иначе в первой и во второй строчках было бы более одного верного имени). По такой же причине, рассматривая третий столбец, заключаем, что ни Клео, ни Кора не являются верными именами. Но тогда ни во второй, ни в третьей строчках нет ни одного верного имени – противоречие. Следовательно, имя Адель – неверное имя.
Теперь рассмотрим второй столбец (второе имя). В нём дважды встречается имя Лаура. Если предположить, что оно верное, то в первом столбце Адель и Эбби не являются верными, а в третьем столбце Кора и Клео не являются верными. Кроме того, Лили и Лаура не могут быть одновременно верными. В результате, в первой строчке имён нет ни одного верного, что противоречит условию. Значит, Лаура – неверное имя.
Наконец, рассмотрим имя Клео в третьем столбце. Предположив, что оно – правильное третье имя, как и раньше, приходим к аналогичному противоречию. Значит, Клео – неправильное имя.
Вычеркнем в каждом столбце найденные неправильные имена. Получим единственную возможную тройку правильных имён Эбби Лили Кора.
По-другому правильный ответ можно было получить, просто просмотрев по очереди все предложенные варианты ответа. Проверяя каждый из них на выполнение всех условий задачи, сразу можно обнаружить, что вариант А им удовлетворяет. Следовательно, согласно условиям конкурса, именно он – тот единственный, который является правильным.
Задание 20
|
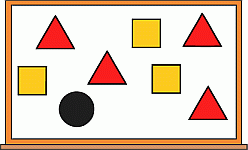
Учитель написал все числа от 1 до 8 на доске. Затем он закрыл их треугольниками, квадратами и кружочком. Сумма всех чисел, закрытых треугольниками, равна 10, а сумма всех чисел, закрытых квадратами, равна 20. Какое число закрыто кружком?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 48.75 + 5 = 53.75
|
Сумма всех восьми данных чисел равна
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
Согласно условию, сумма чисел, закрытых треугольниками и квадратами, равна
10 + 20 = 30.
Поэтому кружочком закрыто число
36 – 30 = 6.
Пример распределения чисел по треугольникам и квадратам для решения задачи не обязателен. Но его легко построить:
1 + 2 + 3 + 4 = 10,
5 + 7 + 8 = 20.
Задание 21
|

У Жени есть несколько одинаковых рисунков попугаев. Она хочет раскрасить голову, хвост и крылья каждого попугая в красный, синий и зелёный цвета так, чтобы все три цвета присутствовали на каждом рисунке. Она окрасила голову одного попугая в красный цвет, крылья – в зелёный, а хвост – в синий. Сколько ещё попугаев она может раскрасить так, чтобы все попугаи были окрашены по-разному?
A) 1 Б) 2 В) 4 Г) 5 Д) 8
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 53.75 - 1.25 = 52.5
|
Все способы раскраски, о которых говорится в условии, можно выписать непосредственно. Они приведены в таблице.
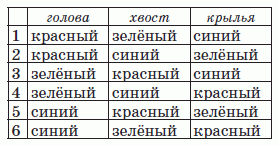
Видим, что, помимо первого способа, указанного в условии задачи, существует ещё 5 таких способов.
Задание 22
|
В летний лагерь «Кенгуру» съехались 43 школьника из нескольких стран, по 5 или 6 человек из каждой страны. Сколько стран прислали школьников в этот лагерь?
A) 4 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 52.5 + 5 = 57.5
|
Так как 43 < 5 · 9 = 45, то число стран, приславших своих школьников в летний лагерь «Кенгуру», меньше 9.
Далее, так как 43 > 6 · 7 = 42, то число стран, приславших своих школьников в лагерь, больше 7. Значит, только 8 стран могли прислать своих школьников в данный лагерь.
Пример распределения количества школьников по странам не обязателен, так как правильный ответ уже найден. Но этот пример легко построить. Если 5 стран пришлют по 5 школьников и 3 страны – по 6 школьников, то всего 5 + 3 = 8 стран пришлют в точности
5 · 5 + 3 · 6 = 25 + 18 = 43 школьника.
Задание 23
|
Какую из следующих фигур нельзя разрезать на три различные связные части с одинаковым количеством клеток? Разрезы можно делать только по сторонам клеток.
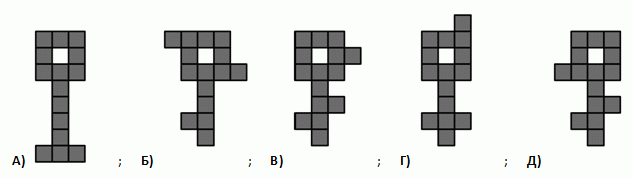
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 57.5 - 1.25 = 56.25
|
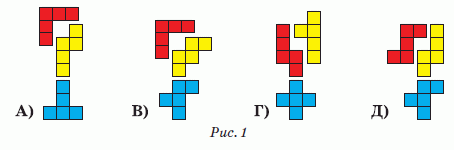
Прежде всего заметим, что все данные фигуры состоят из 15 клеток. Поэтому части, на которые их нужно разрезать, должны состоять из 5 клеток. На рис.1 показано, как разрезать фигуры А, В, Г и Д соответственно, на связные пятиклеточные части, среди которых нет равных. Значит, верным может быть только ответ Б.
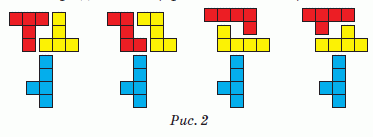
Действительно, все возможные способы разрезания фигуры Б на три связные пятиклеточные части показаны на рис.2. При всех способах по крайней мере две части (красная и жёлтая) являются равными.
Задание 24
|
Какое наибольшее значение может иметь выражение
KAN + GA – ROO,
если в нём буквы заменить ненулевыми цифрами (одинаковые буквы – одинаковыми цифрами, а разные – разными).
A) 925 Б) 933 В) 939 Г) 942 Д) 948
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 56.25 - 1.25 = 55
|
Чтобы выражение KAN + GA – ROO имело наибольшее значение, необходимо, чтобы ROO было наименьшим, а KAN + GA – наибольшим. Учитывая, что все буквы обозначают ненулевые цифры, наименьшее значение ROO равно 122. Наибольшее значение у числа будет, если выполняется условие: чем старше цифра, тем она больше. Поэтому цифрой сотен, которая соответствует букве K, должна быть цифра 9, а цифрами десятков A и G должны быть цифры 8 и 7 в каком-то порядке. В первом случае наибольшее значение
KAN + GA = 98N + 78 = 986 + 78 = 1064.
Во втором случае наибольшее значение
KAN + GA = 97N + 87 = 976 + 87 = 1063.
Следовательно, наибольшее значение
KAN + GA – ROO = 986 + 78 – 122 = 1064 – 122 = 942.
По-другому правильный ответ можно было получить так. Перепишем данное выражение в виде
KAN + GA – ROO = (100 · K + 10 · A + N) + (10 · G + A) – (100 · R + 10 · O + O) = 100 · (K – R) + 11 · A +10 · G + N – 11 · O.
Тогда видно, что данное выражение принимает наибольшее значение, если
(K – R) = (9 – 1) = 8,
A = 8, G = 7, N = 6 и O = 2.
Подставив в данное выражение вместо букв найденные значения, получим такой же результат: 942.









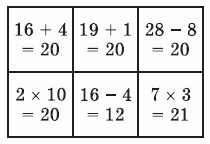


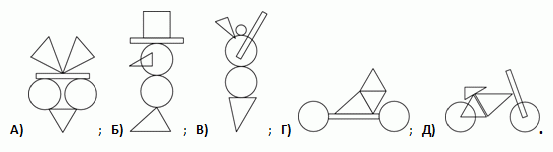















 .
.