Задание 1
|
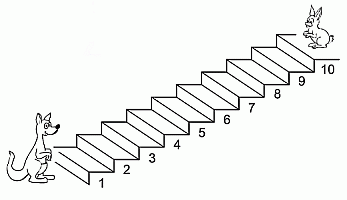
Каждый раз, когда Кенгуру прыгает на 3 ступеньки вверх, Кролик прыгает на 2 ступеньки вниз. На какой ступеньке они встретятся?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 24 - 0.75 = 23.25
|
После первого прыжка Кенгуру окажется на 3-й ступеньке, а Кролик – на 10 – 2 = 8-й ступеньке. Ещё после одного прыжка Кенгуру окажется на 3 + 3 = 6-й ступеньке и Кролик тоже на 8 – 2 = 6-й ступеньке. Видим, что они встретятся на 6-й ступеньке.
Задание 2
|

Маша делает селфи на фоне замка, изображённого на рисунке. Какой снимок у неё может получиться?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 23.25 + 3 = 26.25
|
Замок имеет 3 треугольные башни. Средняя из них выше крайних. Между первой и второй треугольными башнями находится 1 прямоугольная башня, а между второй и третьей – 2 прямоугольные башни. Всего имеется 3 прямоугольные башни. Поэтому У Миши не могли получиться снимки А и Б: на них 4 прямоугольные башни. Не мог получиться снимок В: на нём нет самой высокой треугольной башни. Не мог получиться и снимок Г: на нём первая и вторая треугольные башни имеют одинаковую высоту. А снимок в ответе Д полностью соответствует рисунку замка в условии задачи. Следовательно, правильным является ответ Д.
Задание 3
|
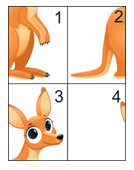
В каком порядке нужно сложить 4 карточки на рисунке, чтобы получился рисунок кенгуру?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 26.25 + 3 = 29.25
|
Рассмотрев карточки в условии задачи, можно заключить, что карточка 2 должна быть левее карточки 1, а карточка 3 – выше карточки 1. Эти условия выполняются только в ответе А.
Задание 4
|
Федя выкладывает игрушки из коробки в порядке, повторяющемся через каждые 5 игрушек. Какими будут следующие две игрушки?


|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Последней в ряду из условия задачи находится мышка. Кроме того, в этом ряду видим, что после мышки идут улитка и птичка. Поэтому правильным является ответ Д.
Задание 5
|
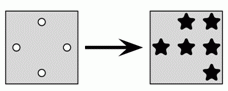
У Васи есть две карточки одинакового размера. На первой карточке имеются 4 отверстия, а на второй нарисованы 6 звёздочек. Вася наложил первую карточку на вторую. Что он может увидеть?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 32.25 + 3 = 35.25
|
На первой карточке имеется 4 отверстия, и они находятся возле середин сторон данной карточки (см. рис. в условии задачи). На второй карточке имеются звёздочки возле середин всех сторон, кроме нижней стороны. Поэтому после наложения карточек только нижнее отверстие не будет выглядеть чёрным, как в ответе А.
Задание 6
|
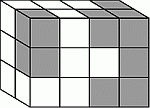
Маша собрала блок из 14 серых и нескольких белых кубиков. Сколько серых кубиков не видно на этом рисунке?
A) 1 Б) 3 В) 5 Г) 6 Д) 8
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Блок на рисунке в условии задачи состоит из трёх горизонтальных слоёв, по 8 кубиков в каждом. В верхнем слое видно 4 серых кубика, в среднем и нижнем слое – по 2 серых кубика. Таким образом, на рисунке видно 4 + 2 + 2 = 8 серых кубиков. А всего, по условию, в блоке 14 серых кубиков. Поэтому на рисунке блока не видно 14 – 8 = 6 серых кубиков.
Задание 7
|
Аня нарисовала на листе бумаги несколько треугольников и квадратов. Среди них ровно три чёрных треугольника и менее четырёх квадратов. Как может выглядеть рисунок Ани?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 34.5 + 3 = 37.5
|
На рисунке A) имеется два чёрных треугольника, а на рисунках B) и Г) – только по одному. Поэтому соответствующие ответы не являются верными. На рисунке Б) – ровно три чёрных треугольника, но на этом рисунке четыре квадрата, что также не соответствует условию задачи. Поэтому правильным является ответ Д). Действительно, на соответствующем рисунке три чёрных треугольника и три (т.е. менее
четырёх) квадрата.
Задание 8
|
Настя сплела косичку из трёх верёвок: зелёной (з), синей (с) и красной (к). Какого цвета верёвки 1, 2 и 3?

A) 1 – синяя, 2 – зелёная, 3 – красная
Б) 1 – красная, 2 – синяя, 3 – зелёная
В) 1 – зелёная, 2 – красная, 3 – синяя
Г) 1 – синяя, 2 – красная, 3 – зелёная
Д) 1 – зелёная, 2 – синяя, 3 – красная
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 37.5 + 3 = 40.5
|
Прорисуем с левого конца до правого сначала зелёную ленточку, а затем синюю (см. рис.).
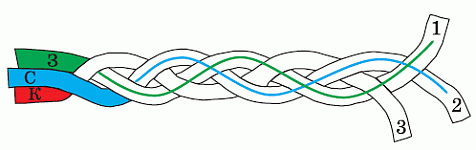
Видим, что ленточка 1 – зелёная, ленточка 2 – синяя и, значит, ленточка 3 – красная.
Задание 9
|

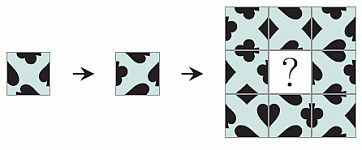
Какой квадратик нужно поместить в центр данного рисунка, чтобы дополнить узор?

|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 40.5 - 1 = 39.5
|
По краям квадратика, отсутствующего в центре узора, находятся половинки следующих карточных мастей: слева – ♣ (трефы), сверху и справа – ♠ (пики), а снизу – ♥ (черви). Просматривая варианты ответа, видим, что такой набор половинок этих мастей
имеет только плитка В). Поэтому только ответ В может быть верным. И действительно, если повернуть эту плитку на четверть оборота против хода часовой стрелки и поместить в центр рисунка, то узор восстановится (см. рис.).
Задание 10
|
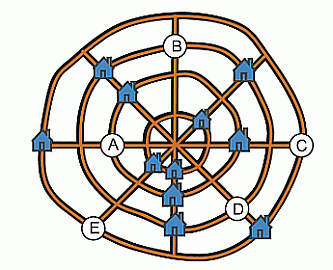
В деревне есть 12 домов, 4 прямые и 4 кольцевые дороги. На каждой прямой дороге и на каждой кольцевой дороге расположены по 3 дома. На рисунке показано 11 домов. На каком перекрёстке должен быть 12-й дом?
A) А Б) В В) С Г) D Д) E
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 39.5 + 4 = 43.5
|
На рисунке в условии видно, что на внешней кольцевой дороге и на горизонтальной дороге расположены только по два дома. Следовательно, 12-й дом должен быть расположен на пересечении этих дорог, т. е. на перекрёстке C.
Задание 11
|
Вася построил 5 фигур, склеив кубики по граням. Для какой фигуры понадобилось больше всего кубиков?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 43.5 + 4 = 47.5
|
Подсчитаем для каждой фигуры количество кубиков, из которых она склеена. Получим следующие результаты.

Видим, что в любом случае больше всего кубиков понадобилось для построения фигурки Д).
Задание 12
|
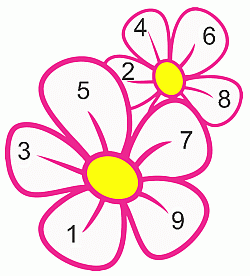
На лепестках двух цветков записаны числа так, что суммы чисел на этих цветках одинаковы. Какое число записано на скрытом лепестке меньшего цветка?
A) 1 Б) 3 В) 5 Г) 7 Д) 2
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 47.5 + 4 = 51.5
|
Сумма чисел на лепестках большего цветка равна 1 + 3 + 5 + 7 + 9 = 25. Сумма чисел на видимых лепестках меньшего цветка равна 2 + 4 + 6 + 8 = 20. Следовательно, согласно условию, число на скрытом лепестке равно 25 – 20 = 5.
Задание 13
|
На каком из следующих рисунков серая часть имеет наибольшую площадь?

|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 51.5 - 1 = 50.5
|
На рисунках в условии задачи все квадраты равны друг другу. Поэтому серая часть наибольшая у того квадрата, который имеет наименьшую белую часть. У квадрата Б) 3 половинки клеток белые. У остальных квадратов – по 4 такие половинки (некоторые из них образуют целые белые клетки). Таким образом, правильным является ответ Б.
Задание 14
|

Маша хочет вписать числа 1, 2, 3, 4, 5 и 6 в клетки на рисунке (каждое ровно в одну из клеток) так, чтобы сумма чисел в трёх синих клетках и сумма чисел в двух жёлтых клетках равнялись 10. Какое число она должна вписать в клетку со знаком вопроса?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 50.5 - 1 = 49.5
|
Сумма всех чисел, которые хочет вписать Маша, равна
1 + 2 + 3 + 4 + 5 + 6 = 21.
Согласно условию, сумма чисел в трёх синих и двух жёлтых клетках должна быть равна 10 + 10 = 20. Поэтому в клетку со знаком вопроса должно быть вписано число 21 – 20 = 1.
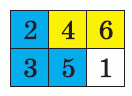
Хотя правильный ответ уже найден, покажем, что числа вписать в таблицу так, как требуется, можно (см. рис.);
этот пример далеко не единственный.
Задание 15
|
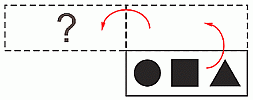
На столе лежала карточка с тремя нарисованными на ней фигурами. Миша перевернул карточку сначала вверх, потом налево (см. рис.). Что он видит на карточке?

|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 49.5 - 1 = 48.5
|
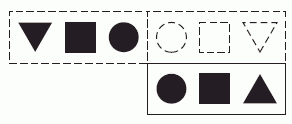
На рисунке показаны результаты обоих переворачиваний. Сравнивая окончательный результат с вариантами ответа, видим, что правильным является ответ Б.
Задание 16
|
Бабушка печёт пирожки для своих пяти внучат. Она уже испекла 12 пирожков. Какое наименьшее число пирожков ей ещё нужно испечь, чтобы всем внучатам досталось поровну пирожков?
A) ни одного Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 48.5 - 1 = 47.5
|
Чтобы каждому из пяти внуков досталось пирожков поровну, нужно, чтобы их число делилось на 5. Наименьшее число, которое делится на 5 и больше 12, – это число 15. Поэтому бабушке нужно испечь ещё 3 пирожка.
Задание 17
|
У Толи есть 9 плиток с фигурками трёх видов (кружочками, треугольничками и квадратиками):

Он хочет разместить эти плитки в клетках квадрата так, чтобы в каждой строчке и каждом столбце были фигурки каждого вида, и не было плиток с одинаковым количеством фигурок. Три плитки он уже положил так, как показано на рисунке.

Какой должна быть плитка в серой клетке?

|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 47.5 - 1.25 = 46.25
|
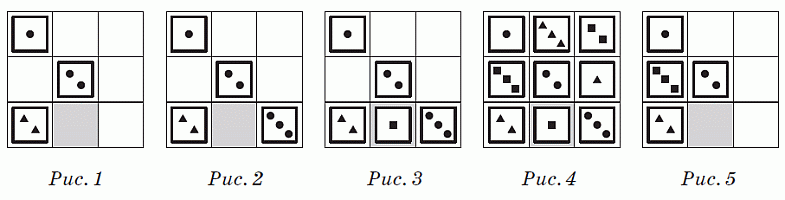
В первых двух строчках уже есть плитки с кружочками (см. рис.1). Поэтому ещё одна плитка с (тремя) кружочками должна быть в третьей строчке. Точно так же, поскольку в первых двух столбцах есть плитки с кружочками, то третья плитка с
кружочками должна быть в третьем столбце. Итак, плитка с тремя
кружочками должна находиться в правой нижней клетке таблицы (см. рис.2).
Далее, в нижней строчке уже есть плитка с двумя фигурками и плитка с тремя фигурками. Поэтому в серой клетке должна быть плитка с одной фигуркой. Кроме того, фигурки на этих двух плитках – это фигурки с треугольничками и кружочками. Поэтому в серой клетке должна быть фигурка с одним квадратиком (см. рис.3). Таким образом, правильным является ответ Г.
Хотя правильный ответ уже найден, покажем, что можно продолжить заполнение таблицы так, что все условия задачи будут выполнены (см. рис.4).
По-другому правильный ответ можно было найти, например, так. В левом столбце уже есть плитка с кружочком и плитка с трегольничками (см. рис.1). Следовательно, не хватает плитки с квадратиками. И на этой плитке должно быть три квадратика, потому что на имеющихся плитках находятся одна фигурка и две фигурки (см. рис.5).
Далее, в строчке и столбце, на пересечении которых находится серая клетка, имеются плитки с кружочками и треугольниками. Значит, в этой клетке должна быть плитка с квадратиками. И на этой плитке не может быть две фигурки. Плитка с тремя квадратиками уже использована. Значит, в серой клетке должна быть плитка с одним квадратиком.
Задание 18
|
Два одинаковых поезда, состоящие из 31-го вагона, движутся навстречу друг другу по соседним путям. Какой вагон будет напротив 12-го вагона первого поезда, когда 19-е вагоны окажутся напротив друг друга?
A) 7 Б) 12 В) 21 Г) 26 Д) 31
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 46.25 - 1.25 = 45
|
12-й вагон первого поезда находится на 19 – 12 = 7 вагонов впереди 19-го вагона. Поэтому когда 19-й вагон этого поезда поравняется с 19-ым вагоном встречного поезда, то у встречного поезда напротив 12-й вагона будет вагон, который находится на 7 вагонов позади 19-го вагона, т. е. вагон номер 19 + 7 = 26.
По-другому ответ можно было получить непосредственно из соответствующего задаче рисунка:

Задание 19
|
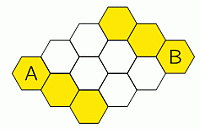
Пчёлка Майя может ползать только по жёлтым ячейкам сот. Она хочет переползти из ячейки А в ячейку B. Для этого разрешается перекрасить в жёлтый цвет ровно две белые ячейки. Сколько существует способов это сделать?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 45 - 1.25 = 43.75
|
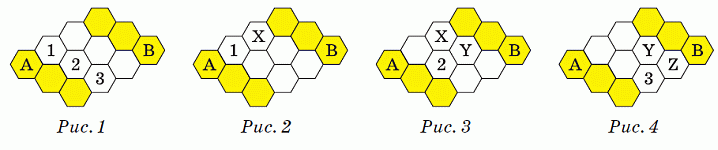
Чтобы перебраться от тройки серых сот с сотой А к тройке серых сот с сотой В, необходимо пройти через какую-то из сот 1, 2 или 3 на рис.1. Следовательно, по крайней мере одна из
них должна быть окрашена в жёлтый цвет. Если жёлтой будет сота 1, то второй жёлтой сотой может быть только сота X (см. рис.2). Если жёлтой будет сота 2, то второй жёлтой сотой может быть только сота X или Y (см. рис.3). А если жёлтой будет сота 3, то второй жёлтой сотой может быть только сота Y или Z (см. рис.4). Таким образом, существует 1 + 2 + 2 = 5 способов окрасить две белые соты в жёлтый цвет так, чтобы по жёлтым сотам можно было добраться от соты А до соты В.
Задание 20
|
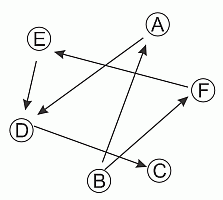
На рисунке кружочками изображены 6 человек. Стрелка, соединяющая два кружочка, указывают на того, кто из них выше. Кто самый высокий?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 43.75 + 5 = 48.75
|
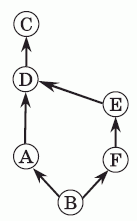
Перерисуем схему из условия задачи так, чтобы не было пересечения стрелок и чтобы тот, кто выше, располагался на рисунке выше, т. е. чтобы стрелки шли снизу вверх. Согласно схеме в условии задачи, в кружочек B не входит ни одна стрелка. Поэтому расположим его внизу рисунка. Выше В, согласно
схеме из условия, расположим кружочки А и F и т. д. (см.
рис.). Видим, что самым высоким является С.
Задание 21
|
В корзине 8 груш и несколько яблок, все зелёные или жёлтые. Количество жёлтых груш равно 6. Яблок в корзине на 3 больше, чем всех зелёных фруктов. Сколько жёлтых яблок в корзине?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
Составим таблицу, в которую внесём данные из условия задачи. Пусть строчкам соответствуют фрукты, столбцам – их цвет. Число зелёных яблок мы не знаем,
обозначим ЗЯ (таблица 1). Видим, что зелёных груш 8 – 6 = 2 (см. таблицу 2). А тогда всего зелёных фруктов ЗЯ + 2. По условию, всего яблок на 3 больше, чем всех зелёных фруктов. Поэтому всего зелёных яблок ЗЯ + 5 (таблица 2). По первой строчке таблицы 2 видим, что жёлтых яблок должно быть 5.

Задание 22
|
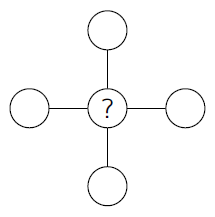
Рома вписывает числа 1, 2, 3, 4 и 5 в кружочки на рисунке так, чтобы сумма трёх чисел на вертикали равнялась сумме трёх чисел на горизонтали. Какое число может быть вписано в центральном кружочке?
A) только 5
Б) 2, 3 и 4
В) только 3
Г) только 1 и 3
Д) 1, 3 и 5
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 47.5 - 1.25 = 46.25
|
Среди данных пяти чисел есть два чётных числа (делятся на 2) и три нечётных (не делятся на 2). Сложим все данные пять чисел, получим
1 + 2 + 3 + 4 + 5 = 15.
Если к этой сумме ещё один раз прибавить число в центре, то мы должны получить чётное число. Действительно, это будет сумма двух равных сумм: суммы трёх чисел на вертикали и суммы трёх чисел на горизонтали. Следовательно, так как 15 – нечётное число, то добавляемое число, т. е. число в центре схемы, также должно быть нечётным. Следующие примеры удовлетворяют условию задач и показывают, что это может быть любое из чисел 1, 3, 5.
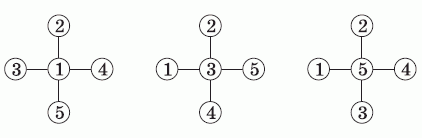
Задание 23
|

На гранях куба записаны 6 различных натуральных чисел, не меньших 1 и не больших 9. Суммы чисел на противоположных гранях – одинаковые. Какое число записано на грани, противоположной грани с числом 5?
A) 3 Б) 5 В) 6 Г) 7 Д) 9
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 46.25 + 5 = 51.25
|
По условию, суммы чисел на противоположных гранях равны. На рисунке видно, что на одной из граней куба есть число 8. А наименьшее число на противоположной грани, по условию, не меньше 1. Поэтому сумма чисел на каждой из противоположных граней не меньше, чем 1 + 8 = 9.
Далее, наименьшее число на гранях куба, которое мы видим, – число 4. А напротив, на невидимой грани, расположено, согласно условию, число, не большее 9. Поэтому наибольшее значение суммы чисел на противоположных гранях не больше 4 + 9 = 13. Следовательно, суммы чисел на противоположных гранях не могут быть другими, кроме 9, 10, 11, 12 и 13. А тогда напротив грани с числом 5 не может
быть другого числа, кроме 9 – 5 = 4, 10 – 5 = 5, 11 – 5 = 6, 12 – 5 = 7 и 13 – 5 = 8. Но, по условию, все числа на гранях различны, а числа
4, 5, 8 уже есть на видимых гранях. Следовательно, на грани против числа 5 может быть только число 6 или число 7. Но число 7 не подходит. Иначе, сумма чисел на противоположных гранях должна быть
равна 7 + 5 = 12. А тогда против числа 4 должно быть число 12 – 4 = 8,
которое уже есть на видимой грани кубика в условии задачи. Таким образом, единственным правильным ответом
может быть только 6.
Подтверждающий пример для этого не
обязателен. Но он, действительно, существует (см. рис.).
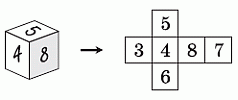
Задание 24
|
Женя и Оля обменивались конфетами. Сначала Женя дал Оле столько конфет, сколько было у Оли. Затем Оля дала Жене столько конфет, сколько осталось у Жени после первого обмена. В результате у обоих осталось по 4 конфеты. Сколько конфет было у Жени вначале?
A) 6 Б) 5 В) 4 Г) 3 Д) 2
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 51.25 - 1.25 = 50
|
Согласно условию, у детей вместе было 8 конфет, так как в конце их стало по 4. На втором шаге Оля дала Жене столько конфет, сколько у Жени было до этого. Это значит, что число конфет у Жени удвоилось. И так как их стало 4, то до этого их было
4 : 2 = 2. Тогда у Оли после второго шага было 8 – 2 = 6 конфет. На первом шаге Женя дал Оле столько конфет, сколько было у Оли. Значит, после первого обмена число конфет у Оли удвоилось. И так как их стало 6, то до этого их было 6 : 2 = 3. Следовательно, в начале у Жени было 8 – 2 = 5 конфет.











































