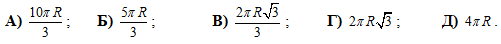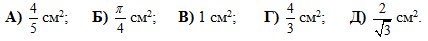Задание 1
|
20 × 19 + 20 + 19 =
A) 389 Б) 399 В) 409 Г) 419 Д) 429
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Поезду детской железной дороги требуется 1 минута 11 секунд, чтобы проехать один круг. Сколько времени ему нужно, чтобы проехать 6 кругов?
A) 6 мин 56 сек
Б) 7 мин 6 сек
В) 7 мин 16 сек
Г) 7 мин 26 сек
Д) 7 мин 36 сек
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Задание 3
|
Парикмахер хочет написать слово SHAVE таким образом, чтобы клиент, смотрящий в зеркало, правильно прочитал это слово, написанное на доске позади его. Как нужно написать это слово на доске?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Задание 4
|
Сколько разных сумм можно получить, бросив три стандартных игральных кубика?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 31.5 - 0.75 = 30.75
|
Задание 5
|
Пять одинаковых стаканов в вариантах ответа заполнены водой. Четыре из них содержат одинаковое количество воды. Какой из них содержит другое количество?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30.75 + 3 = 33.75
|
Задание 6
|
В парке пять ворот. Моника хочет войти через одни ворота и выйти через другие. Сколько у неё существует способов это сделать?
A) 25 Б) 20 В) 16 Г) 15 Д) 10
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 33.75 - 0.75 = 33
|
Задание 7
|
Три кенгуру вместе весят 100 кг. Вес каждого кенгуру измеряется целым числом кг. Все три кенгуру имеют разные веса. Какой наибольший вес может иметь самый лёгкий кенгуру?
A) 1 Б) 30 В) 31 Г) 32 Д) 33
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33 + 3 = 36
|
Задание 8
|
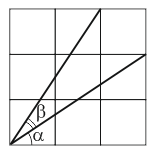
Какое из следующих равенств для углов α и β на рисунке является верным?
A) α = β
Б) 2α + β = 90°
В) α + β = 60°
Г) α + 2β = 90°
Д) α + β = 45°
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 36 + 3 = 39
|
Задание 9
|
В каком из следующих квадратов площадь чёрной части наибольшая?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 39 + 3 = 42
|
Задание 10
|
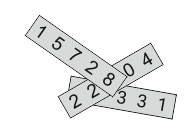
На каждой из трёх полосок бумаги написано пятизначное число (см. рис.). Сумма этих трёх чисел равна 57263. Три цифры скрыты. Какие это цифры?
A) 0, 2 и 2
Б) 1, 2 и 9
В) 2, 4 и 9
Г) 2, 7 и 8
Д) 5, 7 и 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 42 + 3 = 45
|
Задание 11
|
Вершины квадрата ABCD расположены по ходу часовой стрелки. Вершины равностороннего треугольника AEC также расположены по ходу часовой стрелки. Найдите величину угла CBE.
A) 30° Б) 45° В) 135° Г) 1450° Д) 150°
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 45 - 1 = 44
|
Задание 12
|
Пусть a, b, c и d – различные целые числа из множества чисел от 1 до 10 включительно. Какое наименьшее значение может принимать выражение a/b + c/d ?
A) 2/10 Б) 3/19 В) 14/45 Г) 29/90 Д) 25/72
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 44 - 1 = 43
|
Задание 13
|
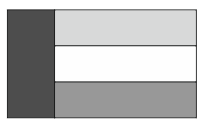
Стороны прямоугольного флага Кенгуру относятся как 3 : 5. Флаг состоит из четырёх прямоугольников одинаковой площади, как показано на рисунке. Как относятся стороны белого прямоугольника?
A) 1 : 3
Б) 1 : 4
В) 2 : 7
Г) 3 : 10
Д) 4 : 15
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 43 + 4 = 47
|
Задание 14
|
Прямоугольник 2х3 можно сложить из уголков

двумя способами:
 и
и 
Сколько существует способов сложить из таких уголков фигуру на следующем рисунке?

A) 1 Б) 2 В) 3 Г) 4 Д) 12
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 47 - 1 = 46
|
Задание 15
|
Триатлон состоит из трёх видов: плавания, бега и велогонки. Велогонка составляет три четверти всей дистанции, бег – одну пятую, а плавание – 2 км. Сколько км составляет вся дистанция в триатлоне?
A) 10 Б) 20 В) 38 Г) 40 Д) 60
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 46 - 1 = 45
|
Задание 16
|
Напиток должен состоять из сока и воды в отношении 1 : 7. Имеется литровая банка, наполовину заполненная соком. Какую часть этого сока нужно использовать, чтобы приготовить 2 литра напитка?
A) 1/4 Б) 1/2 В) 2/7 Г) 4/7 Д) весь сок
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 45 - 1 = 44
|
Задание 17
|
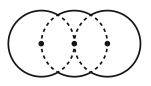
Фигура на рисунке состоит из частей трёх равных кругов радиуса R. Центры кругов находятся на одной прямой, центры крайних кругов – на границе среднего круга. Найдите периметр данной фигуры.
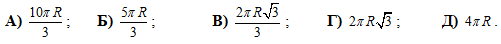
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 44 + 4 = 48
|
Задание 18
|
Сумма цифр семизначного телефонного номера aaabbbb равна двузначному числу ab. Чему равна сумма цифр: a + b?
A) 8 Б) 9 В) 10 Г) 11 Д) 12
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 48 - 1 = 47
|
Задание 19
|
60 яблок и 60 груш нужно упаковать в коробки так, чтобы во всех коробках было поровну яблок, но ни в каких двух коробках не было поровну груш. Какое наибольшее количество коробок может получиться?
A) 20 Б) 15 В) 12 Г) 10 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 47 + 4 = 51
|
Задание 20
|
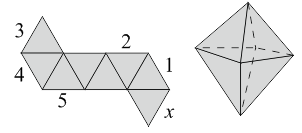
На рисунке показана развёртка поверхности октаэдра. Если её свернуть так, чтобы получился октаэдр, то какое ребро совместится с ребром x?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 51 - 1 = 50
|
Задание 21
|
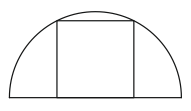
Вершины квадрата находятся на дуге и диаметре полукруга радиуса 1 см, как показано на рисунке. Чему равна площадь квадрата?
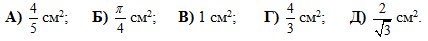
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Задание 22
|
Две точки отмечены на диске, который вращается вокруг своего центра. Одна из точек находится на 3 см дальше от центра диска, чем другая, и движется с постоянной скоростью, которая в 2,5 раза больше, чем скорость другой точки. Каково расстояние от центра диска до дальней точки?
A) 10 см Б) 9 см В) 8 см Г) 6 см Д) 5 см
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
Задание 23
|
Числа от 1 до 99 записаны друг за другом по порядку. Полученную последовательность цифр разбили на тройки:
123456789101112…979899 → (123)(456)(789)(101)(112)…(979)(899).
Какой из следующих троек нет в полученном разбиении?
A) (222) Б) (444) В) (464) Г) (646) Д) (888)
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 47.5 + 5 = 52.5
|
Задание 24
|
Сколько различных плоскостей проходят ровно через три вершины данного куба?
A) 1 Б) 2 В) 4 Г) 8 Д) 12
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 52.5 - 1.25 = 51.25
|
Задание 25
|
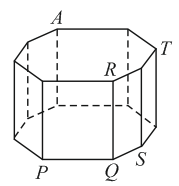
Все рёбра 8-угольной призмы имеют равную длину (см. рис.). В вершине A находится муравей. За 1 секунду он перемещается по ребру в соседнюю вершину. В какой из изображённых вершин муравей может оказаться через 2019 секунд?
A) только в P, R или S
Б) только в P, R, S или T
В) только в Q
Г) только в T
Д) в любой из вершин P, Q, R, S, T
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 51.25 - 1.25 = 50
|
Задание 26
|
Числа A, B и C трёхзначные; первые цифры у них совпадают с последними. Кроме того, выполняются равенства:
B = 2A + 1 и C = 2B + 1.
Сколько различных значений может принимать число A?
A) 0 Б) 1 В) 2 Г) 3 Д) более 3
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Задание 27
|
В вершинах квадрата записаны натуральные числа. При этом выполняются следующие условия. Если два числа находятся на концах стороны квадрата, то одно из них делится на другое. А если два числа расположены на концах диагонали, то ни одно из них не делится на другое. Какое наименьшее значение может иметь сумма этих четырёх чисел?
A) 12 Б) 24 В) 30 Г) 35 Д) 60
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
Задание 28
|
Какое наименьшее количество чисел нужно вычеркнуть из множества {10, 20, 30, 40, 50, 60, 70, 80, 90}, чтобы произведение оставшихся чисел было полным квадратом?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 47.5 + 5 = 52.5
|
Задание 29
|
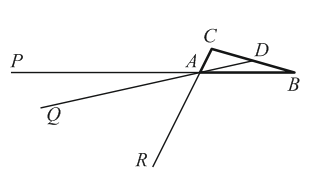
Дан треугольник ABC площади S. Точка D – середина стороны BC. Точки P, Q и R на прямых AB, AD и AC соответственно таковы, что AP = 2 • AB, AQ = 3 • AD и AR = 4 • AC. Чему равна площадь треугольника PQR?
A) S
Б) 2 S
В) 3 S
Г) 0,5 S
Д) 0 (т. е., P, Q и R лежат на одной прямой)
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 52.5 - 1.25 = 51.25
|
Задание 30
|
Сколько четырёхзначных чисел обладает следующим свойством: если вычеркнуть любую цифру данного числа, то получится трёхзначное число, которое является делителем данного четырёхзначного числа?
A) 5 Б) 9 В) 14 Г) 19 Д) 23
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 51.25 - 1.25 = 50
|










 и
и