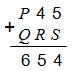"Кенгуру-2018"

15 марта 2018
Задание для 9-10 классов

Участник: Прокопович Оксана, Деревнянская СШ, Столбцовский РООСиТ

На старте каждый участник получает 30 баллов

Задание 1

В нашей семье у каждого ребёнка по крайней мере 2 брата и по крайней мере 1 сестра. Какое наименьшее число детей может быть в нашей семье?

A) 3       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: В

Ответ участника: Б

Промежуточный результат: 30 - 0.75 = 29.25

Задание 2

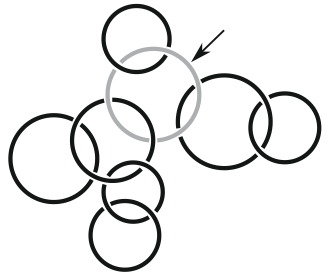
Некоторые из колец на рисунке образуют цепочки. Сколько колец образуют самую длинную цепочку, содержащую серое кольцо (второе сверху)?

A) 3       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: В

Ответ участника: Г

Промежуточный результат: 29.25 - 0.75 = 28.5

Задание 3

Длины двух сторон треугольника равны 5 и 2, а длина третьей стороны – целое нечётное число. Найдите длину третьей стороны треугольника.

A) 3       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: В

Ответ участника: Д

Промежуточный результат: 28.5 - 0.75 = 27.75

Задание 4

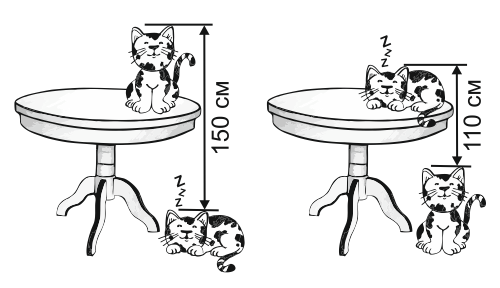
Расстояние от спины кота, спящего на полу, до кончика уха кота, сидящего на столе, составляет 150 см. Расстояние от кончика уха кота, сидящего на полу, до спины кота, спящего на столе, составляет 110 см. Какова высота стола?

A) 110 см       Б) 120 см       В) 130 см       Г) 140 см       Д) 150 см

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 27.75 + 3 = 30.75

Задание 5

Сумма пяти последовательных натуральных чисел равна 10²⁰¹⁸. Чему равно среднее из этих чисел?

A) 10²⁰¹³       Б) 5²⁰¹⁷       В) 10²⁰¹⁷       Г) 2²⁰¹⁸       Д) 2·10²⁰¹⁷

Правильный ответ: Д

Ответ участника: Б

Промежуточный результат: 30.75 - 0.75 = 30

Задание 6

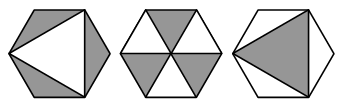
Даны три равных правильных шестиугольника. Пусть X, Y и Z – площади их серых частей (первого, второго и третьего, соответственно). Какое из следующих соотношений верно?

A) X = Y = Z

Б) X ≠ Y = Z

В) Z = X ≠ Y

Г) X = Y ≠ Z

Д) все различны

Правильный ответ: А

Ответ участника: Д

Промежуточный результат: 30 - 0.75 = 29.25

Задание 7

Маша собрала в саду 42 яблока, 60 абрикосов и 90 вишен. Она хочет разделить все их на несколько одинаковых по составу частей, чтобы затем угостить своих друзей. Какое наибольшее количество таких частей у неё может получиться?

A) 3       Б) 6       В) 10       Г) 14       Д) 42

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 29.25 + 3 = 32.25

Задание 8

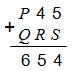
Некоторые из цифр в примере на сложение заменили буквами P, Q, R и S. Чему равна сумма P + Q + R + S?

A) 14       Б) 15       В) 16       Г) 17       Д) 24

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 32.25 + 3 = 35.25

Задание 9

Чему равна сумма 25% от 2018 и 2018% от 25?

A) 1009       Б) 2016       В) 2018       Г) 3027       Д) 5045

Правильный ответ: А

Ответ участника: А

Промежуточный результат: 35.25 + 3 = 38.25

Задание 10

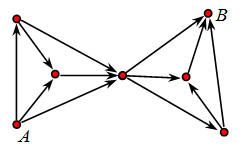
Сколько существует различных путей от пункта A до пункта В на схеме, если передвигаться можно только в направлении стрелок?

A) 20       Б) 16       В) 12       Г) 9       Д) 6

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 38.25 - 0.75 = 37.5

Задание 11

Два здания расположены на одной улице на расстоянии 250 метров друг от друга. В первом здании проживает 100 жителей, а во втором – 150. Где между зданиями нужно установить автобусную остановку, чтобы общее расстояние, которое все жители обоих зданий должны проходить от своих зданий до этой остановки, было бы наименьшим?

A) напротив первого здания

Б) 100 м от первого здания

В) 100 м от второго здания

Г) напротив второго здания

Д) в любой точке между зданиями

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 37.5 - 1 = 36.5

Задание 12

В ряд записали 105 чисел: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, … (каждое число n записано n раз). Сколько из этих чисел делятся на 3?

A) 4       Б) 12       В) 21       Г) 30       Д) 45

Правильный ответ: Г

Ответ участника: В

Промежуточный результат: 36.5 - 1 = 35.5

Задание 13

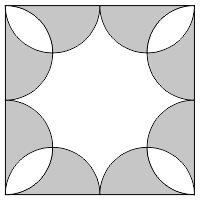
Восемь одинаковых полуокружностей вписаны в квадрат со стороной 4 так, как показано на рисунке. Чему равна площадь белой части квадрата?

A) 2π

Б) 8

В) 6 + π

Г) 3π - 2

Д) 3π

Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 35.5 - 1 = 34.5

Задание 14

Однажды 40 поездов курсировали между пятью городами M, N, O, P и Q. Для каждого из четырёх городов M, N, O и P сумма числа прибывших и числа убывших поездов оказалась равна 10. Чему равна такая же сумма для города Q?

A) 0       Б) 10       В) 20       Г) 30       Д) 40

Правильный ответ: Д

Ответ участника: В

Промежуточный результат: 34.5 - 1 = 33.5

Задание 15

В гуманитарном университете преподают языки, историю и философию. 35% студентов, изучающих языки, изучают английский. 13% студентов университета изучают язык, отличный от английского. Ни один из студентов не изучает более одного языка. Сколько процентов студентов университета изучает языки?

A) 13%       Б) 20%       В) 22%       Г) 48%       Д) 65%

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 33.5 + 4 = 37.5

Задание 16

Петя хотел купить книгу, но денег у него не было. Поэтому он попросил денег у отца и двух братьев. Отец дал ему половину от суммы, которую дали братья. Старший брат дал ему треть от того, что дали остальные. Младший брат дал ему 10 руб. Сколько стоила книга?

A) 24 руб       Б) 26 руб       В) 28 руб       Г) 30 руб       Д) 32 руб

Правильный ответ: А

Ответ участника: Г

Промежуточный результат: 37.5 - 1 = 36.5

Задание 17

Сколько всего существует трёхзначных чисел, обладающих свойством: если стереть среднюю цифру, то получится двузначное число, в 9 раз меньшее исходного?

A) 1       Б) 2       В) 3       Г) 4       Д) 5

Правильный ответ: Г

Ответ участника: В

Промежуточный результат: 36.5 - 1 = 35.5

Задание 18

Сколько слагаемых 2018² расположено под знаком квадратного корня в правильном равенстве

√2018² + 2018² + ... + 2018² = 2018¹⁰ ?

A) 5       Б) 8       В) 18       Г) 2018⁸       Д) 2018¹⁸

Правильный ответ: Д

Ответ участника: А

Промежуточный результат: 35.5 - 1 = 34.5

Задание 19

Сколько цифр имеет число, являющееся значением выражения

10²⁰¹⁸·(10²⁰¹⁸ - 1) : 9 ?

A) 2017       Б) 2018       В) 4035       Г) 4036       Д) 4037

Правильный ответ: Г

Ответ участника: Д

Промежуточный результат: 34.5 - 1 = 33.5

Задание 20

Правильный 2018-угольник с вершинами, пронумерованными по ходу часовой стрелки числами от 1 до 2018, разбили диагоналями на три многоугольника. Одна диагональ соединяет вершины с номерами 18 и 1018, а другая – вершины с номерами 1018 и 2000. Сколько вершин имеют полученные три многоугольника?

A) 38, 983, 1001

Б) 37, 983, 1001

В) 38, 982, 1001

Г) 37, 982, 1000

Д) 37, 983, 1002

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 33.5 - 1 = 32.5

Задание 21

На доске записано несколько целых чисел, включая число 2018. Сумма всех чисел равна 2018. Произведение всех чисел также равно 2018. Какое общее количество чисел может быть записано на доске?

A) 2016       Б) 2017       В) 2018       Г) 2019       Д) 2020

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 32.5 + 5 = 37.5

Задание 22

Даны четыре числа. Рассмотрим сумму одного из них и среднего арифметического трёх других. Такие суммы можно вычислить четырьмя способами, и они равны 17, 21, 23 и 29. Чему равно наибольшее из данных чисел?

A) 12       Б) 15       В) 21       Г) 24       Д) 29

Правильный ответ: В

Ответ участника: Г

Промежуточный результат: 37.5 - 1.25 = 36.25

Задание 23

Точки А₁, А₂, А₃, ... лежат на прямой. Известно, что А₁А₂=1 и для любого натурального n точка А_n является серединой отрезка А_n+1А_n+2. Чему равна длина отрезка А₁А₁₂ ?

A) 171       Б) 341       В) 512       Г) 587       Д) 683

Правильный ответ: Д

Ответ участника: Б

Промежуточный результат: 36.25 - 1.25 = 35

Задание 24

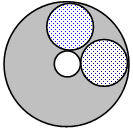
Две концентрические окружности радиуса 1 и 9 образуют кольцо. В кольцо вписали n непересекающихся окружностей, каждая из которых касается внешней и внутренней границы кольца (так, как показано на рисунке, где n = 2). Найдите наибольшее возможное значение n.

A) 1       Б) 2       В) 3       Г) 4       Д) 5

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 35 + 5 = 40

Задание 25

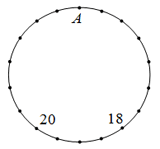
Вася хочет записать числа в вершины правильного 18-угольника так, чтобы каждое число равнялось сумме чисел в двух соседних вершинах. Два числа он уже вписал так, как показано на рисунке. Какое число он должен записать в вершине A?

A) 2018       Б) -20       В) 18       Г) 38       Д) -38

Правильный ответ: Г

Ответ участника: БД

Промежуточный результат: 40 - 1.25 = 38.75

Задание 26

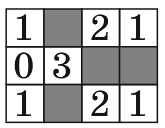
Диана нарисовала прямоугольную таблицу, состоящую из 12 клеток. Некоторые из клеток она окрасила в чёрный цвет. В каждой неокрашенной клетке она записала число соседних с ней по стороне чёрных клеток (см. рис.). Представим, что она сделает то же самое с таблицей, состоящей из 2018 клеток. Какое наибольшее значение может иметь сумма всех чисел в такой таблице?

A) 1262       Б) 2016       В) 2018       Г) 3025       Д) 3027

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 38.75 + 5 = 43.75

Задание 27

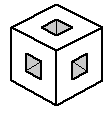
Семь единичных кубиков были удалены из куба 3 × 3 × 3 так, как показано на рисунке. Как выглядит сечение оставшейся части куба, проходящее через его центр перпендикулярно одной из четырёх больших диагоналей?

Правильный ответ: А

Ответ участника: В

Промежуточный результат: 43.75 - 1.25 = 42.5

Задание 28

Петя хочет вписать числа 1, 2, 3, 4, 5 и 6 в таблицу 2 × 3 так, чтобы суммы чисел во всех строчках и всех столбцах были кратны 3. Сколько существует различных способов это сделать?

A) 36       Б) 42       В) 45       Г) 48       Д) другой ответ

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 42.5 - 1.25 = 41.25

Задание 29

Эдуард склеил большой куб из нескольких одинаковых кубиков, а затем он окрасил несколько его граней. Его сестра Николь уронила куб, и он распался на исходные кубики. Ровно 45 из этих кубиков оказались полностью неокрашенными. Сколько граней большого куба окрасил Эдуард?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

Правильный ответ: В

Ответ участника: Г

Промежуточный результат: 41.25 - 1.25 = 40

Задание 30

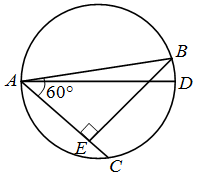
В круге с диаметром AD проведены хорды AB и AC. Известно, что ∠BAC=60°, ВЕ ⊥ АС, АВ=24 см, ЕС=3 см. Найдите длину хорды BD.

A) √3       Б) 2       В) 3       Г) 2√3       Д) 3√2

Правильный ответ: Г

Ответ участника: В

Промежуточный результат: 40 - 1.25 = 38.75

Окончательный результат: 38.75

Место в Беларуси: 4462

Место в области: 695

Место в районе: 31

Место в школе: 2

Участник получает свидетельство и "приз для всех".