Задание 1
|
Чему равно значение выражения (20 + 18) : (20 - 18) ?
A) 18 Б) 19 В) 20 Г) 34 Д) 36
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 2
|
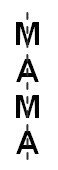
Если буквы слова МАМА записать вертикально, то запись будет иметь вертикальную линию симметрии (см. рис.). Какое из следующих слов обладает таким же свойством?
A) ROOT Б) BOOM В) BOOT Г) LOOT Д) TOOT
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 3
|
Длины сторон треугольника равны 6, 10 и 11 см. Чему равна длина стороны равностороннего треугольника, имеющего такой же периметр?
A) 6 Б) 9 В) 10 Г) 11 Д) 27
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 4
|
Какое число нужно вписать в выражение
2 · 18 · 14 = 6 · ? · 7
вместо знака вопроса, чтобы выражение превратилось в правильное равенство?
A) 8 Б) 9 В) 10 Г) 12 Д) 15
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 5
|

У дедушки в деревне вокруг дома построен красивый забор. Однажды во время бури одна из панелей забора (см. рис.) упала. Какую из показанных в вариантах ответа панелей дедушка увидел упавшей, подойдя к забору?

|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 6
|
Лестница между этажами здания имеет ступеньки высотой 15 см и шириной 15 см. Сколько ступенек нужно преодолеть, чтобы подняться с первого этажа до второго, находящегося на 3 м выше?
A) 8 Б) 10 В) 15 Г) 20 Д) 25
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 7
|
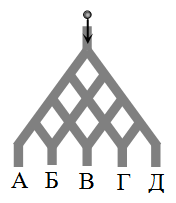
В лабиринт, построенный из трубок, бросают шарик. На каждом разветвлении шарик может продолжить падение по любому из двух возможных направлений. Сколько различных способов падения приводят к выходу Б?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 8
|
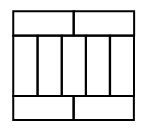
Из девяти одинаковых прямоугольников сложили большой прямоугольник (см. рис.). Чему равен его периметр, если бóльшая сторона маленьких прямоугольников равна 10 см?
A) 40 см Б) 48 см В) 76 см Г) 80 см Д) 90 см
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 9
|
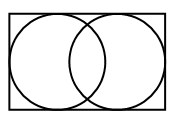
Две окружности вписаны в прямоугольник 7 × 11 так, как показано на рисунке. Найдите расстояние между центрами этих окружностей.
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 10
|
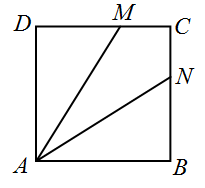
Отрезки AM и AN делят квадрат ABCD со стороной 3 см на три фигуры одинаковой площади (см. рис). Найдите длину BN.
A) 0,5 см Б) 1 см В) 1,5 см Г) 2 см Д) 2,5 см
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 11
|

Маша правильно перемножила два двузначных числа на клетчатой бумаге. Затем три клетки с цифрами она замазала красным фломастером (см. рис.). Чему равна сумма цифр в замазанных клетках?
A) 5 Б) 6 В) 9 Г) 12 Д) 14
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 12
|
Прямоугольная таблица состоит из 40 одинаковых клеток и имеет более одной строки. Андрей нашёл, что в таблице есть средняя строка, и окрасил все её клетки. Сколько клеток при этом оказалось не окрашено?
A) 20 Б) 30 В) 32 Г) 35 Д) 39
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 13
|
Филипп хочет узнать массу книги с точностью до полграмма. Но его весы могут показывать массу только с точностью до 10 граммов. Какое наименьшее количество экземпляров данной книги Филиппу нужно взвесить вместе, чтобы можно было определить массу одного экземпляра с нужной точностью?
A) 5 Б) 10 В) 15 Г) 20 Д) 50
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 14
|
В одной из трёх комнат скрывается лев. На двери первой комнаты написано: «Лев здесь»; на двери второй комнаты: «Лев не здесь», а на двери третьей комнаты: «2 + 3 = 2 × 3». Только одна из надписей является правдивой. В какой комнате скрывается лев?
A) в первой
Б) во второй
В) в третьей
Г) в первой или второй
Д) в любой
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 15
|
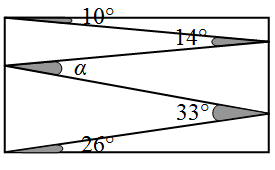
Валерий нарисовал зигзаг внутри прямоугольника так, что получилось несколько углов (см. рис.). Четыре из них равны: 10°, 14°, 33° и 26°. Чему равна величина угла α?
A) 11° Б) 12° В) 16° Г) 17° Д) 33°
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 16
|
Алиса хочет составить список из нескольких простых чисел, меньших 100, используя только цифры 1, 2, 3, 4 и 5, каждую из них ровно один раз. Какое из следующих чисел должно быть в её списке? (Число 1 не является простым.)
A) 2 Б) 5 В) 31 Г) 41 Д) 53
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 17
|
На одном Карибском острове в каждом году 350 солнечных дней. Какое наименьшее число дней нужно провести на этом острове, чтобы наверняка за время пребывания по крайней мере два дня подряд были солнечными? (Считать, что в году 365 дней.)
A) 17 Б) 21 В) 31 Г) 32 Д) 35
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 18
|
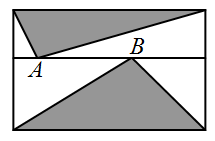
На прямой, параллельной стороне прямоугольника, отмечены точки A и B (см. рис.). Сумма площадей двух серых треугольников равна 10 см2. Чему равна площадь данного прямоугольника?
A) 18 см2
Б) 20 см2
В) 22 см2
Г) 24 см2
Д) зависит от расположения точек A и B
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 19
|

Женя вписал числа 1, 2, 3, …, 9 в клетки таблицы 3 × 3. Затем он вычислил суммы чисел во всех строчках и всех столбцах. Пять из этих сумм оказались равны 12, 13, 15, 16 и 17. Чему равна шестая сумма?
A) 17 Б) 16 В) 15 Г) 14 Д) 13
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 20
|
На горизонтальной прямой отмечено 11 точек. Сумма расстояний от крайней левой точки до других десяти точек равна 2018, а сумма расстояний от второй слева точки до других десяти точек (включая первую) равна 2000. Чему равно расстояние между первой и второй слева точками?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 21
|
Имеется 3 кандидата на пост старосты в параллели 7-х классов: Сергей, Кирилл и Андрей. В голосовании участвуют 130 школьников. В ходе голосования уже получили: Сергей – 24 голоса, Кирилл – 29 голосов и Андрей – 37 голосов. Сколько, по крайней мере, ещё голосов нужно Андрею, чтобы гарантированно победить в выборах? (Староста избирается простым большинством.)
A) 13 Б) 14 В) 15 Г) 16 Д) 17
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 22
|
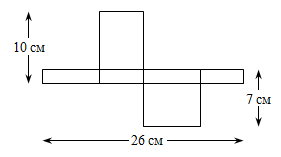
На рисунке показана развёртка прямоугольной коробки. Чему равен объём этой коробки?
A) 43 см3 Б) 70 см3 В) 80 см3 Г) 100 см3 Д) 182 см3
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 23
|
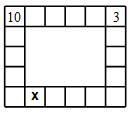
Рита хочет вписать числа во все клетки на рисунке так, чтобы в каждой клетке число равнялось сумме чисел в двух соседних с ней по стороне клетках. Два числа она уже вписала так, как показано на рисунке. Какое число она должна вписать в клетку, отмеченную символом x?
A) 10 Б) 7 В) 13 Г) – 13 Д) – 3
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 24
|
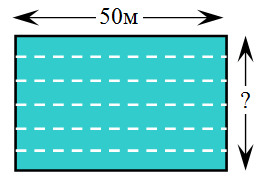
Степан и Иван устроили гонки. Степан бежит по периметру прямоугольного бассейна, а Иван плывёт по дорожке этого бассейна поочерёдно в двух направлениях. Степан бежит в 3 раза быстрее, чем плывёт Иван. За время, которое понадобилось Ивану, чтобы проплыть 6 раз водную дорожку, Степан 5 раз пробежал вокруг бассейна. Чему равна ширина бассейна, если известно, что его длина равна 50 м?
A) 50 м Б) 40 м В) 35 м Г) 30 м Д) 25 м
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 25
|

На клетчатой бумаге изображён «голубь». Его границу составляют отрезки прямых и дуги окружностей. Площадь «голубя» равна 192 см2. Каковы размеры бумаги?
A) 6 см × 4 см
Б) 12 см × 8 см
В) 20 см × 12 см
Г) 24 см × 16 см
Д) 30 см × 20 см
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 26
|

Плитки домино расположены в ряд правильно, если они соприкасаются друг с другом клетками с одинаковым числом точек. Павел выложил в ряд несколько плиток так, как показано на рисунке. За один ход можно поменять местами любые две плитки или перевернуть одну из плиток. За какое наименьшее число таких ходов можно разместить все плитки правильно?
A) 1 Б) 2 В) 3 Г) 4 Д) это невозможно сделать
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 27
|
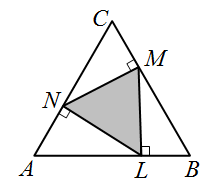
Точки N, M и L – точки на сторонах равностороннего треугольника ABC, такие, что NM ⊥ BC, ML ⊥ AB, LN ⊥ AC (см. рис.). Площадь треугольника ABC равна 36. Чему равна площадь треугольника LMN?
A) 9 Б) 12 В) 15 Г) 16 Д) 18
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 28
|
Аня, Валя и Света совершали покупки в магазине. Валя потратила только 15% от того, что потратила Света, а Аня потратила на 60% больше, чем Света. Вместе три девочки затратили на покупки 55 руб. Сколько затратила на покупки Аня?
A) 3 руб Б) 20 руб В) 25 руб Г) 26 руб Д) 32 руб
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 29
|
Виталий учится прыгать в длину. Сегодня среднее арифметическое длины его прыжков составляет 380 см. Но после очередного прыжка на 399 см это среднее арифметическое стало равным 381 см. Какой должна быть длина ещё одного его прыжка, чтобы среднее арифметическое стало равным 382 см?
A) 397 см Б) 400 см В) 401 см Г) 403 см Д) 404 см
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|
Задание 30
|
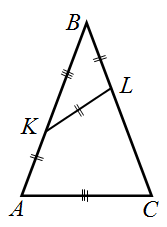
В равнобедренном треугольнике ABC на боковых сторонах AB и BC отмечены точки K и L соответственно. Оказалось, что AK = KL = LB и KB = AC. Найдите величину угла ABC.
A) 30° Б) 35° В) 36° Г) 40° Д) 44°
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
|