Задание 1
|
Какое время будет через 17 часов после 17:00 ?
A) 8:00 Б) 10:00 В) 11:00 Г) 12:00 Д) 13:00
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Несколько девочек стоят по кругу. Лена – четвёртая слева от Яны, она же – седьмая справа от Яны. Сколько девочек стоит по кругу?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Задание 3
|
Какое число нужно вычесть из числа -17, чтобы получить число -33?
A) -50 Б) -16 В) 16 Г) 40 Д) 50
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Задание 4
|
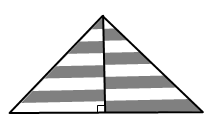
Равнобедренный треугольник на рисунке разбит на полоски равной ширины. Какая его часть является серой?
A) 1/2 Б) 1/3 В) 2/3 Г) 3/4 Д) 2/5
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Задание 5
|
Какое из следующих равенств является правильным?
A) 4/1 = 1,4
Б) 5/2 = 2,5
В) 6/3 = 3,6
Г) 7/4 = 4,7
Д) 8/5 = 5,8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Задание 6
|
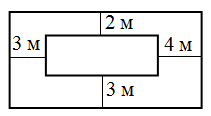
На рисунке показаны два прямоугольника с параллельными сторонами и указаны расстояния между ними. Чему равна разность периметров этих прямоугольников?
A) 12 м Б) 16 м В) 12 м Г) 21 м Д) 24 м
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Задание 7
|

Боря дважды согнул лист бумаги, а затем сделал один прокол. Когда он развернул этот лист, то получил лист, изображенный на рисунке выше. Как Боря сворачивал лист бумаги?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Задание 8
|
Сумма трёх различных натуральных чисел равна 7. Чему равно их произведение?
A) 12 Б) 10 В) 9 Г) 8 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Задание 9
|

Рита сделала декорацию из четырёх красных и белых «сердечек», наклеив их друг на друга (см. рис.). Площади сердечек равны 1 см2, 4 см2, 9 см2 и 16 см2. Чему равна площадь красной части декорации?
A) 9 см2
Б) 10 см2
В) 11 см2
Г) 12 см2
Д) 13 см2
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 46.5 - 0.75 = 45.75
|
Задание 10
|
У Вали есть 20 рублей, а у её четырёх сестёр – по 10 рублей. Сколько рублей Вале нужно дать каждой из своих сестёр, чтобы у всех пяти девочек денег стало поровну?
A) 2 Б) 4 В) 5 Г) 8 Д) 10
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 45.75 + 3 = 48.75
|
Задание 11
|

Божья коровка и муравей ползут по шесту, начав с разных его сторон. Божья коровка проползла 3/4 длины шеста, а муравей – 2/3. Какая часть длины шеста равна расстоянию между ними?
A) 3/8 Б) 1/12 В) 5/7 Г) 1/2 Д) 5/12
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 48.75 - 1 = 47.75
|
Задание 12
|
Среди посетителей детского театра взрослые составили одну шестую часть. Две пятых от общего числа детей составили мальчики. Какую часть от числа всех посетителей составили девочки?
A) 1/2 Б) 1/3 В) 1/4 Г) 1/5 Д) 2/5
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 47.75 + 4 = 51.75
|
По условию задачи взрослые составляют одну шестую часть посетителей театра. Значит, все остальные, то есть дети, составляют 1 - 1/6 = 5/6 от всех посетителей театра. Аналогично, если мальчики составляют 2/5 от общего числа детей, то оставшиеся девочки составляют 1 - 2/5 = 3/5 от общего числа детей. Наконец, если девочки составляют 3/5 детей, а все дети соответствуют 5/6 всех посетителей театра, то девочки представляют собой 3/5 · 5/6 =
3/6 = 1/2 от всех посетителей театра.
Задание 13
|
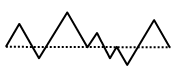
На рисунке чёрная ломаная и штриховой отрезок образуют 7 равносторонних треугольников. Длина штрихового отрезка равна 20 см. Чему равна длина чёрной ломаной?
A) 25 см Б) 30 см В) 35 см Г) 40 см Д) 45 см
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 51.75 - 1 = 50.75
|
Задание 14
|
Сёстрам Эмме, Еве, Рите и Зине 3, 8, 12 и 14 лет, не обязательно в таком же порядке. Эмма моложе Риты. Сумма возрастов Зины и Эммы делится на 5. Сумма возрастов Зины и Риты тоже делится на 5. Сколько лет Еве?
A) 14 Б) 12 В) 8 Г) 5 Д) 3
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 50.75 + 4 = 54.75
|
Задание 15
|
В конкурсе «Кенгуру» в нашем районе приняли участие более 800 школьников. Девочки составили ровно 35% от числа участников, а мальчиков оказалось на 252 человека больше, чем девочек. Сколько всего школьников нашего района участвовало в «Кенгуру»?
A) 802 Б) 810 В) 822 Г) 824 Д) 840
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 54.75 - 1 = 53.75
|
Задание 16
|
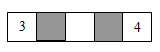
Рита хочет вписать числа во все клетки на рисунке. Два из них она уже вписала. Рита хочет также, чтобы сумма всех чисел равнялась 35, чтобы сумма чисел в первых трёх клетках равнялась 22, а сумма чисел в последних трёх клетках равнялась 25. Чему будет равно произведение чисел в серых клетках?
A) 63 Б) 108 В) 0 Г) 48 Д) 39
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 53.75 + 4 = 57.75
|
Задание 17
|
Симона хочет разрезать ленту на 9 равных частей и отметила на ленте соответствующие точки разрезания. Барбара хочет разрезать эту же ленту на 8 равных частей и также отметила на ней соответствующие точки разрезания. Карл взял и разрезал ленту во всех отмеченных точках. Сколько всего кусков ленты получилось в результате?
A) 15 Б) 16 В) 17 Г) 18 Д) 19
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 57.75 - 1 = 56.75
|
Задание 18
|
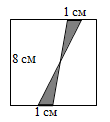
Два отрезка длины 1 см отмечены на противоположных сторонах квадрата со стороной 8 см. Концы отрезков соединили так, как показано на рисунке. Чему равна сумма площадей двух серых треугольников?
A) 2 см2
Б) 4 см2
В) 4,2 см2
Г) 6,4 см2
Д) 8 см2
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 56.75 + 4 = 60.75
|
Задание 19
|
Тихон занимается спортом и составляет график пробежек. Он хочет бегать ровно два раза в неделю в одни и те же дни недели, но так, чтобы не случалось пробежек два дня подряд. Сколько таких различных графиков существует?
A) 16 Б) 14 В) 12 Г) 10 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 60.75 + 4 = 64.75
|
Задание 20
|
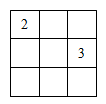
Мария хочет вписать числа в клетки таблицы 3 × 3 так, чтобы суммы чисел в любых двух клетках, имеющих общую сторону, были одинаковы. Она уже вписала два числа так, как показано на рисунке. Чему будет равна сумма всех чисел в таблице?
A) 18 Б) 20 В) 21 Г) 22 Д) 23
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 64.75 - 1 = 63.75
|
Задание 21
|
Все углы треугольника выражаются различными целыми числами градусов. Какое наименьшее значение может иметь сумма меньшего и большего углов такого треугольника?
A) 61° Б) 90° В) 91° Г) 120° Д) 121°
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 63.75 - 1.25 = 62.5
|
Задание 22
|
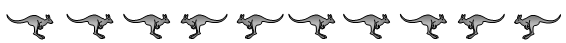
В ряд стоят 10 кенгуру так, как показано на рисунке. В некоторый момент времени какие-то два кенгуру, которые стоят рядом и смотрят друг на друга, меняются местами, но не поворачиваются. Затем снова какие-то два кенгуру, которые стоят рядом и смотрят друг на друга, меняются местами, но не поворачиваются и т.д. Какое число таких перемен мест может быть сделано до того, как они станут невозможны?
A) 15 Б) 16 В) 18 Г) 20 Д) 21
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 62.5 - 1.25 = 61.25
|
Задание 23
|
У Дианы есть 9 чисел: 1, 2, 3, 4, 5, 6, 7, 8 и 9. К некоторым из них она прибавила 2, а к остальным прибавила 5. Какое наименьшее количество различных результатов у неё могло получиться?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 61.25 - 1.25 = 60
|
Задание 24
|
Через каждые 3 минуты из аэропорта к центру города по одному и тому же маршруту одновременно отправляются автобус и маршрутное такси. Автобусу на весь путь требуется 60 минут, а маршрутке – 35 минут. Сколько автобусов обгоняет по пути маршрутка (не считая автобус, с которым она одновременно выезжает)?
A) 8 Б) 9 В) 10 Г) 11 Д) 13
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 60 + 5 = 65
|
Задание 25
|

Скатерть Олеси украшена симметричным узором, показанным на рисунке. Какой процент площади скатерти является чёрным?
A) 16% Б) 24% В) 25% Г) 32% Д) 36%
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 65 - 1.25 = 63.75
|
Задание 26
|
Последовательность 2, 3, 6, 8, 8, … получена следующим образом. Два первых числа равны 2 и 3, каждое следующее число равно последней цифре произведения двух предыдущих чисел. Найдите 2017-й член этой последовательности.
A) 2 Б) 3 В) 4 Г) 6 Д) 8
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 63.75 - 1.25 = 62.5
|
Задание 27
|
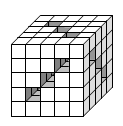
У Миши было 125 одинаковых кубиков. Он склеил из них куб с девятью сквозными прямолинейными тоннелями, как показано на рисунке. Сколько кубиков у него остались не использованными?
A) 52 Б) 45 В) 42 Г) 39 Д) 36
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 62.5 - 1.25 = 61.25
|
Задание 28
|
Два бегуна бегут с постоянной скоростью во встречных направлениях по круговой дорожке длиной 720 метров. Первый бегун пробегает круг за 4 минуты, а второй – за 5 минут. Сколько метров пробегает второй бегун между двумя последовательными встречами с первым бегуном?
A) 355 Б) 350 В) 340 Г) 330 Д) 320
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 61.25 - 1.25 = 60
|
Задание 29
|
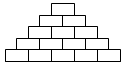
Саша хочет вписать натуральные числа в ячейки на рисунке так, чтобы, начиная со второго снизу ряда, каждое число являлось суммой двух чисел в соседних ячейках, расположенных непосредственно снизу от него. Какое наибольшее количество нечётных чисел может вписать Саша?
A) 5 Б) 7 В) 8 Г) 10 Д) 11
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 60 - 1.25 = 58.75
|
Задание 30
|
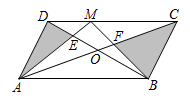
Параллелограмм ABCD на рисунке имеет площадь S. Диагонали пересекаются в точке O. На стороне DC выбрана точка M. Отрезки AM и DB пересекаются в точке E, а отрезки BM и AC – в точке F. Сумма площадей треугольников AED и BFC равна 1/3·S. Чему равна площадь четырехугольника EOFM?
A) 1/6·S
Б) 1/8·S
В) 1/10·S
Г) 1/12·S
Д) 1/14·S
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 58.75 - 1.25 = 57.5
|