"Кенгуру-2016"

17 марта 2016
Задание для 11 классов

Участник: Млынарчик Николай, Языльская СШ, Стародорожский РООСиТ

На старте каждый участник получает 30 баллов

Задание 1

Толе и Жене вместе 23 года, Жене и Андрею – 24, а Андрею и Толе – 25. Сколько лет самому старшему из них?

A) 10       Б) 11       В) 12       Г) 13       Д) 14

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 30 + 3 = 33

Задание 2

Сумма 110 + 1 100 + 1  1000 равна

A)  3 111       Б) 111 1110       В) 111 1000       Г)  3  1000       Д)  3  1110

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 33 + 3 = 36

Задание 3

Маша знает, что расстояние от любой точки любого берега реки до ближайшей точки противоположного берега одно и то же. Какой из следующих рисунков не может быть рисунком данной реки?

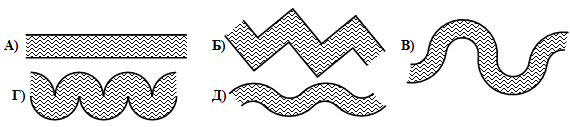
Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 36 + 3 = 39

Задание 4

Сколько существует целых чисел, больших 2015 · 2017, но меньших 2016 · 2016?

A) 0       Б) 1       В) 2       Г) 2015       Д) 2016

Правильный ответ: А

Ответ участника: А

Промежуточный результат: 39 + 3 = 42

Задание 5

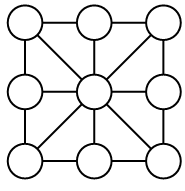
Диана хочет вписать в кружочки диаграммы девять целых чисел так, чтобы суммы чисел в вершинах всех восьми маленьких треугольников с центрами в кружочках, соединённых отрезками, были одинаковы. Какое наибольшее количество различных чисел она может использовать?

A) 1       Б) 2       В) 3       Г) 4       Д) 6

Правильный ответ: В

Ответ участника: Б

Промежуточный результат: 42 - 0.75 = 41.25

Задание 6

Множество точек на координатной плоскости Oxy образует фигуру кенгуру, показанную на рисунке.

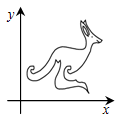
Если каждую точку (a, b) этой фигуры поменять на точку (b, a), то какую фигуру составит новое множество точек?

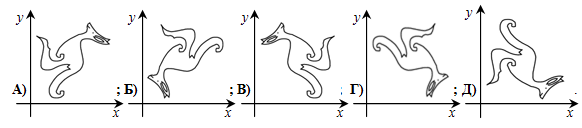
Правильный ответ: А

Ответ участника: Б

Промежуточный результат: 41.25 - 0.75 = 40.5

Задание 7

Какое наименьшее число плоскостей в пространстве необходимо провести, чтобы закрыть со всех сторон ограниченное тело, расположенное в этом пространстве?

A) 3       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 40.5 + 3 = 43.5

Задание 8

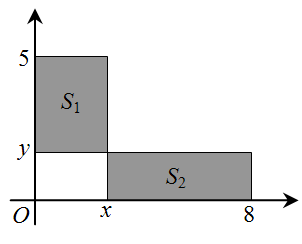
Прямоугольники S₁ и S₂ на координатной плоскости имеют одинаковую площадь (см. рис.). Чему равно отношение x : y ?

A) 1

Б) 3 : 2

В) 4 : 2

Г) 7 : 4

Д) 8 : 5

Правильный ответ: Д

Ответ участника: Б

Промежуточный результат: 43.5 - 0.75 = 42.75

Задание 9

Если x² - 4x + 2 = 0, то x + 2/x равно

A) -4       Б) -2       В) 0       Г) 2       Д) 4

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 42.75 + 3 = 45.75

Задание 10

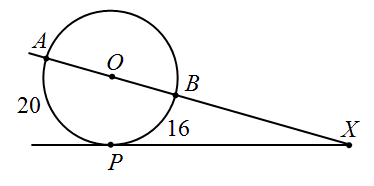
Длины дуг AP и PB на рисунке равны 20 и 16 соответственно; точка O – центр окружности. Найдите величину угла ∠AXP.

A) 30°       Б) 24°       В) 18°       Г) 15°       Д) 10°

Правильный ответ: Д

Ответ участника: А

Промежуточный результат: 45.75 - 0.75 = 45

Задание 11

Натуральные числа a, b, c и d удовлетворяют равенствам

a + 2 = b - 2 = c · 2 = d : 2.

Какое из этих чисел наибольшее?

A) a       Б) b       В) c       Г) d       Д) нельзя определить однозначно

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 45 + 4 = 49

Задание 12

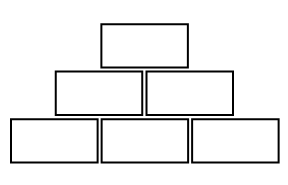
Маша вписывает в прямоугольники на рисунке натуральные числа так, чтобы в каждом из трёх верхних прямоугольников число равнялось произведению чисел в двух соседних нижестоящих прямоугольниках. Какое из следующих чисел не может быть вписано в самом верхнем прямоугольнике, если в прямоугольники нижнего слоя Маша вписала числа, большие 1?

A) 56       Б) 84       В) 90       Г) 105       Д) 220

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 49 - 1 = 48

Задание 13

Найдите значение x₄,   если   x₁ = 2   и   x_n+1 = x_n^x_n   при n ≥ 1.

A) 2²³       Б) 2²⁴       В) 2²¹¹       Г) 2²¹⁶       Д) 2²⁷⁶⁸

Правильный ответ: В

Ответ участника: Д

Промежуточный результат: 48 - 1 = 47

Задание 14

В прямоугольнике ABCD длина диагонали AC вдвое больше стороны BC. На стороне CD выбрана точка M, такая, что AM = MC. Чему равна величина угла ∠CAM?

A) 12,5°       Б) 15°       В) 27,5°       Г) 42,5°       Д) 30°

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 47 + 4 = 51

Задание 15

Диана разрезала прямоугольник площади 2016 на 56 равных квадратов с целыми длинами сторон. Сколько существует различных прямоугольников площади 2016, для которых это можно сделать?

A) 2       Б) 4       В) 6       Г) 8       Д) 0

Правильный ответ: Б

Ответ участника: Г

Промежуточный результат: 51 - 1 = 50

Задание 16

Все жители на острове либо правдивые (всегда говорят правду), либо лжецы (всегда лгут). Путешественник, прибывший на остров, встретил 7 местных жителей, сидящих вокруг костра. Каждый из них сказал: «Оба моих соседа слева и справа – лжецы». Сколько среди них лжецов на самом деле?

A) 3       Б) 4       В) 5       Г) 6       Д) недостаточно данных

Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 50 - 1 = 49

Задание 17

Оба уравнения

x² + ax + b = 0

и

x² + bx + a = 0 (a ≠ b)

имеют действительные корни. Известно, что сумма квадратов корней первого уравнения равна сумме квадратов корней второго уравнения. Чему равна сумма a + b?

A) 0       Б) -2       В) 4       Г) -4       Д) невозможно определить

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 49 + 4 = 53

Задание 18

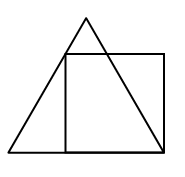
На рисунке изображён квадрат с периметром 4 и равносторонний треугольник. Чему равен периметр этого треугольника?

A) 4

Б) 3 + √3

В) 3

Г) 3 + √2

Д) 4 + √3

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 53 + 4 = 57

Задание 19

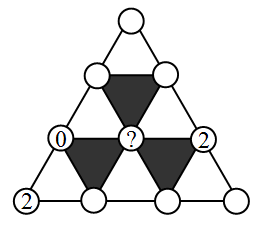
Дядя Игорь хочет вписать в каждую из десяти вершин на рисунке либо 0, либо 1, либо 2, так, чтобы сумма чисел в вершинах любого белого треугольника делилась на 3, а сумма чисел в вершинах любого чёрного треугольника не делилась на 3. Три числа он уже вписал так, как показано на рисунке. Какое из чисел он может вписать в вершину, отмеченную знаком «?»?

A) только 0

Б) только 1

В) только 2

Г) 0 или 1

Д) любое из чисел 0, 1 или 2

Правильный ответ: А

Ответ участника: Б

Промежуточный результат: 57 - 1 = 56

Задание 20

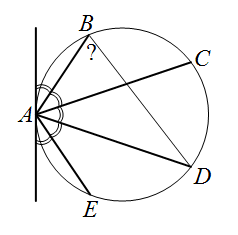
Через точку A проведена окружность и касательная к ней. Точки B, C, D и E лежат на данной окружности так, что пять углов с вершиной A, отмеченных на рисунке, равны между собой. Чему равен угол ∠ABD?

A) 66°       Б) 70,5°       В) 72°       Г) 75°       Д) 77,5°

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 56 + 4 = 60

Задание 21

Сколько действительных решений имеет уравнение

(x² - 4x + 5)^{x2 + x - 30} = 1?

A) 1       Б) 2       В) 3       Г) 4       Д) бесконечно много

Правильный ответ: В

Ответ участника: А

Промежуточный результат: 60 - 1.25 = 58.75

Задание 22

В четырёхугольник вписана окружность. Периметр четырёхугольника относится к длине окружности как 4 : 3. Как относится площадь четырёхугольника к площади круга, ограниченного данной окружностью?

A) 4 : π

Б) 3√2 : π

В) 16 : 9

Г) π : 3

Д) 4 : 3

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 58.75 + 5 = 63.75

Задание 23

Сколько существует квадратичных функций

y = ax² + bx + c,

графики которых проходят по крайней мере через три из отмеченных на координатной плоскости Oxy точки?

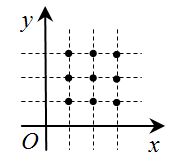
A) 8       Б) 15       В) 19       Г) 22       Д) 27

Правильный ответ: Г

Ответ участника: А

Промежуточный результат: 63.75 - 1.25 = 62.5

Задание 24

В прямоугольном треугольнике биссектрисы острых углов пересекаются в точке P на расстоянии √8 от гипотенузы. Чему равно расстояние от точки P до вершины прямого угла данного треугольника?

A) 8       Б) 3       В) √10       Г) √12       Д) 4

Правильный ответ: Д

Ответ участника: В

Промежуточный результат: 62.5 - 1.25 = 61.25

Задание 25

Три трёхзначных числа состоят из цифр от 1 до 9 (каждая цифра использована ровно один раз). Какое из следующих чисел не может быть суммой этих трёх чисел?

A) 1500       Б) 1503       В) 1512       Г) 1521       Д) 1575

Правильный ответ: А

Ответ участника: А

Промежуточный результат: 61.25 + 5 = 66.25

Задание 26

Внутри куба выбрана точка. Она является вершиной шести пирамид, основаниями которых служат грани куба. Известны объёмы пяти из этих пирамид: 2, 5, 10, 11 и 14. Чему равен объём шестой пирамиды?

A) 1       Б) 4       В) 6       Г) 9       Д) 12

Правильный ответ: В

Ответ участника: Г

Промежуточный результат: 66.25 - 1.25 = 65

Задание 27

Прямоугольная бумажная полоска ABCD ширины 5 см и длины 50 см жёлтая с верхней стороны и синяя – с нижней. Кристина сложила полоску так, что вершина B совместилась с серединой B' стороны CD, а вершина D – с серединой D' стороны AB. Чему равна площадь видимой жёлтой части MD'NB' полоски?

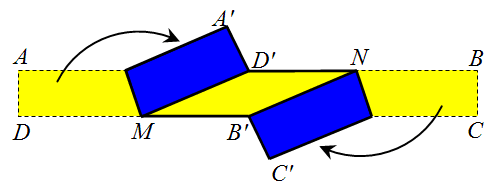
A) 50 см²       Б) 60 см²       В) 62,5 см²       Г) 10 см²       Д) 125 см²

Правильный ответ: Б

Ответ участника: Д

Промежуточный результат: 65 - 1.25 = 63.75

Задание 28

Аня выбрала натуральное число n и вычислила сумму всех натуральных чисел от 1 до n включительно. Затем она нашла простое число p, которое делит эту сумму, но не делит ни одного её слагаемого. Какому из следующих чисел может быть равно значение n + p?

A) 217       Б) 221       В) 229       Г) 245       Д) 269

Правильный ответ: А

Ответ участника: Д

Промежуточный результат: 63.75 - 1.25 = 62.5

Задание 29

Какое наибольшее количество полосок 1 × 3 и 3 × 1 можно расположить на клетчатом квадрате 10 × 10 так, чтобы каждая полоска накрывала в точности 3 клетки и чтобы никакие две из полосок не имели ни одной точки касания?

A) 11       Б) 12       В) 13       Г) 14       Д) 15

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 62.5 - 1.25 = 61.25

Задание 30

Натуральное число N имеет ровно 6 различных натуральных делителей, включая 1 и N. Произведение пяти из них равно 648. Какому числу равен шестой делитель?

A) 4       Б) 8       В) 9       Г) 12       Д) 24

Правильный ответ: В

Ответ участника: Г

Промежуточный результат: 61.25 - 1.25 = 60

Окончательный результат: 60

Место в Беларуси: 569

Место в области: 95

Место в районе: 4

Место в школе: 1

Участник получает свидетельство и "приз для всех".