Задание 1
|
Среднее арифметическое четырёх чисел равно 9. Три из этих чисел – это 5, 9 и 12. Чему равно четвёртое число?
A) 6 Б) 8 В) 9 Г) 10 Д) 36
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Какое из следующих чисел ближе всего к значению выражения 17 × 0,3 × 20,16 : 999?
A) 0,01 Б) 0,1 В) 1 Г) 10 Д) 100
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 33 + 3 = 36
|
Задание 3
|
Рита ответила на все 30 вопросов теста. Число правильных ответов оказалось на 50% больше числа неправильных. На сколько вопросов она ответила правильно?
A) 10 Б) 12 В) 15 Г) 18 Д) 20
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 36 - 0.75 = 35.25
|
Задание 4
|
Четыре из точек в вариантах ответа являются вершинами квадрата. Какая из точек лишняя?
A) (-1;3) Б) (0;-4) В) (-2;-1) Г) (1;1) Д) (3;-2)
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Задание 5
|
Остаток при делении натурального числа x на 6 равен 3. Чему равен остаток при делении числа 3x на 6?
A) 4 Б) 3 В) 2 Г) 1 Д) 0
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
Задание 6
|
Сколько недель составляют 2016 часов?
A) 6 Б) 8 В) 10 Г) 12 Д) 16
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.5 + 3 = 40.5
|
Задание 7
|
Маленький Лукас изобрёл свой собственный способ представления целых отрицательных чисел (представление целых неотрицательных чисел у него – обычное). Считая целые числа в порядке убывания, он пишет 2, 1, 0, 00, 000, 0000, … . Чему равен в его представлении результат 000 + 0000?
A) 1 Б) 00000 В) 000000 Г) 0000000 Д) 00000000
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 40.5 - 0.75 = 39.75
|
Задание 8
|
У меня есть необычные игральные кубики: чётные числа на гранях считаются как обычно, а нечётные – со знаком «минус». Какой из следующих результатов выпадения моих двух кубиков невозможен?
A) 3 Б) 4 В) 5 Г) 7 Д) 8
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 39.75 - 0.75 = 39
|
Задание 9
|
Какое наименьшее число раз нужно поменять местами две соседние буквы, чтобы из слова КУБА получить слово БАКУ?
A) 3 Б) 4 В) 5 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Задание 10
|
Сева выбрал пять различных ненулевых цифр. Он заметил, что сумма никаких двух из них не равна 10. Какое из следующих чисел наверняка присутствует среди этих выбранных цифр?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
|
Задание 11
|
Пусть a + 5 = b2 - 1 = c2 + 3 = d - 4. Какое из чисел a, b, c, d наибольшее?
A) a
Б) b
В) c
Г) d
Д) невозможно определить
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 38.25 - 1 = 37.25
|
Задание 12
|
В две диагонально противоположные клетки квадрата 3×3 вписаны окружности. Найдите расстояние между ближайшими точками этих окружностей.

A) 2√2 - 1
Б) √2 + 1
В) 2√2
Г) 2
Д) 3
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 37.25 - 1 = 36.25
|
Задание 13
|
В теннисном турнире с выбыванием результаты шести из семи игр в четвертьфинале, полуфинале и финале (не обязательно в указанном порядке): Белла победила Анну, Валя победила Диану, Жанна победила Полину, Жанна победила Валю, Валя победила Беллу и Эмма победила Риту. Какой из результатов игр в этих этапах пропущен?
A) Жанна победила Беллу
Б) Валя победил Анну
В) Эмма победила Валю
Г) Белла победила Полину
Д) Жанна победила Эмму
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 36.25 - 1 = 35.25
|
Задание 14
|
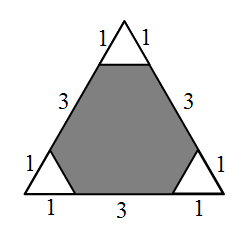
Какая часть площади треугольника на рисунке является серой?
A) 80%
Б) 85%
В) 88%
Г) 90%
Д) невозможно определить
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 35.25
|
Задание 15
|
Женя составляет супермагический квадрат, вписывая числа 1, 2, 4, 5, 10, 20, 25, 50 и 100 в клетки таблицы так, чтобы произведения чисел во всех строчках, всех столбцах и в двух диагоналях были одинковы. Если два числа Женя вписал, как показано на рисунке, то какое число должно быть вписано в серую клетку?
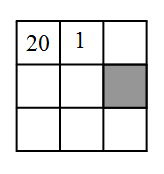
A) 2 Б) 4 В) 5 Г) 10 Д) 25
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 35.25 - 1 = 34.25
|
Задание 16
|
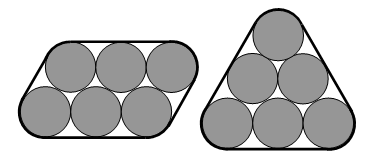
Джек двумя способами связал нитками по 6 одинаковых круглых карандашей диаметра 2 см каждый (см. рис.). Какое из следующих высказываний о длине связывающих ниток является верным?
A) слева на π см короче
Б) слева на 4 см короче
В) справа на π см короче
Г) справа на 4 см короче
Д) обе одинаковой длины
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 34.25 - 1 = 33.25
|
Задание 17
|
В коробке находятся восемь карточек с числами 1, 2, 4, 8, 16, 32, 64 и 128. Ева случайным образом вытащила из коробки несколько карточек, Алла взяла остальные карточки. Сумма чисел на карточках Евы оказалась на 31 больше суммы чисел на карточках Аллы. Сколько карточек вытащила из коробки Ева?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33.25 + 4 = 37.25
|
Задание 18
|

Петя хочет покрасить клетки квадрата 3×3 в разные цвета так, чтобы в каждой строчке, в каждом столбце и на каждой из двух диагоналей все три клетки были разного цвета. Какое наименьшее число различных красок ему для этого понадобится?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 37.25
|
Задание 19
|
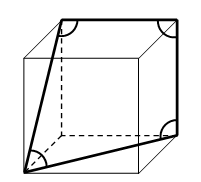
На рисунке изображён куб и отмечено четыре угла. Чему равна их сумма?
A) 315° Б) 330° В) 345° Г) 360° Д) 375°
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 37.25 - 1 = 36.25
|
Задание 20
|
Имеется 2016 кенгуру двух цветов: серого или коричневого (каждого цвета не менее одного кенгуру). Для каждого кенгуру K рассмотрим дробь, в числителе которой – число всех кенгуру другого цвета, отличного от цвета K, а в знаменателе – число всех кенгуру такого же цвета, как K (включая K). Чему может равняться сумма всех таких 2016 дробей?
A) 2016
Б) 1344
В) 1008
Г) 672
Д) недостаточно данных, чтобы определить однозначно
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 36.25 - 1 = 35.25
|
Задание 21
|
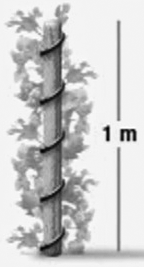
Плющ ровно 5 раз опоясывает столб, который имеет высоту 1 метр и периметр поперечного сечения 15 см. Какую наименьшую длину может иметь такой плющ?
A) 0,75 м Б) 1 м В) 1,25 м Г) 1,5 м Д) 1,75 м
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 35.25
|
Задание 22
|
Какой наибольший остаток можно получить, если разделить двузначное число на сумму его цифр?
A) 13 Б) 14 В) 15 Г) 16 Д) 17
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 35.25 - 1.25 = 34
|
Задание 23
|
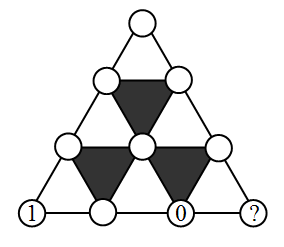
Серёжа хочет вписать в каждую из десяти вершин на рисунке либо 0, либо 1, либо 2, так, чтобы сумма чисел в вершинах любого белого треугольника делилась на 3, а сумма чисел в вершинах любого чёрного треугольника не делилась на 3. Два числа (1 и 0) он уже вписал так, как показано на рисунке. Какое из чисел он может вписать в вершину, отмеченную знаком «?»?
A) только 0
Б) только 1
В) только 2
Г) 0 или 1
Д) любое из чисел 0, 1 или 2
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 34 - 1.25 = 32.75
|
Задание 24
|
Расстояние от пункта A до пункта B вниз по течению реки моторная лодка проходит за 4 часа, а обратно, против течения реки – за 6 часов. За сколько часов доплывёт от пункта A до пункта B деревянный плот?
A) 5 Б) 10 В) 12 Г) 20 Д) 24
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 32.75 + 5 = 37.75
|
Задание 25
|
В республике Кенгуру каждый месяц состоит из 40 дней, которые нумеруются числами от 1 до 40. Каждый день, номер которого делится на 6, является выходным, а каждый день, номер которого является простым числом, является праздничным, остальные дни – рабочие. Сколько в течение месяца существует рабочих дней, у которых предыдущий и последующий дни не являются рабочими?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 37.75 - 1.25 = 36.5
|
Задание 26
|
Две высоты треугольника равны 10 см и 11 см. Какой из следующих не может быть длина третьей высоты?
A) 5 см Б) 6 см В) 7 см Г) 10 см Д) 100 см
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 36.5 - 1.25 = 35.25
|
Задание 27
|
Яков выбрал четыре последовательных натуральных числа. Затем он вычислил все четыре суммы этих чисел по три. Ни одна из сумм не оказалась равной простому числу. Какое наименьшее значение может быть у наименьшего из четырёх выбранных чисел?
A) 12 Б) 10 В) 7 Г) 6 Д) 3
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 35.25 + 5 = 40.25
|
Задание 28
|
За круглым столом ужинают 4 персоны, которые занимаются только одним из следующих видов спорта: лыжи, коньки, биатлон и сноуборд. Персона, занимающаяся лыжами, сидит слева от Ани. Персона, занимающаяся коньками, сидит напротив Богдана. Ева и Филипп сидят рядом. Слева от персоны, занимающейся биатлоном, сидит девушка. Каким видом спорта занимается Ева?
A) коньки Б) лыжи В) биатлон Г) сноуборд Д) недостаточно сведений
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 40.25 - 1.25 = 39
|
Задание 29
|
Дату можно записывать в формате ДД.ММ.ГГГГ. Например, 17.03.2016 означает 17 марта 2016 года, а 03.12.2019 – 3 декабря 2019 года. Будем называть дату интересной, если её запись в указанном формате не содержит одинаковых цифр. В каком месяце, начиная с данного момента, будет ближайшая интересная дата в нынешнем тысячелетии?
A) март Б) июнь В) июль Г) август Д) декабрь
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 39 - 1.25 = 37.75
|
Задание 30
|
Для участия в марафоне прибыло 2016 спортсменов. При регистрации им присвоили номера от 1 до 2016. Перед стартом некоторые из участников обменялись рукопожатиями. При этом каждый из участников с номерами от 1 до 2015 пожал руку такому числу участников, каков его номер. Какому числу участников пожал руку участник с номером 2016?
A) 1 Б) 504 В) 672 Г) 1008 Д) 2015
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.75 + 5 = 42.75
|











