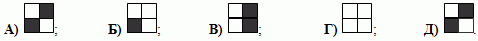Задание 1
|
Какой из следующих дорожных знаков имеет наибольшее число осей симметрии?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Миша разрезал пиццу на 4 равные части, затем каждую из них он разрезал на 3 равных куска. Какую часть пиццы составляет один кусок?
A) третью Б) четвёртую В) седьмую Г) восьмую Д) двенадцатую
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33 + 3 = 36
|
Задание 3
|
Нить длины 10 см сложили равными частями, как показано на рисунке, и разрезали в указанных местах. Какой длины получились куски?

A) 2 см, 3 см и 5 см
Б) 2 см, 2 см и 6 см
В) 1 см, 4 см и 5 см
Г) 1 см, 3 см и 6 см
Д) 3 см, 3 см и 4 см
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 36 + 3 = 39
|
Задание 4
|
На холодильнике Лизы 8 магнитов (чёрные кружочки на рисунке) удерживают 7 открыток. Какое наибольшее число магнитов можно убрать так, чтобы ни одна открытка не упала на пол?
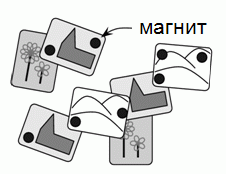
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Задание 5
|
Катя нарисовала квадрат со стороной 10 см. Затем она соединила середины сторон этого квадрата так, что получился меньший квадрат. Чему равна площадь меньшего квадрата?
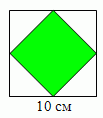
A) 10 см2 Б) 20 см2 В) 25 см2 Г) 40 см2 Д) 50 см2
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
Задание 6
|
У многоножки 100 ножек и 25 пар ботинок. Сколько ещё ботинок ей не хватает, чтобы можно было на каждую ножку одеть по ботинку?
A) 15 Б) 20 В) 35 Г) 50 Д) 75
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.5 + 3 = 40.5
|
Задание 7
|
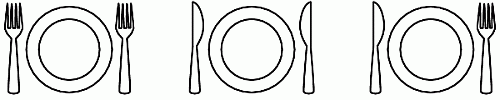
Алиса разложила ножи и вилки на столе так, как показано на рисунке. Но мама сказала ей, что справа от каждой тарелки должен лежать нож, а слева – вилка. Какое наименьшее число раз Алиса должна поменять местами нож и вилку, чтобы все предметы лежали правильно?
A) 1 Б) 2 В) 3 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Задание 8
|
Том и Джон построили прямоугольные блоки, оба из одинакового количества равных кубиков. На рисунке показан блок Тома и нижний слой блока Джона. Сколько слоёв имеет блок, построенный Джоном?
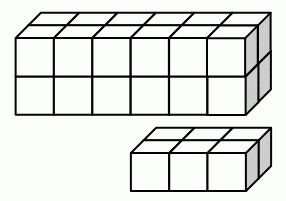
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 43.5 - 0.75 = 42.75
|
Задание 9
|
В детском саду в левой части спальни спят Аня и Валя, повернувшись друг к другу, а в правой части – Галя и Оля, отвернувшись друг от друга (см. рис.). Сколько из этих девочек спят на правом боку?
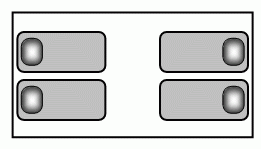
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 42.75 + 3 = 45.75
|
Задание 10
|
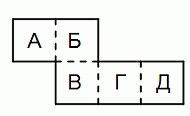
Лист картона, показанный на рисунке, согнули по пунктирным линиям так, что получилась коробка, открытая сверху. Какая из клеток оказалась дном этой коробки?
A) А Б) Б В) В Г) Г Д) Д
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 45.75 + 3 = 48.75
|
Задание 11
|
Какую из следующих фигур нельзя получить, склеив два одинаковых квадратных листа бумаги?
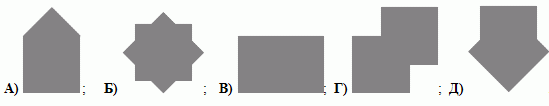
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 48.75 + 4 = 52.75
|
Задание 12
|
Аня, Валя и Галя ходят в детский сад, который работает 5 дней в неделю (с понедельника по пятницу). Аня ходит 3 раза в неделю, а Валя – 4 раза. Каждый рабочий день в саду встречаются ровно 2 из этих девочек. Сколько раз в неделю ходит в детский сад Галя?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 52.75 - 1 = 51.75
|
Задание 13
|
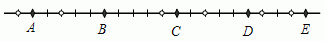
Пять бе́лок A, B, C, D и E (отмечены на рисунке чёрными ромбиками) и 6 орехов (отмечены белыми кружочками) находятся на одной прямой, как показано на рисунке. Белки одновременно с одинаковой скоростью начинают бежать, каждая к ближайшему ореху. Затем, мгновенно съев его, каждая бежит к следующему ближайшему ореху. Какой из белок достанется больше всего орехов?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 51.75 + 4 = 55.75
|
Задание 14
|
В классе за партами парами сидят 30 учащихся. Каждый мальчик сидит с девочкой, но с мальчиками сидит только половина девочек. Сколько мальчиков в этом классе?
A) 25 Б) 20 В) 15 Г) 10 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 55.75 + 4 = 59.75
|
Задание 15
|
На полоске бумаги записано число 2581953764. Женя разрезал полоску в двух местах и получил три полоски с тремя числами. Какое наименьшее значение может иметь сумма этих трёх чисел?
A) 2675 Б) 2975 В) 2978 Г) 4217 Д) 4298
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 59.75 - 1 = 58.75
|
Задание 16
|
Барт посмотрел на зеркало и увидел в нём часы (см. рис.).

Что бы он увидел в зеркале, если бы посмотрел на него 10 минут ранее?

|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 58.75 - 1 = 57.75
|
Задание 17
|
Бабушка купила кошачьего корма для своих четырёх котов с расчётом, чтобы его хватило ровно на 12 дней. Но по дороге домой она подобрала двух беспризорных котов. Если бабушка будет кормить каждого из теперь уже шестерых котов как обычно, то на сколько дней ей хватит купленного корма?
A) 10 Б) 9 В) 8 Г) 6 Д) 4
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 57.75 - 1 = 56.75
|
Задание 18
|
В слове BENJAMIN буквы заменили цифрами 1, 2, 3, 4, 5, 6 и 7 (разные буквы заменили разными цифрами, одинаковые – одинаковыми). Получилось нечётное число, кратное 3. Какой цифрой заменили букву N?
A) 1 Б) 2 В) 3 Г) 5 Д) 7
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 56.75 - 1 = 55.75
|
Задание 19
|
Тим, Том и Джон – тройняшки (родились в один день). У них есть брат, который младше их на 3 года. Какое из следующих чисел может быть суммой лет всех четырёх братьев?
A) 53 Б) 54 В) 56 Г) 59 Д) 60
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 55.75 + 4 = 59.75
|
Задание 20
|
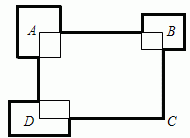
Периметр прямоугольника ABCD равен 30 см. Три других прямоугольника расположены так, что их стороны параллельны сторонам данного прямоугольника и центры совпадают с вершинами A, B и D (см. рис.). Сумма их периметров равна 20 см. Чему равна длина жирной линии?
A) 50 см
Б) 45 см
В) 40 см
Г) 35 см
Д) невозможно определить
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 59.75 - 1 = 58.75
|
Задание 21
|
Аня согнула круглый лист бумаги 3 раза и отрезала кусок (см. рис.). Что она увидит, если развернёт лист?
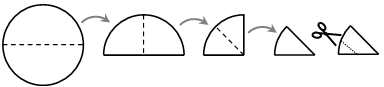

|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 58.75 - 1.25 = 57.5
|
Задание 22
|
Толя записал все числа со следующим свойством: первая цифра равна 1, каждая следующая цифра не меньше предыдущей, сумма всех цифр равна 5. Сколько чисел записал Толя?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 57.5 + 5 = 62.5
|
Задание 23
|
Какое наибольшее число фигур вида 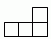 можно вырезать из квадрата 5x5?
можно вырезать из квадрата 5x5?

A) 2 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 62.5 - 1.25 = 61.25
|
Задание 24
|
Луиджи решил открыть ресторан. В связи с этим его друг Джакомо подарил Луиджи несколько квадратных столов и несколько стульев. Если вокруг каждого стола ставить по 4 стула, то 6 стульев не хватит. А если сдвинуть столы парами (число подаренных столов чётное) и ставить вокруг каждой пары столов 6 стульев, то 4 стула окажутся лишними. Сколько столов подарил Джакомо своему другу Луиджи?
A) 8 Б) 10 В) 12 Г) 14 Д) 16
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 61.25 - 1.25 = 60
|
Задание 25
|
Клара хочет сложить треугольник из маленьких треугольных плиток. Она уже расположила несколько плиток так, как показано на рисунке. Какое наименьшее число плиток ей ещё нужно добавить, чтобы завершить построение?
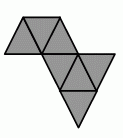
A) 5 Б) 9 В) 12 Г) 15 Д) 18
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 60 + 5 = 65
|
Задание 26
|
Куб построен из 8 чёрных и белых кубиков одного и того же размера. На рисунке показаны пять граней построенного куба.

Как выглядит его шестая грань?
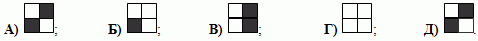
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 65 - 1.25 = 63.75
|
Задание 27
|
Кристина хочет вписать числа в кружочки на сторонах пятиугольника так, чтобы суммы чисел на всех его сторонах оказались равными между собой. Пять чисел она уже вписала так, как показано на рисунке. Какое число ей необходимо вписать в серый кружочек?
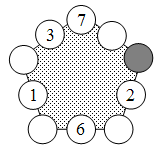
A) 7 Б) 8 В) 11 Г) 13 Д) 15
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 63.75 - 1.25 = 62.5
|
Задание 28
|
Символами ▲, ■ и ● обозначены три различные цифры. Известно, что сумма цифр трёхзначного числа ●■● равна двузначному числу ■▲, а сумма цифр двузначного числа ■▲ равна ■. Какая цифра обозначена символом ●?
A) 4 Б) 5 В) 6 Г) 8 Д) 9
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 62.5 - 1.25 = 61.25
|
Задание 29
|
Кенгурёнок играет с калькулятором. Он начинает с числа 12 и умножает либо делит его на 2 или на 3. С полученным результатом он снова проделывает одну из этих операций и т.д. (Операция деления выполняется только при условии, что получится целый результат). Какое из следующих чисел он не может получить, выполнив 60 таких операций?
A) 12 Б) 18 В) 36 Г) 72 Д) 108
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 61.25 - 1.25 = 60
|
Задание 30
|
Все 6 цифр у двух трёхзначных чисел различны. Первая цифра первого числа в два раза больше последней цифры второго числа. Какое наименьшее значение может иметь сумма таких двух чисел?
A) 552 Б) 546 В) 301 Г) 535 Д) 537
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 60 - 1.25 = 58.75
|
Последняя цифра второго числа не может быть цифрой 0, иначе бы первое число начиналось цифрой 0, что невозможно. Если последняя цифра второго числа – цифра 1, то, согласно условию, первая цифра первого числа – цифра 2. Поскольку у чисел все цифры различны и число не может начинаться цифрой 0, наименьшее значение первой цифры второго числа – это 3. А тогда наименьшая сумма цифр во втором разряде данных двух чисел – это 0 + 4 = 4. В результате, в этом случае наименьшая сумма двух чисел, удовлетворяющих условию задачи, равна 301 + 245 = 546.
Если последняя цифра второго числа – цифра 2, то первая цифра первого числа – цифра 4. Тогда наименьшая цифра второго числа – это 1. А тогда наименьшая сумма цифр во втором разряде данных двух чисел – это 0 + 3 = 3. В результате, в этом случае наименьшая сумма двух чисел, удовлетворяющих условию задачи, равна 102 + 435 = 537, что меньше, чем в первом случае.
Если же последняя цифра второго числа – цифра 3 или больше, то первая цифра первого числа – цифра 6 или больше, и, значит, сумма двух чисел, удовлетворяющих условию, заведомо больше, чем в первых двух случаях.
Таким образом, наименьшая сумма – это сумма Д) 537.







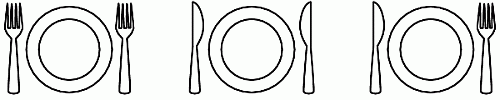



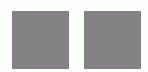
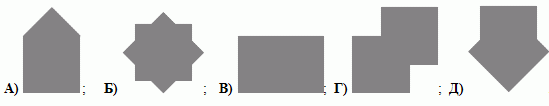
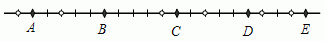





 можно вырезать из квадрата 5x5?
можно вырезать из квадрата 5x5?