Задание 1
|
Какой из букв, записанных на карточках, нет в слове КЕНГУРУ?

A) Л Б) Г В) К Г) И Д) Р
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 24 + 3 = 27
|
Задание 2
|
Сколько верёвок на рисунке?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 27 - 0.75 = 26.25
|
Задание 3
|
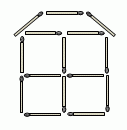
Миша построил из спичек дом, показанный на рисунке. Сколько спичек ему для этого понадобилось?
A) 19 Б) 18 В) 17 Г) 15 Д) 13
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 26.25 + 3 = 29.25
|
Задание 4
|
Сначала в морской лагуне обитало только 2 морских конька, 1 морская звезда и 3 черепахи. Затем в лагуну приплыли ещё 5 морских коньков, 3 морские звезды и 4 черепахи. Сколько всего обитателей стало в лагуне?
A) 6 Б) 9 В) 12 Г) 15 Д) 18
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Задание 5
|
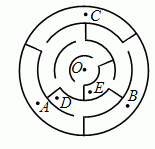
До какой из следующих точек в лабиринте можно добраться, начав путь из точки О?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: В
|
Ответ участника: ВД
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Задание 6
|
К Ване на день рождения пришло 10 детей. Шестеро из них были девочки. Сколько всего было мальчиков на дне рождения?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 31.5 + 3 = 34.5
|
Задание 7
|
Дома́ на улице пронумерованы числами 1, 2, 3, 4 и так далее. Почтальон доставил телеграммы во все дома с номерами от 25 до 57 включительно. Во сколько всего домов были доставлены им телеграммы?
A) 31 Б) 32 В) 33 Г) 34 Д) 35
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
Задание 8
|
Какая из следующих фигур построена из 10 кубиков?
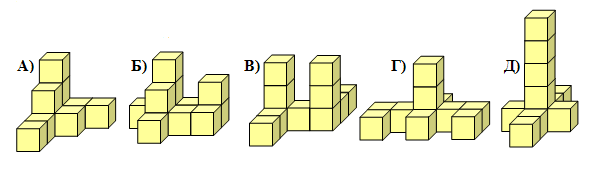
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 33.75 - 0.75 = 33
|
Задание 9
|
Соня раскладывает чёрные и белые шарики на ступеньках лестницы определённым образом (см. рис.). Как будут разложены ею шарики на ступеньке, отмеченной знаком «?»?
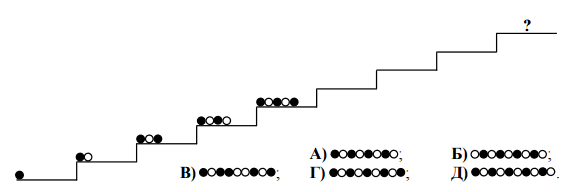
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 33 - 1 = 32
|
Задание 10
|
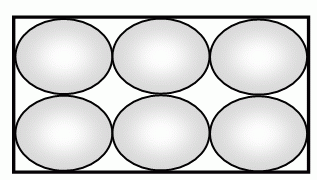
У бабушки в деревне куры несут белые и коричневые яйца. Бабушка положила 6 яиц в коробку (см. рис.) так, что никакие два коричневых яйца не касаются друг друга. Какое наибольшее количество коричневых яиц могло оказаться в коробке?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32 + 4 = 36
|
Задание 11
|
Кенгурёнку сейчас ровно 1 год и 3 месяца. Через сколько месяцев кенгурёнку исполнится 3 года?
A) 9 Б) 18 В) 20 Г) 21 Д) 22
|
Правильный ответ: Г
|
Ответ участника: АВ
|
Промежуточный результат: 36 - 1 = 35
|
Задание 12
|
Бабушка вышла во двор и позвала к себе всех своих кур и своего кота. Все они прибежали к ней, а всего к бабушке прибежало 20 ног. Сколько кур у бабушки?
A) 11 Б) 9 В) 8 Г) 6 Д) 4
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 35 - 1 = 34
|
Задание 13
|
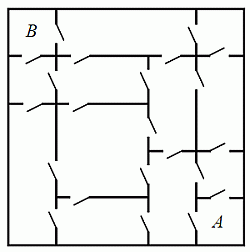
В доме Кошки-Крошки двери в комнатах расположены так, как показано на рисунке. Крошка хочет пройти из комнаты A в комнату B. Какое наименьшее количество дверей ей придётся пройти?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 34 - 1 = 33
|
Задание 14
|
В здании 12 комнат. В каждой комнате имеется 2 окна и проведено электрическое освещение. Вчера вечером 18 окон этого здания было освещено. Сколько комнат было без света?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 33 - 1 = 32
|
Задание 15
|
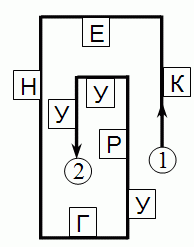
Мария идёт по дороге и читает буквы, встречающиеся по пути справа от неё. Что она прочтёт, пройдя от точки 1 до точки 2?
A) КНУУ Б) КНГУ В) КНР Г) ЕГРУ Д) КЕУ
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 32 - 1 = 31
|
Задание 16
|
Саше и Паше вместе 12 лет. Сколько лет им будет вместе через 4 года?
A) 16 Б) 17 В) 18 Г) 19 Д) 20
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 31 - 1 = 30
|
Задание 17
|
Какая из следующих фигур не может быть сложена из фигурок вида  ?
?

|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 30 - 1.25 = 28.75
|
Задание 18
|
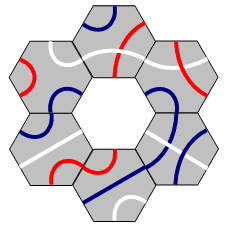
Какую из следующих плиток можно вставить в центр мозаики на рисунке так, чтобы одинаковые линии продолжали друг друга?
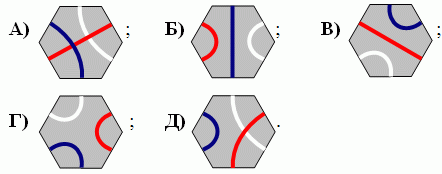
|
Правильный ответ: А
|
Ответ участника: ГД
|
Промежуточный результат: 28.75 - 1.25 = 27.5
|
Задание 19
|
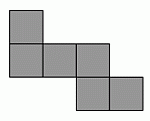
Маша построила из маленьких квадратных плиток фигуру на рисунке. Какое наименьшее число таких плиток ей ещё нужно добавить, чтобы получился большой квадрат, состоящий из этих плиток?
A) 6 Б) 8 В) 9 Г) 10 Д) 12
|
Правильный ответ: Г
|
Ответ участника: АД
|
Промежуточный результат: 27.5 - 1.25 = 26.25
|
Задание 20
|

Пять воробьёв сидят на проводе так, как показано на рисунке. Одни из них смотрят налево, остальные – направо. Каждый воробей чирикнул один раз каждому из воробьёв, сидящих на той стороне, куда он смотрит. Например, третий воробей чирикнул 2 раза. Сколько всего раз чирикнули эти воробьи?
A) 6 Б) 8 В) 9 Г) 10 Д) 12
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 26.25 + 5 = 31.25
|
Задание 21
|

Какую из картинок ответов можно получить из пяти бумажных фигурок на рисунке сверху, наложив их друг на друга?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 31.25 + 5 = 36.25
|
Задание 22
|

Божьи коровки на рисунке собираются сесть на цветки в вариантах ответа. При этом должны выполняться условия: разность между числом точек на правом и левом крыльях божьей коровки совпадает с числом листьев цветка, на который садится божья коровка, а сумма числа точек – с числом его лепестков. На какой из цветков не может сесть ни одна из этих божьих коровок?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 36.25 - 1.25 = 35
|
Задание 23
|
На каждой из шести граней куба изображён один из следующих символов: ♣, ♦, ♥, ♠, ■ и ●; на разных гранях – разные символы. На рисунке показан вид куба с двух разных сторон. Какой символ расположен на грани, противоположной грани с символом ■?
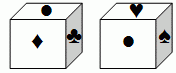
A) ● Б) ♦ В) ♥ Г) ♠ Д) ♣
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 35 - 1.25 = 33.75
|
Задание 24
|
На какое наибольшее количество групп можно распределить числа 1, 5, 8, 9, 10, 12 и 15, так, чтобы суммы чисел во всех группах были одинаковы? (В группе может быть и одно число. Каждое число входит только в одну группу.)
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|












 ?
?









