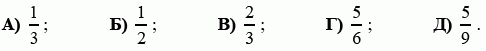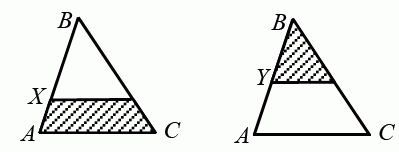"Кенгуру-2015"

19 марта 2015
Задание для 9-10 классов

Участник: Шутько Вадим, Деревнянская СШ, Столбцовский РООСиТ

На старте каждый участник получает 30 баллов

Задание 1

К какому из следующих чисел ближе всего произведение 20,15 · 51,02 ?

A) 100       Б) 1000       В) 10000       Г) 100000       Д) 1000000

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 30 + 3 = 33

Задание 2

Мама постирала носки и футболки, всего 29 штук, и попросила детей развесить их на верёвке так, чтобы между любыми двумя футболками висел ровно один носок. Дети выполнили это поручение. Сколько футболок находится на верёвке?

A) 10       Б) 11       В) 13       Г) 14       Д) 15

Правильный ответ: Д

Ответ участника: нет ответа

Промежуточный результат: 33

Задание 3

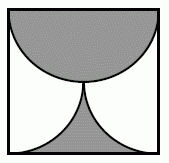
Найдите площадь серой части квадрата со стороной a. Здесь все дуги – дуги окружностей с центрами в серединах соответствующих сторон данного квадрата.

A) (πa²)/8

Б) a²/2

В) (πa²)/2

Г) a²/4

Д) (πa²)/4

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 33

Задание 4

Три сестры Аня, Вера и Света купили 30 конфет. Каждой досталось по 10 конфет. Но Аня заплатила 8 тыс. руб., Вера – 5 тыс. руб., а Света – 2 тыс. руб. На сколько больше конфет досталось бы Ане, если бы конфеты были поделены пропорционально внесённой плате?

A) 10       Б) 9       В) 8       Г) 7       Д) 6

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 33 + 3 = 36

Задание 5

Мистер Хайд хочет откопать клад, который он зарыл в своем саду много лет назад. Но он забыл его точное место расположения и лишь помнит, что зарыл клад не далее 5 м от старого дерева, но не ближе 5 м от каменной ограды. Какой из следующих рисунков наиболее точно показывает территорию, на которой находится клад?

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 36 - 0.75 = 35.25

Задание 6

Какой цифрой заканчивается значение выражения 2015⁰ + 2015¹ + 2015² + 2015⁵ ?

A) 1       Б) 5       В) 6       Г) 7       Д) 9

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 35.25 + 3 = 38.25

Задание 7

В классе 33 ученика. Когда их спросили о любимых предметах, то были названы математика и физкультура. Трое учеников назвали оба предмета. Число тех, кто назвал только математику, в 2 раза больше числа тех, кто назвал только физкультуру. Сколько всего учеников этого класса любят математику?

A) 15       Б) 18       В) 20       Г) 22       Д) 23

Правильный ответ: Д

Ответ участника: В

Промежуточный результат: 38.25 - 0.75 = 37.5

Задание 8

Какое из следующих чисел не является ни квадратом, ни кубом натурального числа?

A) 3¹⁰       Б) 5¹²       В) 4¹¹       Г) 6¹³       Д) 2⁹

Правильный ответ: Г

Ответ участника: нет ответа

Промежуточный результат: 37.5

Задание 9

Мистер Кэндл купил 100 свечей. Он сжигает одну свечу каждый день и делает одну новую свечу из остатка воска от семи сожжённых. Через сколько дней у него не останется ни одной свечи?

A) 112       Б) 114       В) 115       Г) 116       Д) 117

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 37.5 + 3 = 40.5

Задание 10

Число прямых углов в выпуклом пятиугольнике равно n. Укажите все возможные значения n.

A) 1, 2, 3

Б) 0, 1, 2, 3, 4

В) 0, 1, 2, 3

Г) 0, 1, 2

Д) 1, 2

Правильный ответ: В

Ответ участника: нет ответа

Промежуточный результат: 40.5

Задание 11

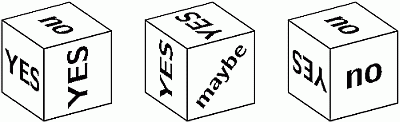
На рисунке показан вид одного и того же кубика с трёх разных позиций. Какова вероятность, что выпадет YES, если подбросить этот кубик?

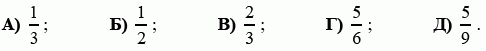
Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 40.5 - 1 = 39.5

Задание 12

Длина стороны каждой клетки на рисунке справа равна 1. Чему равна наименьшая длина пути по сторонам и диагоналям клеток от точки S до точки F?

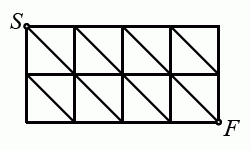
A) 2√5       Б) √10 + √2       В) 2 + 2√2       Г) 4√2       Д) 6

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 39.5 + 4 = 43.5

Задание 13

У каждого марсианина не менее двух ушей. Однажды встретились марсиане Имми, Димми и Тримми и посмотрели друг на друга. Имми сказал: «Я вижу 8 ушей». Димми сказал: «Я вижу 7 ушей». Тримми сказал: «А я вижу только пять ушей». Ни один марсианин не может видеть собственных ушей. Сколько ушей у Тримми?

A) 2       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 43.5 + 4 = 47.5

Задание 14

Сосуд в форме прямой призмы, основание которой – квадрат со стороной 10 см, заполнен водой до высоты h см. Твёрдый куб со стороной 2 см поставлен на дно призмы. При каком наименьшем значении h куб будет полностью погружён в воду?

A) 1,92 см       Б) 1,93 см       В) 1,94 см       Г) 1,91 см       Д) 1,90 см

Правильный ответ: А

Ответ участника: нет ответа

Промежуточный результат: 47.5

Задание 15

Площадь квадрата ABCD равна 80. На его сторонах отмечены точки E, F, G, и H (см. рис.), такие, что

AE = BF = CG = DH = 3 · HA

Чему равна площадь серой части данного квадрата?

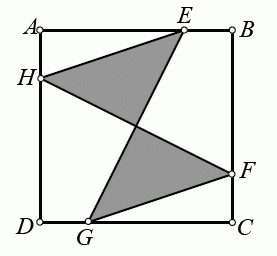
A) 20       Б) 25       В) 30       Г) 35       Д) 40

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 47.5

Задание 16

Произведение возрастов (целые числа) отца и сына равно 2015. Чему может быть равна разность их возрастов?

A) 26       Б) 29       В) 30       Г) 34       Д) 36

Правильный ответ: Г

Ответ участника: нет ответа

Промежуточный результат: 47.5

Задание 17

Четыре груза a, b, c и d лежали на чашах весов, которые не были уравновешены (см. рис.). После того, как два груза поменяли местами, положение чаш изменилось так, как показано на рисунке. Какие грузы поменяли местами?

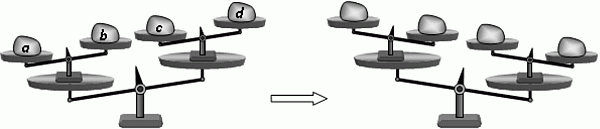
A) a и b

Б) b и d

В) b и c

Г) a и d

Д) a и c

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 47.5 + 4 = 51.5

Задание 18

Известно, что корни квадратного уравнения

x² - 85x + c = 0

являются простыми числами. Чему равна сумма цифр числа c?

A) 12       Б) 13       В) 14       Г) 15       Д) 21

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 19

Сколько существует трёхзначных чисел, у которых любые две соседние цифры отличаются на 3?

A) 12       Б) 14       В) 16       Г) 20       Д) 27

Правильный ответ: Г

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 20

Какое из следующих чисел является контрпримером к утверждению: если n – простое число, тогда ровно одно из чисел n - 2 и n + 2 является простым?

A) n = 11       Б) n = 19       В) n = 21       Г) n = 29       Д) n = 37

Правильный ответ: Д

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 21

Три круга определяют семь ограниченных областей на плоскости (см. рис.). В каждую из них нужно вписать число так, чтобы каждое из этих чисел равнялось сумме всех чисел в соседних областях. (Две области считаются соседними, если их границы имеют более одной общей точки.) Два числа уже вписаны, как показано на рисунке. Какое число должно быть вписано в центральной области?

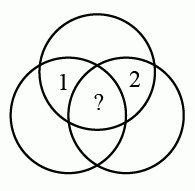
A) 0       Б) -3       В) 3       Г) -6       Д) 6

Правильный ответ: А

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 22

Пéтра имеет два различных словаря и три различных учебника. Сколько существует способов расставить их на полке в ряд так, чтобы все учебники стояли друг за другом и словари стояли друг за другом?

A) 12       Б) 24       В) 30       Г) 60       Д) 120

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 23

Сколько существует двузначных чисел, которые можно представить в виде суммы ровно шести различных степеней числа 2, включая 2⁰?

A) 0       Б) 1       В) 2       Г) 3       Д) 4

Правильный ответ: В

Ответ участника: нет ответа

Промежуточный результат: 51.5

Задание 24

В треугольнике ABC провели отрезки параллельно стороне AC: один раз через точку Х, а другой раз через точку Y (см рис.). Оказалось, что площади заштрихованных фигур равны. Чему равно отношение BY : YA, если BX : XA = 4 : 1 ?

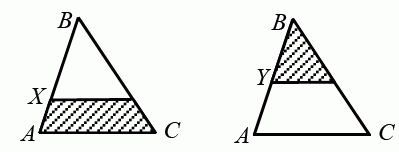
A) 1 : 1       Б) 2 : 1       В) 3 : 1       Г) 3 : 2       Д) 4 : 3

Правильный ответ: Г

Ответ участника: А

Промежуточный результат: 51.5 - 1.25 = 50.25

Задание 25

В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки 1 и 2. Какова длина биссектрисы?

A) √2       Б) √3       В) √4       Г) √5       Д) √6

Правильный ответ: В

Ответ участника: нет ответа

Промежуточный результат: 50.25

Задание 26

Сколько существует способов выбрать различные цифры a, b, c, так чтобы для следующих двузначных чисел выполнялись неравенства ab < bc < ca ?

A) 84       Б) 96       В) 125       Г) 201       Д) 402

Правильный ответ: А

Ответ участника: нет ответа

Промежуточный результат: 50.25

Задание 27

Когда одно из чисел 1, 2, 3, …, n вычеркнули, среднее арифметическое оставшихся чисел стало равно 4,75. Какое число вычеркнули?

A) 6       Б) 7       В) 8       Г) 9       Д) невозможно определить

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 50.25

Задание 28

Муравей ползает по рёбрам куба со стороной 1. Чему равна длина его кратчайшего пути, который начинается и заканчивается в одной вершине и проходит по всем рёбрам этого куба?

A) 12       Б) 14       В) 15       Г) 16       Д) 18

Правильный ответ: Г

Ответ участника: нет ответа

Промежуточный результат: 50.25

Задание 29

На доске записано десять различных чисел. Каждое из этих чисел, равное произведению остальных девяти чисел, подчёркнуто. Какое наибольшее количество чисел может быть подчёркнуто?

A) 1       Б) 2       В) 3       Г) 9       Д) 10

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 50.25

Задание 30

На прямой отмечено несколько точек. Рассмотрим все возможные отрезки с концами в отмеченных точках. Одна из отмеченных точек находится внутри 80 из этих отрезков, а другая – внутри 90 отрезков. Сколько точек отмечено на прямой?

A) 20       Б) 22       В) 28       Г) 32       Д) невозможно определить

Правильный ответ: Б

Ответ участника: нет ответа

Промежуточный результат: 50.25

Окончательный результат: 50.25

Место в Беларуси: 2678

Место в области: 485

Место в районе: 16

Место в школе: 2

Участник получает свидетельство и "приз для всех".