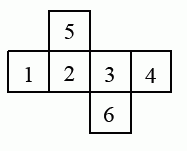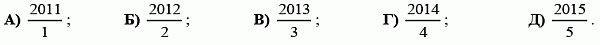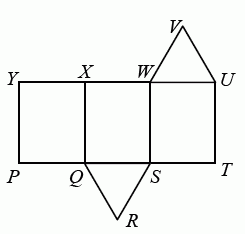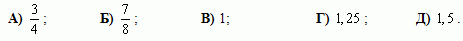Задание 1
|
На зонтике сверху написано слово KANGAROO:
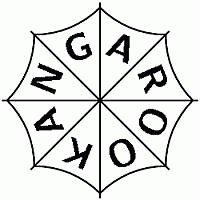
На каком из следующих рисунков изображён вид зонтика сбоку?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Из четырёх одинаковых прямоугольников сложили прямоугольник так, как показано на рисунке. Чему равна бо́льшая сторона полученного прямоугольника, если его меньшая сторона равна 10 см?

A) 10 см Б) 20 см В) 30 см Г) 40 см Д) 50 см
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Задание 3
|
К какому из следующих чисел ближе всего произведение 2,015 · 510,2 ?
A) 0,1 Б) 1 В) 10 Г) 100 Д) 1000
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Задание 4
|
На рисунке изображена развёртка поверхности куба. Саша подсчитал суммы чисел на противоположных гранях. Какие результаты у него получились?
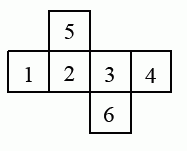
A) 4, 6, 11
Б) 4, 5, 12
В) 5, 6, 10
Г) 5, 7, 9
Д) 5, 8, 8
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Задание 5
|
Какое из следующих чисел не является целым?
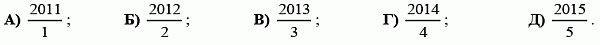
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Задание 6
|
Поезд от Кошице до Попрада через Прешов идёт 2 часа 10 минут. На часть пути от Кошице до Прешова уходит 35 мин. Сколько длится поездка на этом поезде от Прешова до Попрада?
A) 1 ч 35 мин
Б) 1 ч 45 мин
В) 1 ч 55 мин
Г) 2 ч 45 мин
Д) 1 ч 5 мин
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 41.25
|
Задание 7
|
На рисунке показана развёртка поверхности треугольной призмы. С каким отрезком совпадёт отрезок VU, если эту развертку снова свернуть в поверхность призмы?
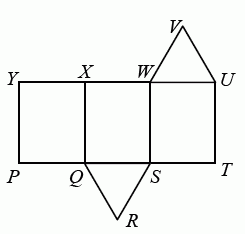
A) WV Б) XW В) XY Г) QR Д) RS
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Задание 8
|
Равносторонний треугольник имеет такой же периметр, как треугольник со сторонами 6, 10, 11. Чему равна сторона данного равностороннего треугольника?
A) 18 Б) 11 В) 10 Г) 9 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Задание 9
|
Когда белка спускается с дерева на землю, она никогда не удаляется от ствола дерева более, чем на 5 м. Кроме того, она боится подходить к конуре собаки ближе, чем на 5 метров. Какая из следующих картинок наиболее точно показывает территорию на земле, на которой может оказаться белка?

|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 43.5 - 0.75 = 42.75
|
Задание 10
|
Велосипедист едет со скоростью 5 м в секунду. Колёса его велосипеда имеют окружность длиной 125 см. Сколько полных оборотов делает каждое колесо за 5 секунд?
A) 4 Б) 5 В) 10 Г) 20 Д) 25
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 42.75 - 0.75 = 42
|
Задание 11
|
В классе никакие два мальчика не родились в один и тот же день недели, и никакие две девочки не родились в одном и том же месяце. Какое-то из этих условий нарушится, если в класс придёт ещё одна девочка или один мальчик. Сколько всего детей в этом классе?
A) 18 Б) 19 В) 20 Г) 24 Д) 25
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 42
|
Задание 12
|
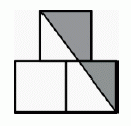
Фигура на рисунке состоит из трёх квадратов со стороной 1 и имеет вертикальную ось симметрии. Чему равна площадь серой части этой фигуры?
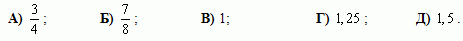
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 42
|
Задание 13
|
В равенстве
2 * 0 * 1 * 5 * 2 * 0 * 1 * 5 * 2 * 0 * 1 * 5 = 0
нужно заменить каждую звёздочку знаком “+” или “–” так, чтобы равенство стало верным. Какое наименьшее число знаков “+” может в нём оказаться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 42 - 1 = 41
|
Задание 14
|
В течение ливня выпало 15 литров осадков на 1 м2. На сколько поднялся уровень воды в открытом бассейне?
A) 150 см
Б) 0,15 см
В) 15 см
Г) 1,5 см
Д) зависит от размеров бассейна
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 41
|
Задание 15
|
У растения имеется 10 веток. На каждой ветке растёт либо 5 листочков, либо 2 листочка и 1 цветок. Какое из следующих чисел может быть числом всех листочков у этого растения?
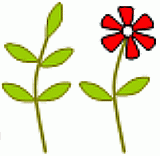
A) 45
Б) 39
В) 37
Г) 31
Д) ни одно из указанных в А) – Г)
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 41 - 1 = 40
|
Задание 16
|
Средняя оценка, которую получили школьники при тестировании, равна 6. Ровно 60% участников тестирования сдали тест. Средняя оценка школьников, которые сдали тест, равна 8. Чему равна средняя оценка школьников, которые не сдали тест?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 40 - 1 = 39
|
Задание 17
|
Бумажный квадрат согнули так, что одна его вершина совместилась с центром и получился пятиугольник (см. рис.). Известно, что площади пятиугольника и квадрата – последовательные целые числа. Какова площадь квадрата?

A) 2 Б) 4 В) 8 Г) 16 Д) 32
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 39 - 1 = 38
|
Задание 18
|
Миша сложил длины каких-то трёх сторон прямоугольника и получил 44 см. Катя тоже сложила длины каких-то трёх сторон этого же прямоугольника и получила 40 см. Чему равен периметр этого прямоугольника?
A) 42 см Б) 56 см В) 64 см Г) 72 см Д) 84 см
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 38 - 1 = 37
|
Задание 19
|
Каждый из 13 отрезков на рисунке справа нужно окрасить в синий, зелёный или красный цвет так, чтобы у каждого треугольника все стороны были разного цвета. Три из отрезков уже окрашены так, как показано на рисунке. В какой цвет должен быть окрашен отрезок x?
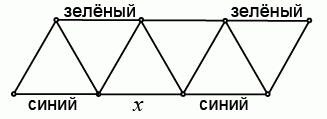
A) только в зелёный
Б) только в красный
В) только в синий
Г) в красный или синий
Д) так окрасить нельзя
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 37 - 1 = 36
|
Задание 20
|
Учительница спросила у пяти своих учеников, сколько из них сделали домашнее задание. Полина сказала, что никто не сделал, Берта сказала, что сделал только один ученик, Аня – что ровно два, Женя – что ровно три, а Игорь – что ровно четыре. Учительница знает, что те из детей, кто сделал домашнее задание, говорят правду, а те, кто не сделал – врут. Сколько из этих пяти школьников сделали домашнее задание?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 36 - 1 = 35
|
Задание 21
|
Рита хочет вписать по одному числу в каждую из семи ограниченных областей на рисунке так, чтобы каждое число равнялось сумме чисел в соседних областях. (Две области считаются соседними, если они имеют общий участок границы: дугу или отрезок). Два числа Рита уже вписала так, как показано на рисунке. Какое число она должна вписать в центральную область?
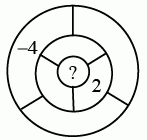
A) 1 Б) -2 В) 6 Г) -4 Д) 0
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 35 - 1.25 = 33.75
|
Задание 22
|
Пять целых чисел (не обязательно различных) записаны на пяти карточках. Петя вычислил суммы чисел на всех возможных парах карточек, но получил только три различных результата: 57, 70 и 83. Какое наибольшее число записано на этих карточках?
A) 35 Б) 42 В) 48 Г) 53 Д) 82
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
Задание 23
|
Квадрат площадью 30 см2 разбит на треугольники так, как показано на рисунке. Площади некоторых из этих треугольников указаны на рисунке. Какая из частей его диагонали самая длинная?
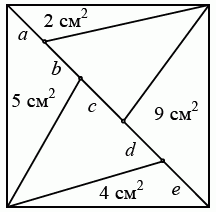
A) a Б) b В) c Г) d Д) e
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.5
|
Задание 24
|
В группе кенгуру вес трёх самых тяжёлых кенгуру составляет 60% от веса всей группы, а двух самых лёгких – 25% от веса группы. Сколько кенгуру в данной группе?
A) 6 Б) 7 В) 8 Г) 10 Д) 12
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.5
|
Задание 25
|
У Кирилла есть семь кусков проволоки длиной 1 см, 2 см, 3 см, 4 см, 5 см, 6 см и 7 см. Какое наименьшее количество из этих кусков ему понадобится, чтобы спаять каркас куба со стороной 1 см без перекрытий? Куски нужно использовать целиком, можно сгибать, но нельзя ломать.
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.5
|
Задание 26
|
В трапеции PQRS (PQ || SR): ∠RSP = 120°, PQ = 3 · RS = 3 · SP. Найдите ∠PQR.
A) 15° Б) 22,5° В) 25° Г) 30° Д) 45°
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.5
|
Задание 27
|
На прямой отмечено 5 точек. Саша вычислил расстояния между всеми возможными парами этих точек. Он получил (в порядке возрастания) следующие результаты: 2, 5, 6, 8, 9, x, 15, 17, 20 и 22. Чему равно x?
A) 10 Б) 11 В) 12 Г) 13 Д) 14
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.5
|
Задание 28
|
Вчера Вася записал семизначный номер телефона своего друга Эдика. Но одну из цифр при записи он пропустил. Вася не знает, какая это цифра и в какой позиции она расположена. Какое наименьшее число различных 7-значных номеров ему нужно испытать, чтобы наверняка дозвониться до Эдика? (Номер телефона может начинаться с любой цифры, включая 0.)
A) 55 Б) 60 В) 64 Г) 70 Д) 80
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 32.5 - 1.25 = 31.25
|
Задание 29
|
Мария делит с остатком число 2015 последовательно на 1, на 2, на 3 и т.д. до 1000 включительно. Какой наибольший остаток у неё получится?
A) 5 Б) 215 В) 671 Г) 1007 Д) другое значение
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 31.25 - 1.25 = 30
|
Задание 30
|
Каждое натуральное число нужно окрасить в зелёный или красный цвет согласно следующим двум правилам:
1) сумма любых двух различных красных чисел есть красное число;
2) сумма любых двух различных зелёных чисел есть зелёное число.
Сколько различных способов такой окраски существует?
(Две окраски чисел считаются различными, если найдётся число, окрашенное в них в различные цвета. В окраске не обязательно должны быть числа разных цветов.)
A) 0 Б) 2 В) 4 Г) 6 Д) более 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 5 = 35
|