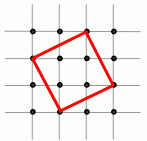
Задание 1
|
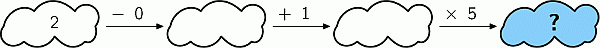
A) 6 Б) 7 В) 8 Г) 10 Д) 15
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 24 + 3 = 27
|
Задание 2
|
У Эрика есть 10 одинаковых металлических пластин.
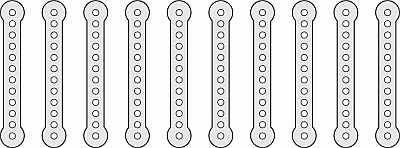
Он свинтил их парами в 5 более длинных пластин (см. рис.). Какая из них самая длинная?
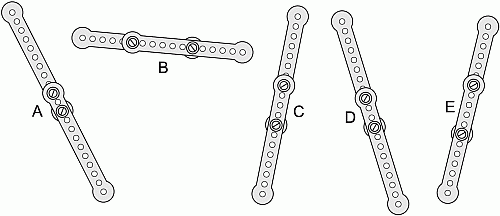
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 27 + 3 = 30
|
Задание 3
|
Какое число закрыто квадратом на втором из двух следующих правильных равенств, если известно, что треугольниками закрыты одинаковые числа?
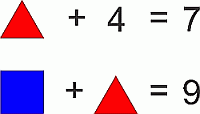
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Задание 4
|
Произведение цифр некоторого двузначного числа равно 15. Чему равна сумма цифр этого числа?
A) 2 Б) 4 В) 6 Г) 8 Д) 10
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33 + 3 = 36
|
Задание 5
|
Мы хотим соединить отрезками 9 точек на окружности. Начав c точки 1, будем проводить отрезки к каждой второй точке, пока не вернёмся в точку 1. Первые два отрезка уже нарисованы на рисунке.
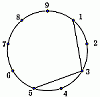
Какую фигуру мы получим, когда процесс будет закончен?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 36 + 3 = 39
|
Задание 6
|
У Люси в кошельке было несколько кенго (см. рис.).
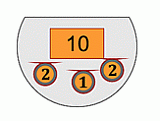
Она зашла в магазин и купила мячик за 7 кенго. Сколько кенго осталось в кошельке у Люси после покупки мячика?

|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Задание 7
|
На рисунке изображён остров с необычной береговой линией и несколькими лягушками. Сколько из этих лягушек сидит на острове?
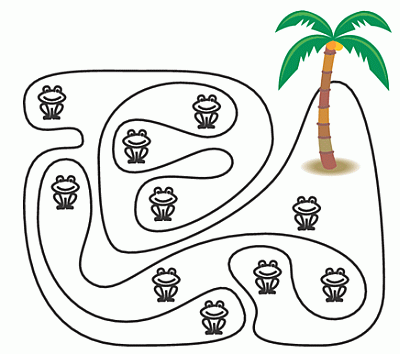
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
Задание 8
|
Сверху на зонтике написано слово KANGAROO (см. рис.).
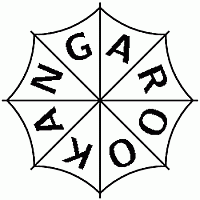
На каком из следующих рисунков изображён вид зонтика сбоку?

|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 37.5 - 0.75 = 36.75
|
Задание 9
|
Вася хочет разрезать бумажную фигуру на рисунке
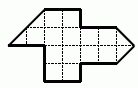
на треугольники вида  . Сколько треугольников у него получится?
. Сколько треугольников у него получится?
A) 8 Б) 12 В) 14 Г) 15 Д) 16
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 36.75 + 4 = 40.75
|
Задание 10
|
У Люси есть 7 яблок и 2 банана. Она дала 2 яблока Юре, который взамен дал ей несколько бананов. В результате у Люси яблок и бананов стало поровну. Сколько бананов дал Юра Люсе?
A) 2 Б) 3 В) 4 Г) 5 Д) 7
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 40.75 + 4 = 44.75
|
Задание 11
|
Толя сложил куб из серых и белых кубиков (см. рис.) так, что никакие два кубика одного цвета не соприкасаются по грани. Сколько белых кубиков Толя использовал?

A) 10 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 44.75 - 1 = 43.75
|
Задание 12
|
В конькобежных соревнованиях участвовало 10 спортсменов. Коля опередил на 3 гонщика больше, чем опередили его. Какое место занял Коля?
A) 1 Б) 3 В) 4 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 43.75 - 1 = 42.75
|
Задание 13
|
У Иосифа есть 4 игрушки: автомобиль, самолёт, мяч и корабль. Он хочет расставить их в ряд на полке так, чтобы рядом с автомобилем стояли корабль и самолёт. Сколько существует способов так расставить игрушки?
A) 2 Б) 4 В) 5 Г) 6 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 42.75 + 4 = 46.75
|
Задание 14
|
Петя едет на велосипеде по дорожкам в парке (см. рис.). Он стартует из пункта S в направлении стрелки. На первом перекрёстке Петя поворачивает направо, затем налево, потом снова направо, затем налево, и т. д. Какой из пунктов он не сможет проехать ни разу?
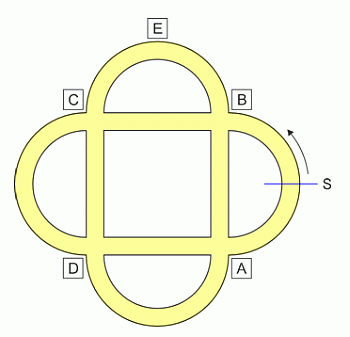
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 46.75 - 1 = 45.75
|
Задание 15
|

На рисунке – 5 божьих коровок. Две божьи коровки дружат между собой, если количества пятен у них на крыльях отличаются ровно на 1. В день проведения конкурса «Кенгуру» каждая из божьих коровок отправила одно приветственное SMS каждой своей подружке. Сколько поздравительных SMS было отправлено?
A) 2 Б) 4 В) 6 Г) 8 Д) 9
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 45.75 + 4 = 49.75
|
Задание 16
|

Фигуру на рисунке разрезали на 3 одинаковые части. Как может выглядеть одна такая часть?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 49.75 + 4 = 53.75
|
Задание 17
|
Лиза вырезала из бумаги фигуру (см. рис.) и хочет свернуть её так, чтобы получился куб. Но по ошибке одна клетка у этой фигуры оказалась лишняя. Какую клетку из этой фигуры нужно вырезать, чтобы фигура не распалась на части, и чтобы после этого её можно было бы свернуть в куб?
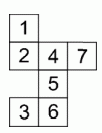
A) 1 Б) 2 В) 3 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 53.75
|
Задание 18
|
Имеются три квадратные пластины со светлыми прозрачными и чёрными непрозрачными клетками (см. рис.). Какое наибольшее число чёрных клеток можно будет увидеть, если наложить эти квадраты друг на друга так, чтобы их вершины совпали, и посмотреть на них сверху? (Квадраты можно поворачивать, но не переворачивать.)

A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 53.75
|
Задание 19
|
В пять клеток креста нужно вписать числа 2, 3, 5, 6 и 7 (каждое по одному разу) так, чтобы сумма трёх чисел в столбце равнялась сумме трёх чисел в строке. Какое число нужно вписать в центральную клетку?

A) только 3
Б) только 5
В) только 7
Г) 5 или 7
Д) 3, 5 или 7
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 53.75 - 1.25 = 52.5
|
Задание 20
|

У Пети есть десять шариков, пронумерованных числами от 0 до 9. Он раздал их трём своим друзьям: 3 шарика – Диме, 4 – Жене и 3 – Ане. После этого друзья Пети вычислили произведения чисел на полученных ими шариках. У Димы получилось 0, у Жени – 72, а у Ани – 90. Чему равна сумма чисел на шариках, которые получил Дима?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 52.5 + 5 = 57.5
|
Задание 21
|
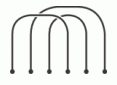
На рисунке показаны три верёвки. С какими из следующих трёх верёвок их нужно связать, совместив концы в том же порядке, как они изображены на рисунках, чтобы получилась одна замкнутая верёвка?

|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 57.5 - 1.25 = 56.25
|
Задание 22
|
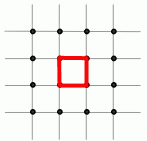
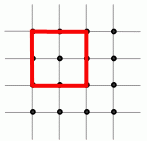
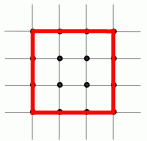
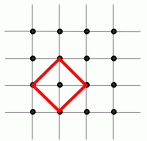
На клетчатой бумаге отмечено 16 точек так, как показано на рисунке. Сколько всего существует не равных квадратов с вершинами в отмеченных точках?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 56.25
|
Задание 23
|
Том нарисовал кабана, акулу и носорога и разрезал каждого из них на три части так, как показано на рисунке. Сколько различных (реальных и нереальных) животных можно получить, если из всех этих частей выбрать одну переднюю, одну среднюю и одну заднюю часть и склеить их соответствующим образом?

A) 3 Б) 9 В) 15 Г) 27 Д) 30
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 56.25 - 1.25 = 55
|
Задание 24
|
Аня, Берта, Чарли, Дэвид и Лиза пекли печенье в субботу и воскресенье. За два дня Аня испекла 24 печенья, Берта – 25, Чарли – 26, Дэвид – 27, а Лиза – 28. При этом, кто-то из них в течение двух дней испек в 2 раза больше печенья, чем в субботу, кто-то – в 3 раза больше, чем в субботу, кто-то – в 4 раза, кто-то – в 5 раз, а кто-то – в 6 раз. Кто из этих детей испёк больше всего печенья в субботу?
A) Аня Б) Берта В) Чарли Г) Дэвид Д) Лиза
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 55 + 5 = 60
|
По условию, кто-то из детей за два дня испек в 2 раза больше печений, чем в субботу. Следовательно, испеченное им число печений делится на 2. Далее, кто-то испек в 3 раза больше печений, чем в субботу, и, значит, испеченное им число печений делится на 3. Аналогично, еще у кого-то число испеченных печений делится на 4 раза, у кого-то – на 5 и у кого-то – на 6. Из условия известно, что Аня испекла 24 печенья, Берта – 25, Чарли – 26, Дэвид – 27, а Лиза – 28. Из этих чисел на 6 делится только число 24. Такое число печений за два дня испекла Аня. Тогда в субботу она испекла 24 : 6 = 4 печенья. На 5 делится только число 25. Такое число печений испекла за два дня Берта. Тогда в субботу она испекла 25 : 5 = 5 печений. Из оставшихся чисел на 4 делится только число 28. Такое число печений за два дня испекла Лиза. Тогда в субботу она испекла 28 : 4 = 7 печений. На 3 среди оставшихся чисел делится только число 27. Такое число печений за два дня испек Дэвид. Тогда в субботу он испек 27 : 3 = 9 печений. У нас остается Чарли, который испек за два дня 26 печений, что в 2 раза больше, чем в субботу. Следовательно, в субботу он испек 26 : 2 = 13 печений. Видим, что именно он, Чарли, испек в субботу больше всего печений.



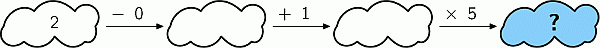


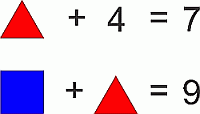








 . Сколько треугольников у него получится?
. Сколько треугольников у него получится?