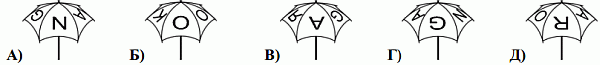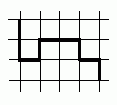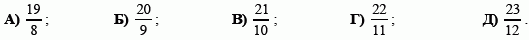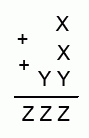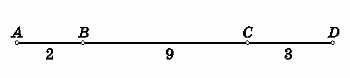Задание 1
|
У какой из следующих фигур ровно половина фигуры – серая?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Сверху на зонтике написано слово KANGAROO.
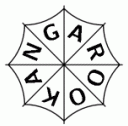
Какой из следующих рисунков не может быть видом зонтика сбоку?
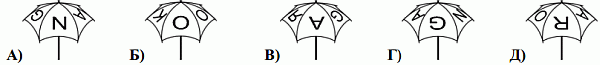
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 33 + 3 = 36
|
Задание 3
|
Серёжа окрасил 9 клеток квадрата в чёрный, белый и серый цвета так, как показано на рисунке. Какое наименьшее число клеток ему нужно перекрасить, чтобы никакие две соседние по стороне клетки не имели один и тот же цвет?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 36 - 0.75 = 35.25
|
Задание 4
|
В деревне у бабушки 10 куриц. Пять из них несут по одному яйцу в день, а другие пять – по одному яйцу через день. Сколько яиц снесут эти 10 куриц за 10 дней?
A) 75 Б) 60 В) 50 Г) 25 Д) 10
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Задание 5
|
На клетчатой бумаге нарисована чёрная линия (см. рис.). Найдите её длину, если известно, что площади клеток равны 4 см2.
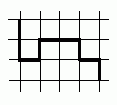
A) 16 см Б) 18 см В) 20 см Г) 21 см Д) 23 см
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Задание 6
|
Какая из следующих дробей меньше 2?
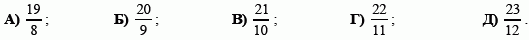
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 41.25 + 3 = 44.25
|
Задание 7
|
Сколько весит пеликан Дита (см. рис.)?
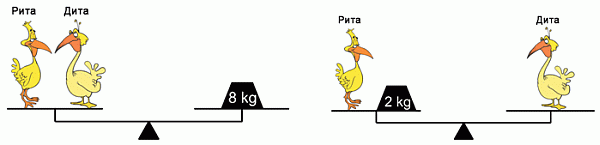
A) 2 кг Б) 3 кг В) 4 кг Г) 5 кг Д) 6 кг
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 44.25 - 0.75 = 43.5
|
Задание 8
|
Петя просматривает через лупу рисунок:

Какой из следующих фрагментов рисунка он не сможет увидеть?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Задание 9
|
На каждой ветке комнатного растения в кабинете биологии имеется либо 5 листочков, либо 2 листочка и 1 цветок (см рис.). Всего у растения 6 цветочков и 32 листочка. Сколько всего веток у этого растения?
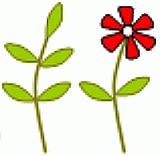
A) 10 Б) 12 В) 13 Г) 15 Д) 16
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 46.5 + 3 = 49.5
|
Задание 10
|
У Аллы есть 4 одинаковых бумажных полоски. Она склеила 2 из них с наложением 10 см и получила полоску длиной 50 см (см. рис.). Из двух оставшихся полосок Алла хочет склеить полоску длиной 56 см. Сколько см в этом случае должно составить наложение?

A) 4 см Б) 6 см В) 8 см Г) 10 см Д) 12 см
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 49.5 + 3 = 52.5
|
Задание 11
|
Толя нарисовал фигуру, состоящую из 6 квадратов со стороной 1 см (см. рис.). Какой периметр имеет эта фигура?
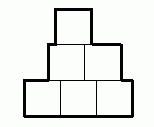
A) 9 см Б) 10 см В) 11 см Г) 12 см Д) 13 см
Примечание:
вопрос не оценивался из-за неправильного изображения к заданию в белорусском переводе.
|
Вопрос не оценивался
|
Ответ участника: Г
|
Промежуточный результат: 52.5
|
Задание 12
|
Каждый день Маша пишет дату и считает сумму записанных цифр. Например, 19 марта она записала 19.03 и вычислила:1+9+0+3=13. Какую наибольшую сумму она может получить в течение года?
A) 7 Б) 13 В) 14 Г) 16 Д) 20
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 52.5 + 4 = 56.5
|
Задание 13
|
Из четырёх одинаковых прямоугольников сложили прямоугольник так, как показано на рисунке. Чему равна бо́льшая сторона этих прямоугольников, если меньшая сторона равна 1 см?

A) 4 см Б) 3 см В) 2 см Г) 1 см Д) 0,5 см
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 56.5 + 4 = 60.5
|
Задание 14
|
Какая из этих пяти фигур не может быть развёрткой поверхности пирамиды?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 60.5 + 4 = 64.5
|
Задание 15
|
На одной стороне улицы расположены подряд 9 домов. В каждом доме живёт по крайне мере один человек. В любых двух соседних домах вместе живёт не более шести человек. Какое наибольшее число людей может жить во всех этих домах?
A) 23 Б) 25 В) 27 Г) 29 Д) 31
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 64.5 - 1 = 63.5
|
Задание 16
|
Люся и её мама обе родились в январе. Сегодня, 19 марта 2015 года, Люся сложила четыре числа: год своего рождения, год рождения мамы, свой возраст (в годах) и возраст её мамы. Какой результат у неё получился?
A) 4028 Б) 4029 В) 4030 Г) 4031 Д) 4032
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 63.5
|
Задание 17
|
Площадь прямоугольника равна 12 см2, длины сторон выражаются целыми числами сантиметров. Каким из следующих может быть периметр этого прямоугольника?
A) 20 см Б) 26 см В) 28 см Г) 32 см Д) 48 см
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 63.5 + 4 = 67.5
|
Задание 18
|
Каждый из девяти отрезков на рисунке нужно окрасить в синий, зелёный или красный цвет так, чтобы у каждого треугольника все стороны были разного цвета. Три из отрезков уже окрашены так, как показано на рисунке. В какой цвет должен быть окрашен отрезок x?
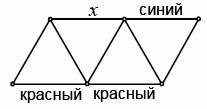
A) только в синий
Б) только в зелёный
В) только в красный
Г) в любой из трёх указанных
Д) так отрезки окрасить нельзя
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 67.5 + 4 = 71.5
|
Задание 19
|
В пакете лежат 3 зелёных яблока, 5 жёлтых яблок, 7 зелёных груш и 2 жёлтые груши. Саша, не глядя, вынимает фрукты из пакета один за другим. Какое наименьшее количество фруктов он должен вынуть, чтобы среди них наверняка оказались хотя бы одно яблоко и одна груша одинакового цвета?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 71.5 - 1 = 70.5
|
Задание 20
|
Новая шахматная фигура "кенгуру" за один ход прыгает либо на 3 клетки по вертикали и 1 по горизонтали, либо на 3 клетки по горизонтали и 1 по вертикали (см. рис.). За какое наименьшее число ходов кенгуру может попасть с клетки, на которой он изображён, на клетку A?
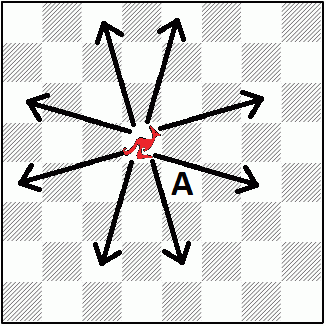
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 70.5 + 4 = 74.5
|
Задание 21
|
В примере на сложение (см. рис.), разные цифры заменили разными буквами, одинаковые цифры – одинаковыми буквами. Какую цифру заменили буквой Х?
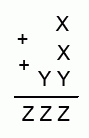
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 74.5 + 5 = 79.5
|
Задание 22
|
Джейн купила 3 игрушки. За первую она заплатила половину её денег и ещё 1$, за вторую – половину оставшихся денег и ещё 2$, наконец, за третью – половину оставшихся денег и ещё 3$. В результате все деньги у неё закончились. Сколько денег было у Джейн первоначально?
A) 36$ Б) 45$ В) 34$ Г) 65$ Д) 100$
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 79.5 - 1.25 = 78.25
|
Задание 23
|
Лиза вырезала из бумаги фигуру на рисунке и хочет свернуть её так, чтобы получился куб. Но по ошибке одна клетка у этой фигуры оказалась лишняя. Какую клетку из этой фигуры нужно вырезать, чтобы она не распалась на части, и чтобы после этого её можно было бы свернуть в куб?
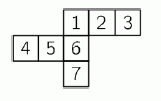
A) только 4
Б) только 7
В) только 3 или 4
Г) только 3 или 7
Д) только 3, 4 или 7
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 78.25 + 5 = 83.25
|
Задание 24
|
Число 100 умножили то ли на 2, то ли на 3. Затем результат увеличили то ли на 1, то ли на 2. Наконец, новый результат разделили то ли на 3, то ли на 4. Что получилось в итоге, если известно, что это целое число?
A) 50
Б) 51
В) 67
Г) 68
Д) возможно несколько целых результатов
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 83.25 + 5 = 88.25
|
Задание 25
|
Какое наибольшее значение может принимать разность двузначных чисел BD - AC, где буквы обозначают цифры, такие, что A<B<C<D?
A) 86 Б) 61 В) 56 Г) 50 Д) 16
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 88.25
|
Задание 26
|
Маша записала по одному числу на каждой грани куба. Затем для каждой вершины она вычислила сумму чисел на всех трёх гранях, которым принадлежит данная вершина. Для вершин C, D и E эти суммы оказались равны 14, 16 и 24, соответственно. Чему равна сумма для вершины F?
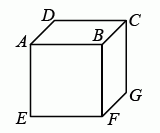
A) 15 Б) 19 В) 22 Г) 24 Д) 26
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 88.25 - 1.25 = 87
|
Задание 27
|
Поезд состоит из 12 вагонов. В каждом вагоне одинаковое число купе. Миша едет в 3-ем вагоне, 18-ом купе от локомотива, а Женя – в 7-ом вагоне, 50-ом купе от локомотива. Сколько купе в каждом вагоне?
A) 7 Б) 8 В) 9 Г) 10 Д) 12
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 87 + 5 = 92
|
Задание 28
|
Сколько существует способов поместить трёх кенгуру в 3 из 7 клеток так, чтобы никакие два кенгуру не оказались в соседних клетках?

A) 7 Б) 8 В) 9 Г) 10 Д) 11
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 92 - 1.25 = 90.75
|
Задание 29
|
На прямой отмечено 4 точки. Вася вычислил расстояния между всеми парами этих точек и расположил результаты в порядке возрастания: 2, 3, x, 11, 12 и 14. Чему равно x?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 90.75
Пусть отмеченные точки – это точки (слева направо) A, B, C и D. Ясно, что наибольшее из расстояний – 14 – есть расстояние между крайними точками A и D. Точки B и C на отрезке AD делят его на три отрезка. Среди них есть отрезок длины 2 и отрезок длины 3. Действительно, поскольку 2 и 3 – два наименьших расстояния между отмеченными точками, то между соответствующими этим расстояниям отмеченными точками не может быть других отмеченных точек. В противном случае два наименьших расстояния были бы меньше 2 и 3. Тогда длина третьего из отрезков, на которые делят отрезок AD точки B и C, равна 14 – 2 – 3 = 9. Это и есть искомое значение x, поскольку оно отсутствует среди чисел, указанных в условии задачи. Одно из двух возможных расположений точек показано на следующем рисунке.
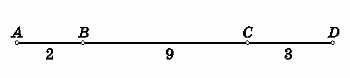
Точки также будут удовлетворять условию задачи, если AB = 3, CD = 2.
|
Задание 30
|
Вася сложил из кубиков со стороной 1 большой куб со стороной 4. Затем он окрасил 3 грани этого куба в красный цвет, а 3 другие грани – в синий цвет. При этом ни у одного маленького кубика не оказалось трёх граней, окрашенных в красный цвет. Сколько маленьких кубиков имеют и красную грань, и синюю грань?
A) 0 Б) 8 В) 12 Г) 24 Д) 32
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 90.75
Выясним, как выглядит окраска куба, удовлетворяющая условию задачи. Куб всегда можно повернуть так, чтобы передняя грань была красной. Поэтому считаем, что передняя грань – красная. Имеются еще две красные грани. Только одна из них может быть задней. Поэтому у передней грани есть по крайней мере одна соседняя красная грань. Пусть для определенности это правая грань. Тогда третьей красной гранью не может быть ни верхняя, ни нижняя, иначе на каком-то конце ребра между передней и правой гранями будет кубик с тремя красными гранями, что противоречит условию. Следовательно, третья красная грань – это левая грань или задняя грань. Для определенности можно считать, что это задняя грань. Таким образом, с точностью до поворотов и симметрий окраску, удовлетворяющую условию задачи, можно считать единственной. Она показана на рисунке 1, где жирной линией изображены ребра между гранями разного цвета. Только вдоль этих ребер находятся те кубики, которые имеют грани разного цвета. Эти кубики показаны на рисунке 2. Легко подсчитать, что их количество равно 24.
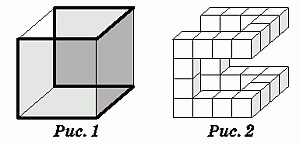
|