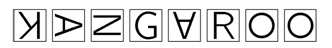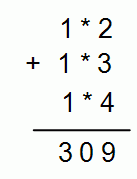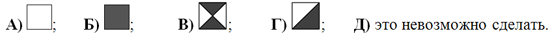Задание 1
|
Аня сложила из карточек с буквами слово KANGAROO. К сожалению, некоторые буквы оказались повёрнутыми:
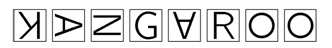
За два поворота, как показано на рисунке, Аня может правильно расположить первую букву (K), за один поворот – вторую букву (A). Какое наименьшее число таких поворотов нужно сделать, чтобы все буквы расположить правильно?
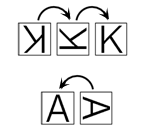
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Торт весит 900 граммов. Его разрезали на 4 куска. Сколько весит наибольший кусок, если известно, что он весит столько же, сколько весят остальные 3 куска вместе?
A) 250 г Б) 300 г В) 400 г Г) 450 г Д) 500 г
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33 + 3 = 36
|
Задание 3
|
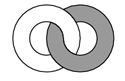
Два кольца, белое и серое, соединены так, как показано на рисунке. Как будут выглядеть эти кольца, если посмотреть на них с обратной стороны?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 36 + 3 = 39
|
Задание 4
|
В следующем примере на сложение некоторые цифры заменили звёздочками. Чему равна сумма этих цифр?
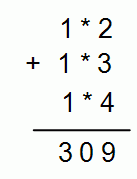
A) 0 Б) 1 В) 2 Г) 3 Д) 10
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Задание 5
|
Чему равна разность между наименьшим пятизначным числом и наибольшим четырёхзначным числом?
A) 1 Б) 10 В) 1111 Г) 9000 Д) 9900
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Задание 6
|
Найдите периметр прямоугольника, если известно, что его сложили из двух частей квадрата площади 144 см2, разрезанного пополам.
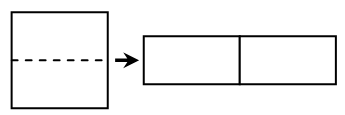
A) 24 см Б) 30 см В) 48 см Г) 60 см Д) 72 см
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Задание 7
|
Катя сложила из 38 спичек квадрат и треугольник. Каждая сторона треугольника состоит из 6 спичек. Сколько спичек составляют сторону квадрата?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Задание 8
|
Ожерелье на рисунке состоит из черных и белых жемчужин. Аня хочет снять с него
5 черных жемчужин, снимая по одной жемчужине – каждый раз с любого из концов ожерелья. Какое наименьшее число белых жемчужин ей придётся при этом снять?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Задание 9
|
Гарри Потер участвовал в гонке верхом на метле. Дистанция состоит из 5 кругов. Время, когда Гарри стартовал, и время, когда он заканчивал круги, указаны в таблице. Какой круг занял наименьшее время?
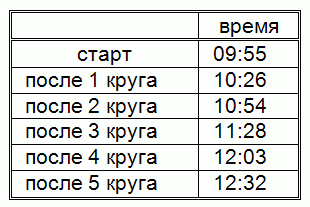
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 46.5 + 3 = 49.5
|
Задание 10
|
Цифровые часы Бена имеют дефект. Три горизонтальных линии в крайней правой цифре не работают. Бен посмотрел на часы, и в то же мгновение их показания изменились так, как показано на рисунке. В какое время это случилось?

A) 12:40 Б) 12:42 В) 12:44 Г) 12:47 Д) 12:49
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 49.5 + 3 = 52.5
|
Задание 11
|
Какую плитку нужно добавить к восьми плиткам на рисунке, чтобы площадь белой части полученного квадрата стала равна площади его черной части?
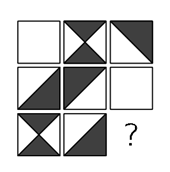
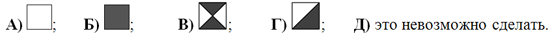
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 52.5 - 1 = 51.5
|
Задание 12
|
Гена и Женя стартовали из одной и той же точки. Гена прошёл 1 км на север, 2 км на запад, 4 км на юг и, наконец, 1 км на запад. А Женя прошёл 1 км на восток, затем 4 км на юг и 4 км на запад. Как ему следует ещё пройти, чтобы встретиться с Геной?
A) он уже встретился
Б) 1 км на север
В) 1 км на северо-запад
Г) более 1 км на северо-запад
Д) 1 км на запад
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 51.5 - 1 = 50.5
|
Задание 13
|
В летнем лагере 7 школьников едят мороженое каждый день, 9 – через день, а остальные мороженого вообще не едят. Вчера 13 школьников ели мороженое. Сколько школьников будут есть мороженое сегодня?
A) 7 Б) 8 В) 9 Г) 10 Д) невозможно определить
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 50.5 - 1 = 49.5
|
Задание 14
|
Кенгуру A, Б, В, Г и Д сидят в указанном порядке (по ходу часовой стрелки) за круглым столом. Как только прозвенел звонок, каждый кенгуру, кроме одного, поменялcя местом с одним из соседей. В результате они стали сидеть в следующем порядке (по ходу часовой стрелки): А, Д, Б, Г, В. Какой из кенгуру остался на месте?
A) А Б) Б В) В Г) Г Д) Д
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 49.5 - 1 = 48.5
|
Задание 15
|
Из четырёх фигур в вариантах ответа можно сложить квадрат. Какая фигура лишняя?

|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 48.5 - 1 = 47.5
|
Задание 16
|
Произведение трёх цифр равно 135. Чему равна их сумма?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 47.5 + 4 = 51.5
|
Задание 17
|
В ресторане есть 16 столов, к каждому приставлено 3, 4 или 6 стульев. Всего за столы с 3 и 4 стульями можно посадить 36 посетителей, а за всеми столами можно посадить 72 посетителя. Сколько в ресторане столов с 3 стульями?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 51.5
|
Задание 18
|
Точки A, B, C, D, E, F расположены на одной прямой в указанном порядке. Известно, что AF=35, AC=12, BD=11, CE=12 и DF=16. Найдите BE.
A) 13 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 51.5 + 4 = 55.5
|
Задание 19
|
Лариса раскладывает на столе конфеты на равные по количеству конфет кучки. Сначала она попробовала разложить их на 3 кучки, но 2 конфеты у неё остались лишними. Тогда она попробовала разложить все конфеты на 5 кучек, и снова у неё 2 конфеты остались. Какое наименьшее количество конфет Ларисе нужно ещё добавить, чтобы она смогла разложить все конфеты и на 3 кучки, и на 5 кучек и чтобы ни одной конфеты не осталось?
A) 1 Б) 3 В) 4 Г) 10 Д) 13
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 55.5 + 4 = 59.5
|
Задание 20
|
Грани куба пронумерованы числами 1, 2, 3, 4, 5 и 6. Грани 1 и 6 имеют общее ребро. Общие ребра также у граней 1 и 5, 1 и 2, 6 и 5, 6 и 4, 6 и 2. Какое число находится на грани, противоположной грани с числом 4?
A) 1 Б) 2 В) 3 Г) 5 Д) невозможно определить
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 59.5
|
Задание 21
|
Куб 3×3×3 состоит из 27 единичных кубиков. Какое наименьшее число кубиков нужно убрать, чтобы полученная фигура имела одинаковый вид сверху, спереди и справа – такой, как показано на рисунке?
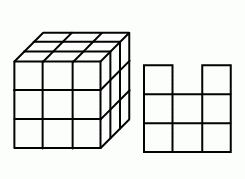
A) 4 Б) 5 В) 6 Г) 7 Д) 9
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 59.5
|
Задание 22
|
У Пети на карманном проигрывателе записано 5 песен: А, Б, В, Г и Д, которые исполняются в указанном порядке по кругу без пауз. Песня A длится 3 минуты, песня Б – 2 минуты 30 секунд, песня В – 2 минуты, песня Г – 1 минуту 30 секунд, и песня Д – 4 минуты. Когда Петя вышел из дома, звучала песня В. Какая песня звучала ровно через 1 час, когда Петя вернулся домой?
A) А Б) Б В) В Г) Г Д) Д
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 59.5 + 5 = 64.5
|
Задание 23
|
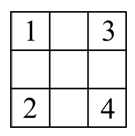
Дима вписал каждое из чисел от 1 до 9 в клетки таблицы 3×3. На рисунке можно видеть только четыре из вписанных чисел. Дима подсчитал, что для числа 5 сумма чисел в соседних по стороне клетках равна 9. Чему равна сумма чисел в соседних по стороне клетках у числа 6?
A) 14 Б) 15 В) 17 Г) 28 Д) 29
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 64.5
|
Задание 24
|
Вдоль одной стороны парковой аллеи растёт 60 деревьев. Каждое второе дерево – клён, каждое третье дерево – либо липа, либо клён. Остальные деревья – берёзы. Сколько берёз растёт вдоль аллеи?
A) 10 Б) 15 В) 20 Г) 24 Д) 30
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 64.5 - 1.25 = 63.25
|
Задание 25
|
На поверхности прозрачного куба нарисована синяя линия (см. рис.). Какой вид (из указанных в вариантах ответа) не может иметь этот куб ни с одной стороны?
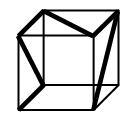

|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 63.25 - 1.25 = 62
|
Задание 26
|
Король и его посыльные едут из зáмка в летнюю резиденцию со скоростью 5 км/ч. Каждый час король направляет посыльного со скоростью 10 км/ч назад в зáмок. Через какие интервалы времени посыльные прибывают друг за другом в зáмок?
A) 30 мин Б) 60 мин В) 75 мин Г) 90 мин Д) 120 мин
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 62 - 1.25 = 60.75
|
Задание 27
|
На доске записаны три цифры (не обязательно различные). Алла сложила их и получила сумму 15. Затем она стёрла одну из цифр, вместо неё записала цифру 3 и вычислила произведение этих трёх цифр. Оно оказалось равным 36. Какой могла быть цифра, которую Алла стёрла?
A) либо 6, либо 7
Б) либо 7, либо 8
В) только 6
Г) только 7
Д) только 8
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 60.75 - 1.25 = 59.5
|
Задание 28
|
Кролик Вася любит капусту и морковь. Каждый день он съедает либо 9 морковок, либо 2 кочана капусты, либо 1 кочан капусты и 4 морковки. Но в некоторые дни он голодает и ест только траву. За прошлые 10 дней Вася съел в общей сложности 30 морковок и 9 кочанов капусты. Сколько из этих 10 дней кролик голодал?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 59.5 - 1.25 = 58.25
|
Задание 29
|
В стране Дождьляндии каждому солнечному дню непременно предшествуют два последовательных дождливых дня. Кроме того, спустя пять дней после каждого дождливого дня также следует дождливый день. Сегодня солнечный день. На какое наибольшее число дней вперёд можно с уверенностью предсказать погоду в этой стране?
A) на один
Б) на два
В) на четыре
Г) ни на один
Д) на любое число дней
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 58.25 - 1.25 = 57
|
Задание 30
|
У бабушки 10 внуков, и все они имеют различные возрасты. Алексей – самый старший из них. Однажды бабушка подсчитала, что сумма возрастов всех её внуков равна 180 (все возрасты – целые числа). Какой наименьший возраст может быть у Алексея?
A) 19 лет Б) 20 лет В) 21 год Г) 22 года Д) 23 года
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 57
|