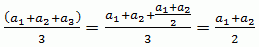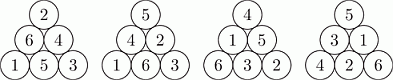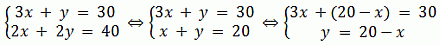Задание 1
|
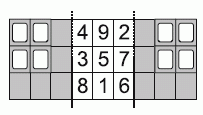
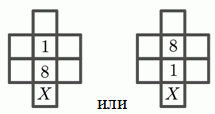
На створках карточки на рисунке, есть прозрачные окошки. Чему равна сумма чисел, которые видны через окошки листовки, когда её створки сложены?
A) 7 Б) 9 В) 12 Г) 14 Д) 15
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 3 = 33
|
Если сложить левую створку, левый столбец и третья строка будут скрыты. Если сложить правую створку, правый столбец будет скрыт, оставив видимыми только две цифры 9 и 5. Их сумма равна
9 + 5 = 14.
Задание 2
|
Основание треугольника увеличили на 50%, а его высоту уменьшили на одну треть. Чему равно отношение площади полученного треугольника к площади исходного треугольника?
A) 2:1 Б) 1:1 В) 1:2 Г) 1:3 Д) 1:4
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Пусть b — основание исходного треугольника, а h — его высота, тогда его площадь равна (b×h)/2.
Основание нового треугольника равно 3/2×b, а его высота — 2/3×h.
Новая площадь равна
1/2 × 3/2×b × 2/3×h = (b×h)/2,
а отношение равно 1:1.
Задание 3
|
В каком из следующих шестиугольников ровно одна треть площади чёрная и ровно половина площади белая?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Если одна треть шестиугольника чёрная, это значит, что 2 треугольника чёрные, и, если одна половина шестиугольника белая, это значит, что 3 треугольника белые. Шестиугольник Д — единственный, который удовлетворяет этим двум условиям.
Задание 4
|
Конкурс «Кенгуру» проводится каждый год в третий четверг марта. Какое самое раннее число может выпасть на этот день?
A) 14 марта
Б) 15 марта
В) 20 марта
Г) 21 марта
Д) 22 марта
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Самая ранняя возможная дата для третьего четверга марта зависит от того, на какой день выпадает первый четверг месяца. Если 1 марта — это четверг, то третий четверг будет 15 марта.
Задание 5
|
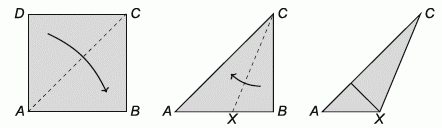
Лёша складывает квадрат по диагонали, получая треугольник. Затем он делает ещё один сгиб так, чтобы одна из коротких сторон этого треугольника легла на его длинную сторону, образуя новый, меньший треугольник AXC. Чему равен угол ∠AXC?
A) 108° Б) 112,5° В) 120° Г) 145° Д) 157,5°
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
По построению ∠CAB = ∠ACB = 45°.
Тогда ∠ACX = 1/2∠ACB = 22,5°.
Наконец, в △AXC, ∠AXC = 180° − ∠CAX − ∠ACX = 180° − 45° − 22,5° = 112,5°
Задание 6
|
Согласно рецепта, для приготовления 1 стакана риса необходимо 1½ стакана воды. Руслан хочет приготовить 1½ стакана риса. Сколько стаканов воды ему нужно?
A) 1 Б) 1¼ В) 1¾ Г) 2¼ Д) 2½
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 33.75 + 3 = 36.75
|
Руслану нужно 1½ × 1½ стакана воды, т е.
3/2 × 3/2 = 9/4 = 2¼.
Задание 7
|
У Лизы есть четыре деревянные цифры, из которых можно составить число 2025. Сколько различных чисел, больших 2025, она может составить из этих цифр?
A) 3 Б) 6 В) 8 Г) 9 Д) 11
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 36.75 - 0.75 = 36
|
Она может составить числа 2052, 2205, 2250, 2502, 2520, 5022, 5202, 5220.
Задание 8
|
В 4-значном числе 80☐☐ отсутствуют последние две цифры. Число делится на 8 и 9. Чему равно произведение этих двух отсутствующих цифр?
A) 6 Б) 16 В) 20 Г) 24 Д) 48
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 36 + 3 = 39
|
Так как 8000 делится на 8, то две последние цифры числа должны образовывать число, которое тоже делится на 8. Кроме того, поскольку число должно делиться на 9, сумма всех его цифр должна быть кратна 9. Эти условия выполняются только для числа 64. Значит, единственное четырёхзначное число, начинающееся с 80 и делящееся и на 8, и на 9, — это 8064. Тогда произведение двух последних цифр равно 24.
Задание 9
|
Лёня держит дома собак, кроликов и кошек. Восемь из его питомцев — не собаки, пять — не кролики, а семь — не кошки. Сколько всего питомцев у Лёни?
A) 10 Б) 11 В) 15 Г) 16 Д) 20
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Пусть R — количество кроликов, С — количество котов, D — количество собак. Тогда,
R + C = 8, D + C = 5, D + R = 7
2(R + C + D) = 20
R + C + D = 10
Ответ — А.
Задание 10
|
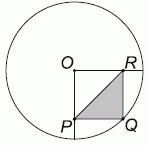
Дана окружность с центром в точке O и радиусом 10 см. Внутри окружности построен квадрат OPQR, где Q — точка на окружности. Чему равна площадь закрашенного треугольника PQR?
A) 12,5 см2
Б) 25 см2
В) 50 см2
Г) 75 см2
Д) 100 см2
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
Проведём OQ. Мы знаем, что OQ = 10 см, так как это радиус. Площадь треугольника PQR равна половине площади OPQR, которая равна (10×10)/2 = 50, следовательно, площадь PQR равна 25 см2
Задание 11
|

У спортсмена есть коллекция из двух золотых и пяти серебряных медалей. Каждая медаль имеет свой номер от 1 до 7. На рисунке показаны 6 чёрно-белых фотографий этих медалей, и известно, что на каждой фотографии есть ровно одна золотая медаль. Чему равна сумма номеров двух золотых медалей?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 37.5 - 1 = 36.5
|
Поскольку на фотографии с медалями 1, 2, 3 есть одно золото и на фотографии с медалями 4, 5, 6 есть одно золото, можно сделать вывод, что 7 — серебро. Аналогичным образом, по фотографиям с тройками медалей 2, 3, 4 и 5, 6, 7, значит, 1 — серебро. Поскольку в 2, 3, 4 есть одно золото и в 6, 7, 1 есть одно золото, можно сделать вывод, что 5 — серебро. Тогда 6 — золото, 4 — серебро, 3 — золото и 2 — серебро.
Наконец, ответ 3 + 6 = 9.

Задание 12
|

Анна смотрит на фотографию на своём смартфоне. Изображение имеет отношение длин сторон 16:9 и заполняет весь экран. Когда она поворачивает смартфон, изображение становится меньше. Какую часть экрана занимает уменьшенная картинка?
A) 3/4 Б) 9/16 В) 27/64 Г) 32/81 Д) 81/256
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 36.5 - 1 = 35.5
|
Ширина фотографии на первой картинке равна длине длинной стороны экрана, а на второй картинке — длине короткой стороны экрана. Из этого следует, что длина фотографии на второй картинке составляет 9/16 от длины фотографии на первой картинке.
Следовательно, фотография на второй картинке занимает (9/16)2 = 81/256 всей площади экрана.
Задание 13
|
Катя и Тимофей сегодня отмечают свои дни рождения. Тимофей заметил, что 1/19 возраста Кати равна 1/17 его возраста. Сумма их возрастов больше 40, но меньше 100. Сколько лет Кате?
A) 19 Б) 34 В) 38 Г) 57 Д) 76
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 35.5 - 1 = 34.5
|
Пусть возрасты Кати и Тимофея равны x и y соответственно. Из условия задачи знаем, что 1/19 возраста Кати равна 1/17 возраста Тимофея, то есть 17x = 19y. Отсюда можно выразить возраст Кати и Тимофея как x = 19k и y = 17k, для некоторого целого числа k. Теперь, используя условие задачи, получаем неравенство:
40 < 17k + 19k = 36k < 100.
Это неравенство выполняется только для k = 2. Следовательно, возраст Кати равен
19 × 2 = 38 лет.
Задание 14
|
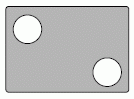
Павел сделал 27 выстрелов по двум мишеням и промахнулся 9 раз. 50% выстрелов, которые он направлял в верхнюю левую мишень, и 80% выстрелов, которые он направлял в нижнюю правую мишень, были успешными. Сколько раз Павел попал в верхнюю левую мишень?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 34.5 + 4 = 38.5
|
Пусть a — количество выстрелов в верхнюю левую мишень, а b — количество выстрелов в нижнюю правую мишень. Тогда
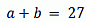 и
и 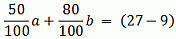
Это приводит к
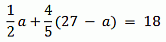
И, следовательно, a = 12. Поэтому ответ —
1/2 а = 1/2 × 12 = 6
Задание 15
|
У Александры есть сумка с 18 шариками, пронумерованными числами от 1 до 18. Какое минимальное количество шариков она должна достать, чтобы быть уверенной, что среди них будет хотя бы три шарика с простыми числами?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 38.5 - 1 = 37.5
|
Существует 7 простых чисел меньше 18: 2, 3, 5, 7, 11, 13 и 17. Чтобы гарантировать, что Александра достанет хотя бы три шарика с простыми числами, она должна сначала достать все шарики с составными номерами, то есть 18 - 7 = 11 шариков. Затем ей нужно достать ещё три шарика с простыми числами. Это значит, что она должна достать 11 + 3 = 14 шариков.
Задание 16
|
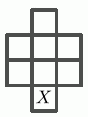
Денис хочет разместить числа от 1 до 8 в ячейках сети на рисунке, по одному числу в каждой ячейке. Он хочет, чтобы ячейки, в которых находятся два последовательных числа, не имели общих сторон или вершин. Какие из чисел Денис может разместить в ячейке, помеченной буквой X?
A) 1 или 8
Б) 2 или 7
В) 3 или 6
Г) 4 или 5
Д) 7 или 8
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 37.5 - 1 = 36.5
|
Числа, занимающие центральные ячейки, должны иметь наименьшее количество цифр-соседей среди возможных, т.е. 1 и 8.
Значит, ни 2, ни 7 не могут находиться ни в одной из ячеек рядов из трёх квадратов, поэтому они должны находиться либо в верхней, либо в нижней ячейке.
Задание 17
|
Число N является наибольшим шестизначным целым числом, произведение всех цифр которого равно 180. Чему равна сумма цифр числа N?
A) 21 Б) 22 В) 23 Г) 24 Д) 25
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 36.5 - 1 = 35.5
|
Известно, что 180 = 22 • 32 • 5.
Поскольку N — наибольшее 6-значное число, а 180 делится на 9, то первая цифра N — 9.
Произведение последних 5 цифр N — 180 : 9 = 20.
Наибольшим делителем 20 является 5, поэтому вторая цифра N — 5.
Произведение последних 4 цифр N — 20 : 5 = 4.
Наибольшим делителем 4 является 4, поэтому последние 4 цифры N — 4, 1, 1 и 1 соответственно.
Тогда возможное значение N равно 954111.
Таким образом, сумма всех цифр числа N равна
9 + 5 + 4 + 1 + 1 + 1 = 21.
Задание 18
|
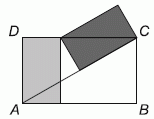
Два закрашенных прямоугольника на рисунке равны. Каждый из них имеет площадь равную 4. Чему равна площадь большого прямоугольника ABCD?
A) 10 Б) 8√3 В) 8 Г) 12 Д) 4√3
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 35.5 - 1 = 34.5
|
Нижний левый серый треугольник равен белому треугольнику в середине (по одной стороне и двум углам). Тогда общая площадь над диагональю искомого прямоугольника равна площади серого прямоугольника + половине площади тёмного прямоугольника (4 + 2 = 6). Это значит, что искомая площадь равна 12.
Задание 19
|
Произведение трёх простых чисел в 11 раз больше их суммы. Найдите наибольшее возможное значение, которое может иметь эта сумма.
A) 14 Б) 17 В) 21 Г) 25 Д) 26
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 34.5 - 1 = 33.5
|
Пусть p, q и r — простые числа, тогда мы имеем
pqr = 11(p + q + r).
Следовательно, одно из простых чисел должно быть 11. Подставляя r в уравнение выше, мы получаем
pq = 11 + p + q.
Если p и q оба больше либо равны 5, мы получим, что левая часть больше правой. Поэтому другое простое число должно быть 2 или 3. Таким образом, мы получаем следующие тройки, удовлетворяющие условию задачи:
(2, 11, 13) и (3, 7, 11)
Следовательно, максимальное значение суммы p + q + r равно 26.
Задание 20
|
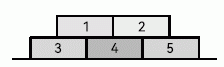
На земле лежат пять кирпичей, как показано на рисунке. Пётр может убрать кирпич только в том случае, если на нём нет других кирпичей. Он убирает по одному кирпичу, выбранному случайным образом, пока на земле не останется ни одного кирпича. Чему равна вероятность того, что кирпич с номером 4 будет убран третьим? (Вероятность равна отношению числа благоприятных исходов к числу всех исходов, если все исходы равновозможны.)
A) 1/3 Б) 1/4 В) 1/5 Г) 1/6 Д) 1/8
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 33.5 - 1 = 32.5
|
Чтобы удалить кирпич №4, нужно сначала убрать кирпичи первого ряда (№1 и №2), что потребует 3 хода.
Первый вариант: Мы начинаем с поднятия кирпича №1. Вероятность этого равна 1/2. Затем обязательно поднимаем кирпич №2, вероятность этого тоже 1/2. Вероятность того, что кирпич №4 будет поднят составляет 1/3. Таким образом, вероятность для этого варианта:
1/2 × 1/2 × 1/3 = 1/12
Второй вариант: Из-за симметрии, если первым будет поднят кирпич №2, то расчёты будут те же.
Поскольку события независимы, общий ответ будет:
1/12 + 1/12 = 1/6
Ответ: вероятность того, что кирпич с номером 4 окажется третьим, который будет поднят, равна 1/6.
Задание 21
|
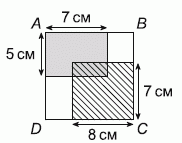
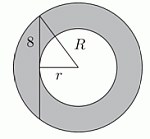
В квадрате ABCD находятся два прямоугольника: один – серый, а другой – заштрихованный. Размеры прямоугольников приведены на рисунке. Площадь их пересечения равна 18 см2. Чему равен периметр квадрата ABCD?
A) 28 см Б) 34 см В) 36 см Г) 38 см Д) 40 см
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 32.5 - 1.25 = 31.25
|
Пусть сторона квадрата ABCD равна x см, тогда стороны прямоугольника, образованного пересечением, равны
(15 − x) см и (12 − x) см.
Имеем
(15 - x)(12 - x) = 18 и
x2 - 27x + 162 = 0
x = 9 см является решением, а периметр квадрата равен
4 × 9 = 36 см2.
Задание 22
|
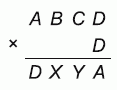
Четырёхзначное число ABCD при умножении на его последнюю цифру D даёт новое четырёхзначное число DXYA, в котором цифры разрядов тысяч и единиц поменялись местами. Сколько существует четырёхзначных чисел ABCD, обладающих таким свойством?
A) 1 Б) 2 В) 9 Г) 10 Д) 11
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 31.25 - 1.25 = 30
|
Цифра A должна совпадать с последней цифрой произведения D2, что определяет несколько возможных пар (A, D). Однако, учитывая, что результат должен быть четырёхзначным числом, мы получаем условия
D ≥ A и D ⋅ A < 10.
Единственная подходящая пара — (A, D) = (1, 9).
Кроме того, должно выполняться B ⋅ D < 10, что даёт два возможных случая:
(A, D) = (1, 9) и B = 0, при этом C может быть любым – 10 чисел – 1009, 1019, 1029, 1039, 1049, 1059, 1069, 1079, 1089, 1099.
(A, D) = (1, 9) и B = 1, но тогда C должно быть равно 0 – 1 число – 1109.
Задание 23
|
Дано шестизначное число ABCDEF, составленное из цифр 1, 2, 3, 4, 5 и 6 без повторений. Оно обладает следующими свойствами: число AB делится на 2, число ABC делится на 3, число ABCD делится на 4, число ABCDE делится на 5, полное число ABCDEF делится на 6. Чему равна цифра F?
A) 2
Б) 4
В) 6
Г) обе цифры 2 и 4 возможны
Д) обе цифры 4 и 6 возможны
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 30 - 1.25 = 28.75
|
Поскольку число ABCDE должно делиться на 5, его пятая цифра может быть только 5 или 0. Число ABCDEF составлено только из цифр 1, 2, 3, 4, 5, 6. Значит, E = 5.
Цифры на втором, четвёртом и шестом местах должны быть 2, 4 или 6, так как они должны быть чётными.
Чтобы число ABC
Далее, число CD должно делиться на 4. Учитывая, что C может быть равно 1 или 3, единственным возможным значением для D является 6.
Получаем, что последняя цифра F должна быть равна 4.
Задание 24
|
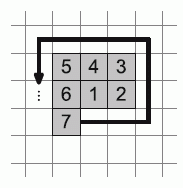
Даниил нумерует клетки в школьной тетрадке. Каждая клетка имеет сторону длиной 0,5 см. Он начинает с клетки, в которую ставит единицу, а затем продолжает нумерацию 2, 3, 4, 5 и так далее, двигаясь против часовой стрелки, как показано на рисунке. Даниил остановился, когда пронумеровал 2025 клеток, и рассматривает фигуру, получившуюся из пронумерованных клеток. Чему равен её периметр?
A) 25 см Б) 45 см В) 80 см Г) 90 см Д) 180 см
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 28.75 + 5 = 33.75
|
На определённом этапе построения фигура, которую строит Даниил, образует квадрат. Найдём наибольшее число, которое является квадратом другого числа и не превышает 2025.
Поскольку 452 = 2025, Даниил останавливается, когда фигура становится квадратом со стороной 45 × 0.5 см.
Тогда её периметр равен 45 × 0.5 × 4 = 90 см.
Задание 25
|
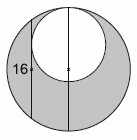
На рисунке два круга касаются внутренним образом. Через точку касания проведён диаметр большего круга. Хорда большего круга параллельна данному диаметру, имеет длину 16 и касается меньшего круга. Найдите площадь серой фигуры.
A) 36 π
Б) 49 π
В) 64 π
Г) 81 π
Д) Недостаточно предоставленной информации
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
Пусть радиус внешнего круга равен R, а радиус внутреннего круга равен r. Тогда площадь заштрихованной области между кругами будет равна
π(R2 − r2).
Чтобы упростить задачу, можно представить, что внутренний круг перенесён в центр внешнего круга, что не изменит площадь заштрихованной области, как показано на рисунке. По теореме Пифагора, разница квадратов радиусов равна
R2 − r2 = 82.
Это означает, что
R2 − r2 = 64.
Таким образом, площадь заштрихованной области будет равна
πR2 − πr2 = 64π.
Задание 26
|
Дана последовательность чисел a1, a2, a3, a4, ... , a10, в которой начиная с третьего элемента, каждый следующий элемент является средним арифметическим всех предыдущих чисел. То есть, a3 – это среднее арифметическое a1 и a2, a4 – это среднее арифметическое a1, a2 и a3, и так далее. Известно, что a1 = 8 и a10 = 6. Чему равно число a2?
A) 28 Б) 32 В) 38 Г) 44 Д) 50
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 32.5 - 1.25 = 31.25
|
Имеем
a3 = 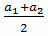 и
и
a4 = 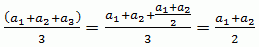
Точно так же будут равны последующие члены последовательности.
Следовательно, a10 = 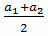 .
.
Таким образом 26 = (8 + a2)/2.
Получаем a2 = 44.
Задание 27
|
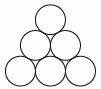
Шесть окружностей расположены в форме треугольника. Иван вписал в них числа от 1 до 6 так, что суммы чисел на всех сторонах этого треугольника оказались одинаковыми. Затем он вычислил сумму чисел в вершинах этого треугольника. Сколько различных значений у него могло получиться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 31.25 - 1.25 = 30
|
Сумма шести вписанных чисел равна
1 + 2 + 3 + 4 + 5 + 6 = 21.
Сумма чисел в вершинах треугольника
не меньше 1 + 2 + 3 = 6,
но не больше 4 + 5 + 6 = 15.
Числа в вершинах входят в суммы чисел на сторонах треугольника дважды. Поэтому сумма этих трёх сумм
не меньше 21 + 6 = 27,
но не больше 21 + 15 = 36,
причём делится на 3, так как это сумма трёх одинаковых чисел.
Тогда сумма чисел в вершинах может принимать только значения 6, 9, 12 и 15.
Следующий пример показывает, что все эти четыре значения возможны.
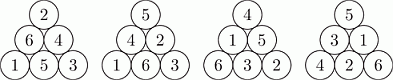
Задание 28
|
На празднике находятся 12 детей, среди которых три пары близнецов. Сколькими способами можно распределить между ними шесть синих и шесть красных шляп, что бы каждому близнецу в паре достались шляпы одного цвета?
A) 72 Б) 86 В) 92 Г) 102 Д) 132
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 30 - 1.25 = 28.75
|
Рассмотрим два возможных случая распределения шляп:
Случай 1: Все три пары близнецов носят шляпы одного цвета.
У нас есть 2 варианта: все в красных или все в синих шляпах.
Случай 2: Две пары близнецов носят шляпы одного цвета, а третья пара — другого.
Выбираем две пары, которые получат один и тот же цвет, — это можно сделать 3 способами.
Оставшиеся 6 детей (не близнецы) должны получить 2 шляпы того же цвета, что и две выбранные пары. Эти 2 шляпы можно распределить между 6 детьми следующим образом:
выбираем первого ребенка (6 вариантов), затем второго (5 вариантов), но так как порядок не имеет значения, делим на 2:
6 ∙ 5 : 2 = 15.
Так как шляпы могли быть и красными, и синими, умножаем результат на 2.
Общее количество способов:
2 + 2 • 3 • 15 = 92.
Задание 29
|
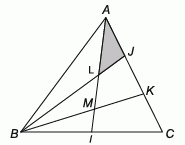
Площадь треугольника ABC равна 60. Точка I является серединой стороны BC, а точки J и K делят сторону AC на три равных отрезка. Точка L является точкой пересечения AI и BJ. Чему равна площадь треугольника ALJ?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 28.75 - 1.25 = 27.5
|
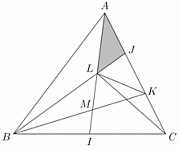
Треугольники AJL, JLK и KLC имеют равные площади, обозначим их за x. Площади треугольников LIB и LCI обозначим за y.
Поскольку AI является медианой, она делит треугольник ABC на два равновеликих треугольника.
S∆AIC = 1/2 S∆ABC = 30.
3x + y = 30.
Т. к. AJ = JK = KC,
S∆BJC = 2/3 S∆ABC = 40.
2x + 2y = 40.
Решаем систему уравнений:
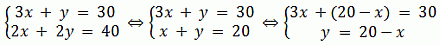
2x = 10
x = 5
y = 20 - 5 = 15
S∆AJL = x = 5
Задание 30
|

Анастасия заполняет таблицу 2 × 4 числами от 1 до 8. При этом каждое число должно быть меньше, чем число справа от него, и меньше, чем число под ним. Сколькими способами она может это сделать?
A) 6 Б) 8 В) 10 Г) 12 Д) 14
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 27.5 - 1.25 = 26.25
|
Поскольку число 1 является наименьшим, оно должно находиться в верхнем левом углу таблицы. Аналогично, число 8, как наибольшее, должно стоять в нижнем правом углу. Числа 2 и 7 могут располагаться двумя способами, что задаёт разные варианты заполнения таблицы.

В первом случае оставшиеся четыре числа можно разместить в каждой строке в порядке возрастания, выбирая по два числа из четырёх возможных. Таких вариантов 6.
Во втором случае число 6 должно находиться в нижнем ряду во второй ячейке справа. Число над ним можно выбрать тремя способами, а оставшиеся два числа занимают оставшиеся ячейки в порядке возрастания. Получаем 3 варианта заполнения.
Третий случай аналогичен второму, также имеет 3 возможных варианта заполнения.
В четвёртом случае числа 3 и 6 должны быть записаны в конкретные ячейки, а два оставшихся числа можно разместить двумя способами, что даёт 2 варианта.
Таким образом, общее количество способов заполнения таблицы равно:
6 + 3 + 3 + 2 = 14.






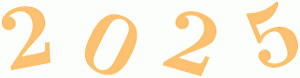





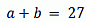 и
и 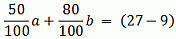
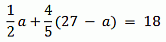



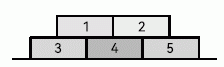

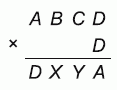



 и
и