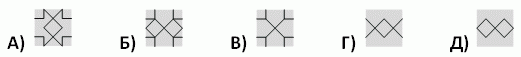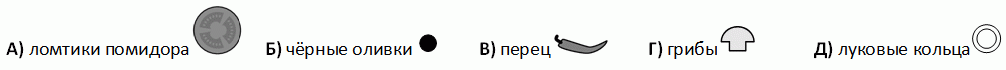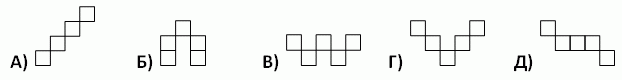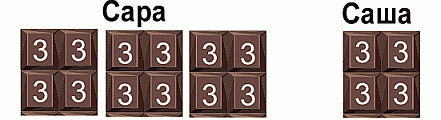Задание 1
|
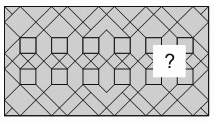
Какой из следующих фрагментов завершает узор?
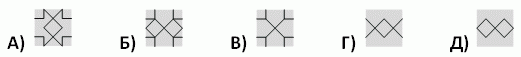
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 30 - 0.75 = 29.25
|
Задание 2
|
Аня из кубиков построила стену, на которой отображается год 2025. Белла стоит с обратной стороны стены. Что она видит?

|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 29.25 - 0.75 = 28.5
|
С обратной стороны 0 остается неизменным, 2 превращается в 5, а 5 превращается в 2.
Задание 3
|
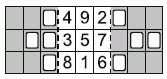
У Миши есть карточка с числами и отверстиями на створках с обеих сторон, как показано на рисунке. Он складывает правую створку по пунктирной линии и видит цифры 2, 3, 5 и 6 через отверстия. Затем он складывает левую створку по другой пунктирной линии. Чему равна сумма чисел, которые он видит сейчас?
A) 10 Б) 12 В) 14 Г) 9 Д) 8
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 28.5 - 0.75 = 27.75
|
Когда сложена правая створка, через отверстия видны числа 2, 3, 5 и 6. Когда сложены обе створки, видны два числа — 5 и 3, их сумма — 8.
Задание 4
|

На белый куб наклеили серые узоры, как показано на рисунке. Все грани куба выглядят одинаково. Сколько всего серых квадратов наклеено на куб?
A) 30 Б) 18 В) 16 Г) 15 Д) 14
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 27.75 - 0.75 = 27
|
На одной грани 1 целый квадрат и 4 половинки квадрата, что в сумме даёт 3 квадрата. У куба 6 граней, всего: 6 • 3 = 18 квадратов.
Задание 5
|
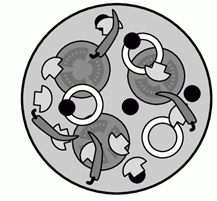
Эмиль положил ломтики помидора, чёрные оливки, перцы, грибы и луковые кольца на пиццу, но не обязательно в этом порядке. Каждый раз он клал все дольки одного ингредиента, затем – следующего. В результате получилась пицца, показанная на рисунке. Какую начинку Эмиль положил на пиццу третьей?
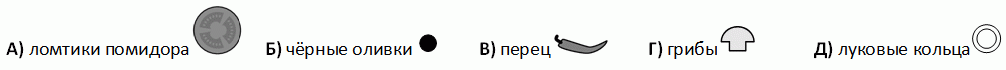
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 27 - 0.75 = 26.25
|
Сначала Эмиль положил ломтики помидора, затем кольца лука, чёрные оливки, грибы и в последнюю очередь он положил перец. Таким образом, третьим ингредиентом были чёрные оливки.
Задание 6
|
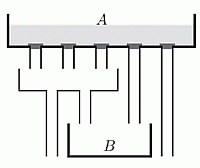
В контейнере A находилось 10 литров воды. Все пять пробок на дне контейнера A вынули одновременно, и вся вода вытекла. Какой объём воды оказался в контейнере B?
A) 3 литра Б) 4 литра В) 5 литров Г) 6 литров Д) 8 литров
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 26.25 - 0.75 = 25.5
|
(1/2 • 3/5 + 1/5) • 10 л = 5 л
Альтернативное решение:
В первые 5 труб вытекает по 2 л воды в каждую. Через три трубы с левой стороны в сумме проходит 6 л. Эти 6 л распределяются между двумя новыми трубами, по 3 л на каждую. В две трубы справа поступает по 2 л воды в каждую. Таким образом, в контейнере B окажется:
3 л + 2 л = 5 л.
Задание 7
|
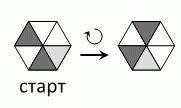
Тая вращает бумажный шестиугольник, разделённый на шесть равных частей. За один поворот шестиугольник поворачивается по часовой стрелке на одну часть. Исходный шестиугольник и результат первого поворота показаны на схеме. Каким будет вид шестиугольника после восьми поворотов?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 25.5 + 3 = 28.5
|
Поскольку 8 дает остаток 2 при делении на 6, бумажный шестиугольник поворачивается на один полный оборот, а затем еще на два поля.
Задание 8
|

Меню бургерной было написано мелом на доске. Но дождь смыл некоторые цифры. Названия бургеров расположены в порядке возрастания цены. Какая из следующих цен может быть ценой одного из бургеров?
A) 4.10 Б) 5.50 В) 5.60 Г) 6.30 Д) 6.60
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 28.5 - 0.75 = 27.75
|
Можно увидеть, что классический бургер стоит не менее 4,30, бургер с беконом — не менее 4,60, сырный — не менее 5,50, а двойной бургер — не менее 6,10. Если бы любой из этих бургеров был дороже, то бургер цезарь стоил бы не менее 7,10, а это не так. Следовательно, цены четырёх бургеров в середине составляют 4,30, 4,60, 5,50 и 6,10.
Задание 9
|
Шестеро детей приняли участие в гонке. Ариана заняла третье место. Белла пересекла финиш шестой, сразу за Егором. Мария в итоговом зачёте оказалась между Арианой и Егором. Диана обогнала Кирилла прямо перед финишем. Кто выиграл гонку?
A) Ариана Б) Кирилл В) Диана Г) Егор Д) Мария
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 27.75 + 3 = 30.75
|
Из условия следует, что Aриана на третьем месте, Егор на пятом и Белла на шестом месте. Тогда Мария должна быть между Арианой и Егором, то есть на четвёртом месте. Так как Диана обгоняет Кирилла, Диана — победитель, а Кирилл — второй. Порядок на финише: Диана, Кирилл, Ариана, Мария, Егор, Белла.
Задание 10
|
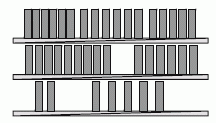
В книжном стеллаже 3 полки. На верхней полке 17 книг, на средней – 15, на нижней – 7. Моника хочет, чтобы на всех полках было одинаковое количество книг. Она также хочет переместить как можно меньше книг. Сколько книг Моника должна переместить со средней полки на нижнюю?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30.75 + 3 = 33.75
|
Всего на полках
17 + 15 + 7 = 39 книг.
Значит, на каждой полке должно быть
39 : 3 = 13 книг.
Переместим 4 книги с верхней полки и 2 книги со средней полки на нижнюю полку. Теперь на каждой полке по 13 книг. Мы переместили 2 книги со средней полки на нижнюю.
Задание 11
|
Три черепахи участвуют в забеге на 10 километров. Каждая из них движется с постоянной скоростью. Когда первая черепаха финишировала, вторая прошла 1/4 дистанции, а третья – 1/5 дистанции. На каком расстоянии от финиша будет третья черепаха, когда финиширует вторая?
A) 1 км Б) 2 км В) 3 км Г) 4 км Д) 5 км
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 33.75 - 1 = 32.75
|
Когда вторая черепаха преодолеет 1/4 дистанции, третья черепаха преодолеет 1/5 дистанции. Второй черепахе осталось преодолеть расстояние в три раза больше, чем она уже прошла. За время, пока вторая черепаха достигнет финиша, третья черепаха ещё три раза пройдёт 1/5 дистанции. Таким образом, у третьей черепахи остаётся 1/5 дистанции до финиша, когда финиширует вторая черепаха.
10 км : 5 = 2 км.
Альтернативное решение:
Когда первая черепаха достигнет финишной черты на 10 км, вторая черепаха преодолеет четверть дистанции, то есть 2,5 км, третья черепаха преодолеет 2 км. Второй черепахе нужно в четыре раза больше времени, чем первой, чтобы преодолеть 10 км. Когда вторая черепаха достигнет финишной черты, третья черепаха преодолеет 4 • 2 км = 8 км, то есть она будет в 2 км от финишной черты.
Задание 12
|

Вера построила башню из шести кубиков и решила записать на них числа так, чтобы выполнялось следующее условие. Если подниматься снизу вверх, то числа будут увеличиваться не менее чем на 2. Четыре числа она уже вписала, как показано на рисунке. Сколько существует способов записать числа на двух оставшихся кубиках?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 32.75 - 1 = 31.75
|
Возможные варианты: 8 и 10, 8 и 11, 8 и 12, 9 и 11, 9 и 12, 10 и 12. Итак, всего 6 вариантов.
Задание 13
|
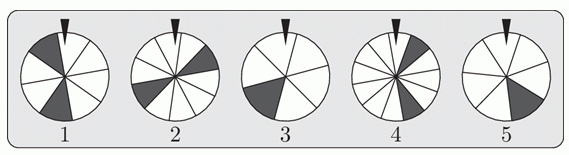
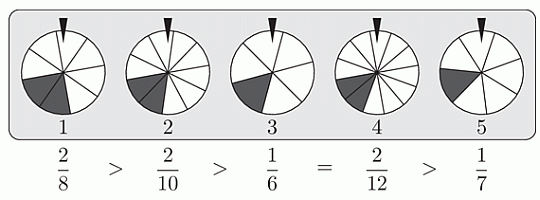
На рисунке изображены пять колёс фортуны. Каждое колесо разделено на разное количество одинаковых частей. Вы получите приз, если повернёте колесо, и оно остановится так, что треугольник над колесом укажет на заштрихованную часть. Какое колесо даёт наибольшие шансы на победу?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 31.75 + 4 = 35.75
|
Задание 14
|

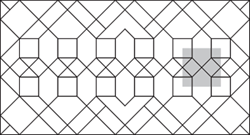
Какую из следующих фигур (в исходном или повёрнутом виде) нельзя разместить на белых клетках данного квадрата?
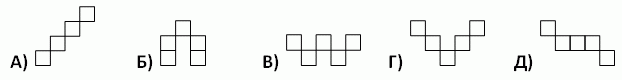
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 35.75 - 1 = 34.75
|
На рисунке показаны варианты размещения фигур А, Б, В и Д.

Задание 15
|

Команда школы по плаванию готовится к эстафете. Пять пловцов проплыли одну и ту же дистанцию друг за другом. На рисунке показано время на секундомере тренера, показывающее, когда каждый пловец завершил свой этап. Первому пловцу потребовалось на это 2 минуты и 8 секунд. Какой пловец проплыл свою дистанцию быстрее всех?
A) первый Б) второй В) третий Г) четвёртый Д) пятый
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 34.75 - 1 = 33.75
|
Первому пловцу нужно на 8 с больше, чем 2 мин, второму пловцу нужно на 1 с меньше, чем 2 мин, третьему пловцу нужно на 3 с больше, чем 2 мин, четвёртому пловцу нужно на 5 с меньше, чем 2 мин, пятому пловцу нужно на 2 с меньше, чем 2 мин. Значит, четвёртому пловцу (вариант Г) потребовалось меньше всего времени.
Задание 16
|
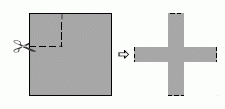
Жанна вырезает четыре одинаковых квадрата из углов квадратного листа бумаги, как показано на рисунке. Общая площадь отрезанных частей составляет 16 см2, а площадь оставшегося креста составляет 9 см2. Чему равен периметр креста в см?
A) 9 Б) 16 В) 20 Г) 25 Д) 32
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 33.75 - 1 = 32.75
|
Площадь листа равна
16 см2 + 9 см2 = 25 см2,
поэтому длина стороны квадрата равна 5 см, а его периметр равен
4 • 5 см = 20 см.
Периметр креста равен периметру квадрата.
Задание 17
|
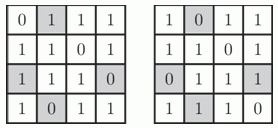
На каждой из карточек, показанных ниже, написаны два трёхзначных числа. Но некоторых цифр не видно, так как на карточки пролились чернила. На одной из карточек сумма цифр обоих чисел одинакова. На какой карточке расположены эти два числа?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32.75 + 4 = 36.75
|
В варианте A 5 + 4 + 3 = 12, поэтому для второго числа нужно ещё 12 - 1 - 1 = 10, что не является цифрой, поэтому эта карточка не подходит. По аналогии не подходят варианты Б, Г, Д. Но для варианта В могут быть числа 982 и 199 (выбор уникален).
Задание 18
|

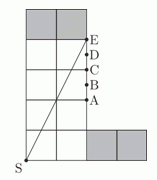
Фигура на рисунке состоит из одинаковых квадратов. Точка B – середина отрезка AC, а точка D – середина CE. Мария хочет разрезать фигуру по прямой на две части равной площади. Какую из точек A, B, C, D или E она должна соединить разрезом с точкой S, чтобы это сделать?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 36.75 - 1 = 35.75
|
Задание 19
|

Алексей хочет вписать числа 0 или 1 в каждой ячейке таблицы так, чтобы во всех строчках, столбцах и обеих диагоналях сумма чисел была равна 3. Он уже вписал 0 в одной из ячеек, как показано на рисунке. Какой будет сумма чисел в ячейках, отмеченных вопросительным знаком «?», когда Алексей заполнит всю таблицу?
A) 1 Б) 2 В) 3 Г) 4 Д) нельзя вычислить
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 35.75 + 4 = 39.75
|
Поскольку 0 уже размещен, все остальные ячейки во второй строке, третьем столбце и диагонали, проходящей через ячейку с 0, должны быть заполнены числом 1.

Если теперь поместить 0 или 1 в одну из ячеек с вопросительным знаком и заполнить остальные ячейки, сумма всех ячеек с вопросительными знаками будет равна 2.
Задание 20
|
Маша и Паша записали по три трёхзначных числа, используя все цифры от 1 до 9 ровно по одному разу. Затем они расположили свои числа в порядке возрастания. Оказалось, что среднее число Маши является наибольшим возможным среди значений, которое может иметь среднее число. А у Паши наоборот: среднее число является наименьшим возможным. Чему равна разность между этими числами Маши и Паши?
A) 642
Б) 684
В) 864
Г) 888
Д) ни один из предложенных вариантов
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 39.75 - 1 = 38.75
|
Разряд сотен наибольшего среднего числа не может быть 9, потому что тогда не останется подходящей цифры для большего трёхзначного числа. Следовательно, наибольшее среднее число должно начинаться с 8, оставляя 9 для большего числа. Таким образом, становится ясно, что наибольшее среднее число — 876. Аналогично, наименьшее среднее число — 234. Их разность равна 876 - 234 = 642.
Задание 21
|
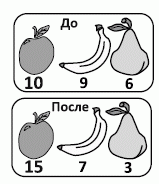
У ведьмы было 10 яблок, 9 бананов и 6 груш. Однажды она с помощью магии превратила каждый из этих фруктов во фрукт другого из двух данных видов. Например, она превратила каждое яблоко либо в банан, либо в грушу. Теперь у нее 15 яблок, 7 бананов и 3 груши. Сколько всего яблок ведьма превратила в бананы?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 38.75 + 5 = 43.75
|
Обратите внимание, что количество бананов и груш до превращения в общей сложности равно 9 + 6 = 15, что в точности равно количеству яблок после превращения. Это означает, что ВСЕ бананы и груши превратились в яблоки. Например, ни один банан не превратился в грушу, потому что тогда 9 бананов и 6 груш дали бы меньше, чем 9 + 6 = 15 яблок, что не так. Аналогично, ни одна груша не превратилась в банан. (Это второе решающее наблюдение) поскольку ни один банан раньше не был грушей, и ни одна груша раньше не была бананом, следовательно, все бананы и все груши раньше были яблоками. В частности, 7 бананов были превращены из яблок, что и является ответом.
Задание 22
|
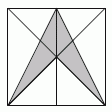
Длина стороны квадрата, изображенного на рисунке, составляет 10 см. Линия, проведённая через центр квадрата, делит его на два равных прямоугольника. Чему равна площадь серой части квадрата?
A) 12,5 см2 Б) 25 см2 В) 30 см2 Г) 40 см2 Д) 50 см2
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 43.75 - 1.25 = 42.5
|
Площадь квадрата 10 см • 10 см = 100 см2
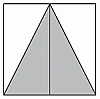
100 см2 : 2 = 50 см2
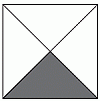
100 см2 : 4 = 25 см2
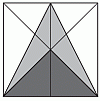
50 см2 - 25 см2 = 25 см2
Задание 23
|

Оля хочет разделить фигуру на рисунке на 5 одинаковых частей, так чтобы каждая часть состояла из 3 клеток. Какая из клеток, отмеченных буквами, окажется в одной части с клеткой, отмеченной звёздочкой?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 42.5 - 1.25 = 41.25
|
Задание 24
|
Фёдор никогда не говорит правду по вторникам, четвергам и субботам. Он всегда говорит правду в остальные четыре дня недели.
Однажды у Матвея состоялся следующий разговор с Фёдором:
Матвей: «Какой сегодня день недели?»
Фёдор: «Суббота».
Матвей: «Какой будет завтра день недели?»
Фёдор: «Среда».
В какой день состоялся этот разговор?
A) понедельник Б) вторник В) среда Г) четверг Д) пятница
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 41.25 - 1.25 = 40
|
Оба ответа противоречат друг другу, поэтому это один из дней, в который Фёдор лжет (вторник, четверг или суббота). Следовательно, оба утверждения неверны. Это не может быть суббота или день перед средой, то есть вторник, потому что Фёдор лжёт. Следовательно, единственный возможный оставшийся день — четверг. Оба утверждения Фёдора неверны, ответ — четверг.
Задание 25
|
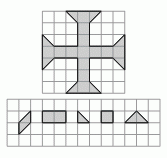
Иван хочет построить фигуру в виде креста, изображённую на рисунке, используя детали, которые изображены под крестом. У него есть много копий каждой детали, и он может поворачивать их при необходимости. Детали не должны перекрывать друг друга. Какое минимальное количество деталей нужно Ивану для построения этой фигуры?
A) 11 Б) 12 В) 13 Г) 15 Д) 17
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 40 - 1.25 = 38.75
|
Задание 26
|
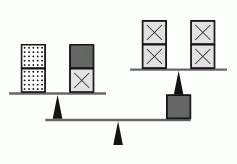
На рисунке показано, как некоторые блоки уравновешены на весах. Блоки, окрашенные одинаково, имеют одинаковый вес, а окрашенные по-разному – разный вес. Виктор расставил в ряд три блока разных типов в порядке убывания веса. Что у него получилось?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 38.75 + 5 = 43.75
|
Сравним левую и правую стороны весов. Видно, что два точечных блока весят столько же, сколько три блока с перекрещенными линиями. Значит, точечные блоки тяжелее.
На левой стороне видно, что серый блок и блок с перекрещенными линиями вместе весят столько же, сколько два точечных блока. Так как блок с перекрещенными линиями легче, серый блок должен быть тяжелее точечного.
Итак, самый тяжёлый — серый блок, за ним идёт точечный, а самый лёгкий — блок с перекрещенными линиями. Ответ — A.
Задание 27
|
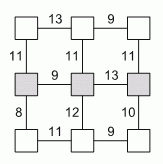
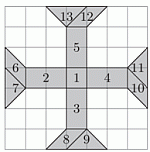
Патриция хочет вписать числа от 1 до 9 в квадраты на схеме, по одному числу в каждом квадрате. Она хочет, чтобы сумма чисел в любых двух соседних квадратах была равна числу на линии, соединяющей эти квадраты. Чему равна сумма чисел, которые она должна вписать в серые квадраты?
A) 16 Б) 17 В) 18 Г) 20 Д) 21
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 43.75 - 1.25 = 42.5
|
Если квадрат содержит 1, то сумма в любой паре квадратов, содержащих этот квадрат ≤ 10. Единственный квадрат с таким свойством — в нижнем правом углу. Поэтому положение числа 1 определено однозначно. Затем мы можем заполнить остальные квадраты исходя из сумм, указанных на линиях.
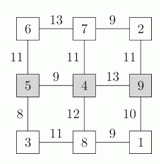
Сумма равна 5 + 4 + 9 = 18.
Задание 28
|
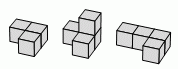
Какую из следующих конструкций можно собрать из блоков, указанных на рисунке?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 42.5 + 5 = 47.5
|
Вариант А невозможен, потому что по крайней мере один из кубиков на верхнем уровне должен быть из второго блока. Но тогда не останется места для двух других кубиков.
Вариант Б невозможен, потому что на верхнем уровне должен быть по крайней мере 1 кубик из второго блока.
Вариант В невозможен, потому что кубик на верхнем уровне должен быть из второго блока, и тогда не остаётся места для двух других блоков.
Вариант Г возможен, один кубик из второго блока и один кубик из третьего блока находятся на верхнем уровне.
Вариант Д невозможен, потому что на верхнем уровне может быть не более 3 групп кубиков.
Задание 29
|
У Сары было в три раза больше шоколадок, чем у Саши. Затем Сара отдала четверть своих шоколадок Саше. Сейчас у Сары на шесть шоколадок больше, чем у Саши. На сколько шоколадок у Сары было больше, чем у Саши первоначально?
A) 36 Б) 30 В) 27 Г) 24 Д) 20
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 47.5 - 1.25 = 46.25
|
У Сары было в три раза больше шоколадок, чем у Саши.
Так как Сара отдала четверть своих шоколадок Саше, разделим каждую шоколадку на четыре части.

Сара выбрала четверть своих шоколадок.

Сара отдала четверть своих шоколадок Саше.

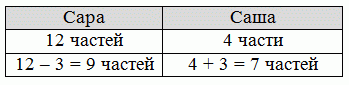
У Сары все еще на 6 шоколадок больше, чем у Саши.
Разница (которая составляет 9 − 7 = 2 части) соответствует 6 шоколадкам. Таким образом, каждая часть соответствует 3 шоколадкам.
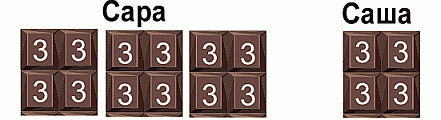
Следовательно, у Сары и Саши изначально было
12 • 3 = 36 и 4 • 3 = 12 соответственно, что дает разницу
36 − 12 = 24.
Задание 30
|
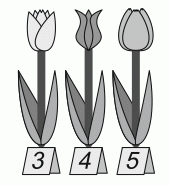
Зоя хочет купить цветы и составить из них букет. Цены (в руб) трёх видов цветов, которые она может купить, показаны на рисунке. Сколько разных букетов стоимостью ровно 23 руб каждый она может купить?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 46.25 - 1.25 = 45
|
Возможны 7 решений:
2 • 3 + 3 • 4 + 1 • 5 = 23
1 • 3 + 5 • 4 = 23
1 • 3 + 4 • 5 = 23
6 • 3 + 1 • 5 = 23
3 • 3 + 1 • 4 + 2 • 5 = 23
2 • 4 + 3 • 5 = 23
5 • 3 + 2 • 4 = 23