"Кенгуру-2025"
20 марта 2025
Задание для 3-4 классов
Участник: Войтик Ренат, СШ №140, Фрунзенский район г. Минска
На старте каждый участник получает 24 балла
Задание 1
Маша строит куб 3 × 3 × 3 из единичных кубиков, добавляя их по одному. По ходу работы она сделала 5 различных фотографий. Какая из следующих пяти фотографий была сделана четвёртой по ходу строительства?

Правильный ответ: А
Ответ участника: В
Промежуточный результат: 24 - 0.75 = 23.25
Пока Маша строит большой куб, количество маленьких кубиков становится всё больше и больше. Таким образом, её фотографии были сделаны в следующем порядке:
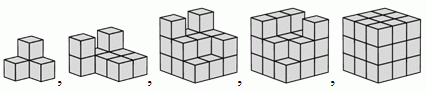
или: Г, Б, Д, А, В. Её четвертая фотография выглядит как А

Задание 2
Симона вписывает цифры 2, 0, 2, 5 в квадратики на рисунке.
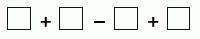
В каком порядке их следует вписать, чтобы значение полученного выражения было наибольшим?
A) 0, 2, 2, 5
Б) 0, 5, 2, 2
В) 2, 5, 2, 0
Г) 5, 0, 2, 2
Д) 5, 2, 0, 2
Правильный ответ: Д
Ответ участника: Г
Промежуточный результат: 23.25 - 0.75 = 22.5
Одна из цифр вычитается, а остальные три цифры складываются. Таким образом, результат будет наибольшим, когда вычитаемая цифра будет наименьшей, т.е. 0.
Также можно вычислить все пять результатов, чтобы найти наибольший:
A) 0 + 2 - 2 + 5 = 5
Б) 0 + 5 - 2 + 2 = 5
В) 2 + 5 - 2 + 0 = 5
Г) 5 + 0 - 2 + 2 = 5
Д) 5 + 2 - 0 + 2 = 9
Задание 3

Лариса раскручивает свою вертушку. Какой из следующих является её вертушка?

Правильный ответ: Д
Ответ участника: Д
Промежуточный результат: 22.5 + 3 = 25.5
В вертушке есть два черных поля друг напротив друга. Это можно увидеть только в вариантах В, Г и Д. Серое поле в вертушке находится следующим по часовой стрелке после чёрного поля. Это можно увидеть только в варианте Д, который является решением.
Задание 4
Какая из следующих верёвок завяжется в узел, если потянуть её за концы?
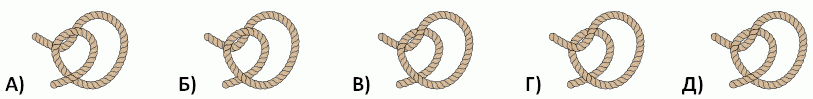
Правильный ответ: Д
Ответ участника: Б
Промежуточный результат: 25.5 - 0.75 = 24.75
Чтобы сформировать узел, верёвка должна создать затягивающуюся петлю (один конец проходит под другим, затем над, а затем снова под). Это выполняется только веревкой Д.
Задание 5
На обычном игральном кубике общее количество точек на двух противоположных гранях всегда равно 7. Какой из следующих игральных кубиков может быть обычным игральным кубиком?

Правильный ответ: А
Ответ участника: Г
Промежуточный результат: 24.75 - 0.75 = 24
На обычной игральной кости общее количество точек на двух противоположных гранях всегда равно 7. Это означает, что 1 и 6 находятся на противоположных гранях, 2 и 5 находятся на противоположных гранях, и 3 и 4 находятся на противоположных гранях. В вариантах Б и Д 2 и 5 находятся на соседних гранях. В варианте В 1 и 6 находятся на соседних гранях. В варианте Г 3 и 4 находятся на соседних гранях. Таким образом, кости в вариантах Б, В, Г, Д не являются обычными игральными костями. В варианте A мы видим только одно из чисел 1 и 6, 2 и 5 и 3 и 4, поэтому для каждой из этих пар другое число может быть на противоположной грани. Только вариант A может быть нормальной игральной костью.
Задание 6
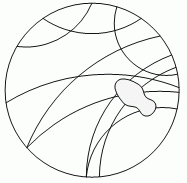
В круге на полу нарисованы линии. Александра ступила одной ногой в этот круг. Какие линии накрыл её след?

Правильный ответ: Б
Ответ участника: Б
Промежуточный результат: 24 + 3 = 27
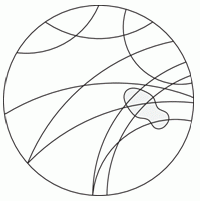
Если соединить пути, как показано на рисунке, то будет видно, что Б является правильным ответом.
Задание 7
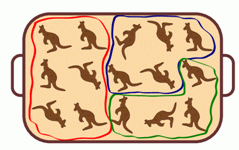
Кенгуру Кеша прыгает из школы в зоопарк по схеме:
↑ 2, ↖ 2, ↙ 1, ← 4,
как показано на рисунке.
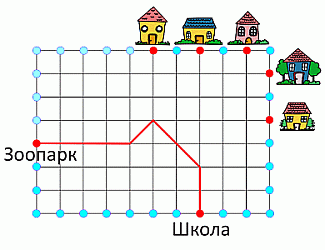
Затем он прыгает из зоопарка по схеме:
→ 3, ↗ 2, ↑ 2.
В какой домик он попадёт?
Правильный ответ: А
Ответ участника: А
Промежуточный результат: 27 + 3 = 30
Начинаем с зоопарка, рисуем путь, который проходит кенгуру согласно инструкции.

Он доберётся до дома А.
Задание 8

Какую вертушку может построить Егор из данных трёх стержней?

Правильный ответ: Д
Ответ участника: А
Промежуточный результат: 30 - 0.75 = 29.25
У стержня с двумя зелёными треугольниками оба треугольника находятся на одной стороне. Стержень с двумя зелёными треугольниками есть в вариантах А, Б, Г и Д. В вариантах А, Б и Г треугольники находятся на разных сторонах этого стержня, поэтому эти вертушки невозможны. Только вертушка варианта Д сделана из 3 стержней, которые есть у Егора.
Задание 9
Никита и его младшая сестра расплачиваются ракушками и шариками в своем магазине игрушек. Каждая ракушка стоит 6 руб, а каждый шарик – 1 руб. Какой из следующих наборов стоит 16 руб?

Правильный ответ: Д
Ответ участника: Д
Промежуточный результат: 29.25 + 4 = 33.25
Вычислим стоимость для каждой коллекции.
А) 2 ракушки имеют стоимость 2 × 6 = 12, поэтому общая стоимость равна
12 + 1 = 13.
Б) ракушка стоит 6, поэтому общая стоимость
6 + 9 = 15.
В) 3 ракушки стоят
3 × 6 = 18.
Г) ракушка стоит 6, поэтому общее стоимость равна
6 + 5 = 11.
Д) 2 ракушки имеют стоимость 2 × 6 = 12, поэтому общая стоимость равна
12 + 4 = 16.
Д - это решение.
Задание 10
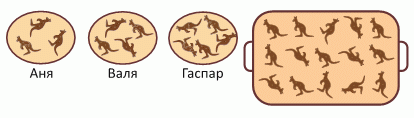
У Ани, Вали и Гаспара на тарелках лежали печенья в виде кенгуру, как показано на рисунке. Затем они разделили оставшиеся 15 печений на подносе так, что у всех на тарелках количества печений стали одинаковыми. Сколько печений с подноса досталось Ане?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
Правильный ответ: В
Ответ участника: Б
Промежуточный результат: 33.25 - 1 = 32.25
У Ани, Вали и Гаспара уже есть 3, 4 и 5 печений. Если мы положим еще 2 печенья на тарелку Ани и ещё 1 печенье на тарелку Вали, у всех на тарелках будет одинаковое количество печений. Теперь все ещё остается
15 − 2 − 1 = 12 печений, которые нужно поровну разделить между тремя детьми.
Таким образом, каждый из них получает ещё 12 : 3 = 4 печенья.
Это значит, что в общей сложности Аня должна получить 2 + 4 = 6 печений.
Другое решение - сначала подсчитать, сколько печений получает каждый ребенок в общей сложности. У них уже есть 3, 4 и 5 печений. Вместе с 15 печеньями получается
3 + 4 + 5 + 15 = 27 печений.
Таким образом, в конце у каждого ребенка должно быть
27 : 3 = 9 печений.
Это значит, что Аня должна получить ещё 9 − 3 = 6 печений.
Задание 11
Утром у 5 друзей были одинаковые полностью заряженные мобильные телефоны. К вечеру Боря проговорил по телефону столько же, сколько Аня и Вика вместе взятые. В результате у Бори закончилась зарядка. Дима вообще не пользовался своим телефоном. Какой могла оказаться зарядка на телефоне Гриши?
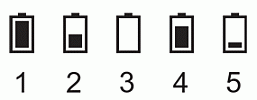
A) 1 Б) 2 В) 3 Г) 4 Д) 5
Правильный ответ: Б
Ответ участника: Г
Промежуточный результат: 32.25 - 1 = 31.25
Поскольку у Бори закончилась зарядка, его телефон — телефон 3. Дима вообще не пользовался своим телефоном, поэтому его телефон — телефон 1. Только для телефонов 4 и 5 сумма зарядов батарей равна полному заряду, поэтому они должны принадлежать Ане и Вике. Остаётся телефон 2, он принадлежит Грише.
Задание 12
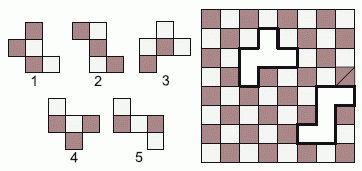
Из клетчатого квадрата вырезали две фигуры, как показано на рисунке. Какими из следующих пяти были эти две фигуры?
A) 1 и 2
Б) 1 и 5
В) 3 и 4
Г) 3 и 5
Д) 4 и 5
Правильный ответ: Б
Ответ участника: Б
Промежуточный результат: 31.25 + 4 = 35.25
Поворачиваем фигуры 1, 3 и 4 так, чтобы 3 квадрата в ряду были горизонтальными. Таким образом, мы видим, что только 1 и 3 помещаются в отверстие сверху, и только 1 имеет правильную окраску. Аналогично, мы поворачиваем фигуры 2 и 5 так, чтобы 3 квадрата в ряду были вертикальными. Получаем, что только 5 помещается в отверстие справа (и что окраска правильная). Фигуры 1 и 5 завершают шахматную доску.
Задание 13

В зоопарке Рада кормила 6 овец. Она дала им в общей сложности 210 грамм сухого корма. Самой маленькой овце досталось в два раза больше корма, чем любой другой овце. Сколько корма получила самая маленькая овца?
A) 55 г Б) 60 г В) 70 г Г) 75 г Д) 80 г
Правильный ответ: Б
Ответ участника: А
Промежуточный результат: 35.25 - 1 = 34.25
Самая маленькая овца получает в два раза больше еды, поэтому мысленно заменим её двумя обычными овцами. Тогда у нас есть
5 + 2 = 7 овец.
Так как 210 : 7 = 30, каждая овца получает 30 грамм еды. Это означает, что самая маленькая овца получает
2 × 30 = 60 грамм еды.
Другое решение — начать с того, чтобы дать каждой овце 10 грамм. Самая маленькая овца получает 20 грамм. Тогда общее количество еды теперь равно:
20 + 10 + 10 + 10 + 10 + 10 = 70 грамм.
Мы делаем это снова и теперь даём 70 + 70 = 140 грамм в общей сложности.
Мы делаем это ещё раз и теперь даём 140 + 70 = 210 грамм.
Итак, в общей сложности мы дали большим овцам 3 × 10 = 30 грамм, а самой маленькой овце 2 × 30 = 60 грамм еды.
Задание 14
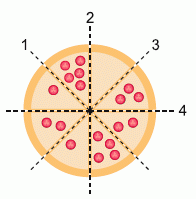
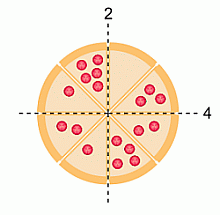
Тимур хочет разрезать пиццу на 2 половины так, чтобы на каждой половине оказалось одинаковое количество помидоров. Он может сделать это двумя разными способами. По каким линиям он может резать?
A) 1 и 3
Б) 1 и 4
В) 2 и 3
Г) 2 и 4
Д) 3 и 4
Правильный ответ: Г
Ответ участника: Б
Промежуточный результат: 34.25 - 1 = 33.25
Начнем с разреза 1 и посчитаем помидоры с обеих сторон.
Над ним
5 + 3 + 2 = 10 помидоров, а под ним
4 + 1 + 2 + 1 = 8 помидоров.
Разрез 2 дает
5 + 1 + 2 + 1 = 9 и
0 + 3 + 2 + 4 = 9 помидоров на каждой половине.
Разрез 3 дает 8 и 10.
Разрез 4 дает 9 и 9 помидоров на каждой половине.
Обратите внимание, что знание того, что всего 18 помидоров, позволяет нам проверить, что 9 помидоров находится только на одной половине.
Задание 15
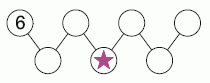
Маша хочет вписать числа 1, 2, 3, 4, 5, 6 и 7 в кружочки на рисунке. Каждое из чисел в нижнем ряду должно равняться сумме двух соседних чисел в верхнем ряду. Число 6 Маша уже вписала, как показано на рисунке. Какое число она должна вписать в кружок, отмеченный знаком  ?
?
A) 2 Б) 3 В) 4 Г) 5 Д) 7
Правильный ответ: В
Ответ участника: Б
Промежуточный результат: 33.25 - 1 = 32.25
1, 2, 3, 4, 5, 6, 7 — числа для заполнения. 6 уже есть. Под 6 сумма должна быть больше 6, так что это может быть только 7. 7 теперь находится в нижнем левом круге.
Нам нужно найти ответ для 6 + ... = 7, так что это может быть только 1.
Теперь у нас осталось 2, 3, 4, 5. Два самых больших числа должны быть суммами, так что идем в нижний ряд.
4 не может быть образовано путем суммирования пары из 2, 3 или 5. Поэтому 4 должно происходить из 1 + ... = 4. Это дает положение 4 внизу посередине, что является правильным ответом (звезда), а 3 — вверху. Затем 5 находится внизу справа, а 2 — вверху справа.
Задание 16
Борис складывает квадрат из 4-х прямоугольных частей. На рисунке показаны три из них. Какой из следующих частей может быть 4-я часть?

Правильный ответ: Д
Ответ участника: А
Промежуточный результат: 32.25 - 1 = 31.25
Наибольшая длина стороны одной из частей составляет 6 квадратов, поэтому большой квадрат имеет длину стороны не менее 6 квадратов. Поэтому большой квадрат состоит либо из 6×6 = 36, либо из 7×7 = 49 или ... квадратов.
Три данных части состоят из
8 + 10 + 6 = 24 маленьких квадратов в общей сложности. Таким образом, четвертая часть должна состоять либо из
36 − 24 = 12, либо из
49 − 24 = 25 или ... квадратов.
Ни одна из частей в вариантах не состоит из 25 или более квадратов. Таким образом, большой квадрат состоит из 36 квадратов и имеет длину стороны 6 квадратов. Чтобы найти правильную форму недостающей части, мы должны составить большой квадрат. Вторую часть нужно повернуть так же, как и первую. Недостающий прямоугольник имеет ширину 4 квадрата и высоту 3 квадрата, как показано на рисунке.

Таким образом, четвертая часть показана в варианте Д.
Задание 17
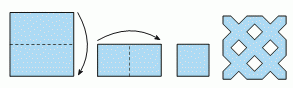
Нина сложила бумажный квадрат пополам, а затем ещё раз пополам, как показано на рисунке. Затем она отрезала кусочки от сложенной бумаги. Развернув, она получила бумажную снежинку, показанную на рисунке. Как она разрезала сложенный лист бумаги?
Правильный ответ: Б
Ответ участника: Г
Промежуточный результат: 31.25 - 1.25 = 30

Если добавить к снежинке две линии сгиба (как показано на рисунке), можно увидеть, что каждая четверть напоминает узор, показанный в варианте Б.
Задание 18
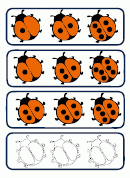
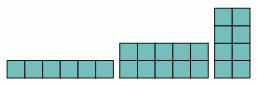
Марта сделала 4 фотографии. На каждой фотографии по 3 божьи коровки. Все божьи коровки изображены на фотографиях одинаковое количество раз. Три фотографии показаны на рисунке. Сколько всего точек на спине у трёх божьих коровок на четвёртой фотографии Марты?
A) 9 Б) 10 В) 11 Г) 12 Д) 23
Правильный ответ: Г
Ответ участника: Д
Промежуточный результат: 30 - 1.25 = 28.75
Каждая из божьих коровок с 1, 3 и 5 точками появляется дважды на первых трёх фотографиях, а те, у которых 2, 4, 6 точек, появляются один раз. Таким образом, на четвертой фотографии находятся божьи коровки с 2, 4 и 6 точками, всего 12 точек.
Задание 19
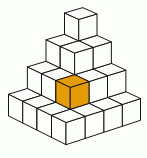
Лена построила пирамиду из оранжевых и белых кубиков. Никакие два кубика одинакового цвета не касаются гранями друг друга. Один из оранжевых кубиков показан на рисунке. Как выглядит пирамида Лены сверху?
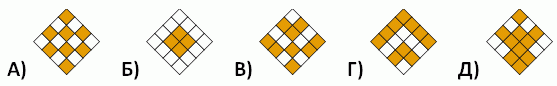
Правильный ответ: Г
Ответ участника: Г
Промежуточный результат: 28.75 + 5 = 33.75
Можно начать с размышлений о цвете куба, который находится прямо под оранжевым кубом — он должен быть белым. Значит, кубы X и Z, которые касаются этого белого куба в нижнем слое, должны быть оба оранжевыми, и, следовательно, куб Y должен быть белым.
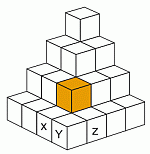
Единственный из пяти вариантов, который согласуется с известными кубиками, — это вариант Г. Рассматривая соседние с ними кубики, можно понять, что вариант Г действительно является правильным.
Альтернативное решение: В качестве первого шага мы раскрашиваем блоки так, чтобы блоки одного цвета не имели соприкасающихся граней. Есть только один вариант раскраски:
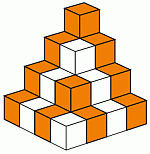
Если мы посмотрим на пирамиду сверху, мы увидим, что правильным решением является вариант Г.
Задание 20
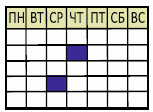
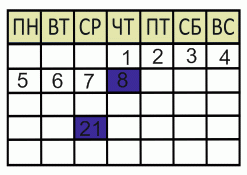
На рисунке показана страница одного месяца календаря без каких-либо дат. Сумма дат двух закрашенных дней равна 29. На какой день недели приходится первый день месяца?
A) Понедельник Б) Вторник В) Среда Г) Четверг Д) Воскресенье
Правильный ответ: Г
Ответ участника: В
Промежуточный результат: 33.75 - 1.25 = 32.5
Подсчитав количество дней от первого закрашенного квадрата до второго, мы видим, что вторая дата на 13 дней позже первой. Поэтому нам нужны два числа, которые отличаются на 13, а их сумма равна 29. Это числа 8 и 21. Первый день месяца находится ровно на одну неделю раньше 8-го дня, поэтому соответствующие дни недели совпадают, и это четверг.
Задание 21
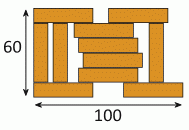
В конструкции на рисунке использовано 11 одинаковых кирпичей. Она имеет длину 100 см и ширину 60 см. Каковы размеры каждого кирпича?

Правильный ответ: Б
Ответ участника: В
Промежуточный результат: 32.5 - 1.25 = 31.25
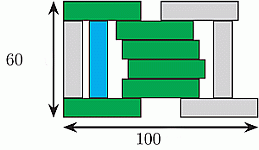
Смотря на 6 зеленых кирпичей, можно увидеть, что высота конструкции в 6 раз больше высоты каждого кирпича.
60 : 6 = 10, т.е. высота каждого кирпича составляет 10 см.
Обратим внимание на синий кирпич. Можно сделать вывод, что длина каждого кирпича в 4 раза больше его высоты. Поскольку 4 × 10 = 40, кирпич имеет длину 40 см.
Значит, размеры одного кирпича - 40 см × 10 см.
Мы не можем никак использовать данные о ширине конструкции, так как она не дает никакой информации из-за зазоров между кирпичами.
Задание 22
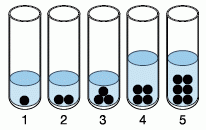
Одинаковые шарики поместили в 5 одинаковых пробирок, как показано на рисунке. Затем в каждую из этих пробирок была добавлена вода. Уровни воды в пробирках 1, 2 и 3 одинаковы. Уровни воды в пробирках 4 и 5 также одинаковы и в два раза выше, чем в первых 3 пробирках. Затем все шарики убрали из пробирок. В какой пробирке оказалось меньше всего воды?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
Правильный ответ: В
Ответ участника: А
Промежуточный результат: 31.25 - 1.25 = 30
Количество воды в пробирке 3 меньше, чем в 1 и 2, так как в ней больше шариков, а уровень воды одинаковый. Аналогично, количество воды в пробирке 5 меньше, чем в 4. Осталось сравнить пробирки 3 и 5. Если взять две пробирки 3 и вылить содержимое в одну, то получится содержимое пробирки 5. Таким образом, в пробирке 5 не только вдвое больше шариков, чем в пробирке 3, но и вдвое больше воды. Поэтому в пробирке 3 меньше всего воды.
Задание 23
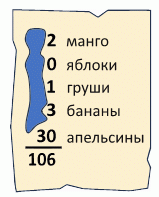
У Розы есть 106 фруктов пяти видов, более 10 фруктов каждого вида. Количество двух видов фруктов одинаково. Одного вида фруктов ровно в два раза больше, чем какого-то другого. Она записала их количества на бумаге, но первые цифры оказались замазаны. Сколько у Розы бананов?
A) 13 Б) 23 В) 43 Г) 53 Д) 63
Правильный ответ: А
Ответ участника: Г
Промежуточный результат: 30 - 1.25 = 28.75
Фрукты, количество которых одинаково, судя по последней цифре, это яблоки и апельсины, по 30 штук. Смотря на последние цифры, делаем вывод что фрукты, количество которых вдвое больше, это манго (*2) и груши (*1). Поскольку фруктов каждого вида более 10 штук, количество груш равно 11, или 21, или 31, или ..., а количество манго равно 22, или 42, или 62, или ... Манго, яблок, груш и апельсинов в сумме не менее
22 + 30 + 11 + 30 = 93.
Таким образом, бананов не более 106 - 93 = 13. Поскольку фруктов каждого вида более 10 штук, бананов 13.
Задание 24
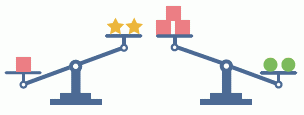
На двух весах показаны результаты взвешивания объектов трёх видов. Одинаковые объекты имеют одинаковые массы, разные объекты – разные массы. Масса одного объекта может равняться 1 кг, 2 кг, 3 кг, 4 кг или 5 кг. Какую массу имеет  ?
?
A) 1 кг Б) 2 кг В) 3 кг Г) 4 кг Д) 5 кг
Правильный ответ: В
Ответ участника: Д
Промежуточный результат: 28.75 - 1.25 = 27.5
Наименьшая возможная масса звезды составляет 1 кг.
Первое взвешивание показывает, что один квадрат тяжелее двух звезд. Из-за этого квадрат должен быть весом больше 2 кг; другими словами, 3 кг, 4 кг или 5 кг.
Второе взвешивание показывает, что два круга тяжелее трех квадратов. Три квадрата весят не менее 9 кг, что означает, что два круга должны весить не менее 9 кг. Мы знаем, что массы каждого из трех объектов составляют 1 кг, 2 кг, 3 кг, 4 кг или 5 кг, и поэтому один круг должен весить 5 кг.
Теперь масса одного квадрата может быть только 3 кг или 4 кг. Если один квадрат весит 4 кг, то три квадрата будут весить больше, чем 2 круга (так как 3 × 4 > 2 × 5), но это не то, что показано при взвешивании. Следовательно, масса одного квадрата должна быть 3 кг (а масса звезды — 1 кг).
Окончательный результат: 27.5
Место в Беларуси: 11826
Место в области: 1707
Место в районе: 240
Место в школе: 22
Участник получает свидетельство и "приз для всех".



