"Кенгуру-2024"

21 марта 2024
Задание для 9-10 классов

Участник: Мезько Ангелина, Языльская СШ , Стародорожский район

На старте каждый участник получает 30 баллов

Задание 1

Чему равно значение выражения

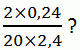
A) 0,01       Б) 0,1       В) 1       Г) 10       Д) 100

Правильный ответ: А

Ответ участника: А

Промежуточный результат: 30 + 3 = 33

Задание 2

Какой из следующих квадратов разрезан на две неравные части?

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 33 + 3 = 36

Задание 3

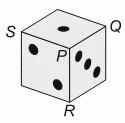
Число точек на противоположных гранях игрального кубика равно 7. Для каждой вершины вычислили сумму чисел точек на тех трёх гранях, которым принадлежит данная вершина. Например, для вершины P эта сумма равна

1 + 2 + 3 = 6.

Чему равна максимальная из сумм для вершин Q, R и S?

A) 7       Б) 9       В) 10       Г) 11       Д) 15

Правильный ответ: Г

Ответ участника: А

Промежуточный результат: 36 - 0.75 = 35.25

Задание 4

Игра «Прыжки по клеткам» проводится следующим образом. Каждый игрок прыгает в квадраты, чередуя прыжки: левая нога – обе ноги – правая нога – обе ноги – левая нога – обе ноги, и так далее, как показано на рисунке.

Майя сыграла в игру, начав с левой ноги, и закончила ровно на 48-й клетке. Сколько раз её левая нога коснулась земли?

A) 12       Б) 24       В) 36       Г) 49       Д) 48

Правильный ответ: В

Ответ участника: А

Промежуточный результат: 35.25 - 0.75 = 34.5

Задание 5

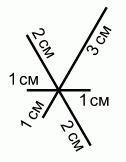
Тим хочет нарисовать несколько отрезков, показанных на рисунке, не отрывая карандаш от листа бумаги. Одни и те же линии можно повторять. Длины отрезков указаны на рисунке. Тим может начать рисовать с любой точки. Какое кратчайшее расстояние может пройти его карандаш, чтобы получить рисунок?

A) 14 см       Б) 15 см       В) 16 см       Г) 17 см       Д) 18 см

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 34.5 + 3 = 37.5

Задание 6

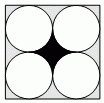
В квадрат вписаны четыре одинаковых круга так, как показано на рисунке. Как относится площадь чёрной части квадрата к площади его серой части?

A) 1 : 4

Б) 1 : 3

В) 2 : 3

Г) 3 : 4

Д) π : 4

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 37.5 - 0.75 = 36.75

Задание 7

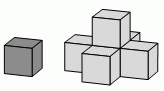
Джон строит на столе последовательно следующую конструкцию: сначала он ставит один кубик, затем добавляет к нему 5 таких же кубиков, чтобы закрыть все видимые грани данного кубика на столе. Какое наименьшее число кубиков ему нужно добавить на втором шаге, чтобы закрыть все видимые на столе грани конструкции, полученной на первом шаге?

A) 8       Б) 9       В) 10       Г) 13       Д) 19

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 36.75 + 3 = 39.75

Задание 8

Трёхзначный палиндром это – трёхзначное число вида aba, у которого первая и третья цифры совпадают, средняя цифра может быть любой. Какова сумма цифр наибольшего трёхзначного палиндрома, который делится на 6?

A) 16       Б) 18       В) 20       Г) 21       Д) 24

Правильный ответ: Д

Ответ участника: Б

Промежуточный результат: 39.75 - 0.75 = 39

Задание 9

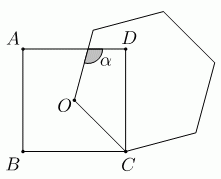
Мартин нарисовал квадрат ABCD и правильный шестиугольник со стороной OC, где O – центр данного квадрата. Чему равна величина угла α?

A) 105°       Б) 110°       В) 115°       Г) 120°       Д) 125°

Правильный ответ: А

Ответ участника: Г

Промежуточный результат: 39 - 0.75 = 38.25

Задание 10

Михаил окружил прямоугольное поле 40-метровым забором. Длины сторон поля выражаются целыми простыми числами метров. Какую максимальную площадь имеет данное поле?

A) 99 м²

Б) 96 м²

В) 91 м²

Г) 84 м²

Д) 51 м²

Правильный ответ: В

Ответ участника: Б

Промежуточный результат: 38.25 - 0.75 = 37.5

Задание 11

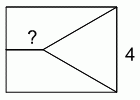
Прямоугольник разрезан на три части одинаковой площади, как показано на рисунке. Одна из частей – равносторонний треугольник со стороной 4 см, две другие – трапеции. Какова длина меньшей из параллельных сторон трапеций?

A) √2 см

Б) √3 см

В) 2√2 см

Г) 3 см

Д) 2√3 см

Правильный ответ: Б

Ответ участника: Г

Промежуточный результат: 37.5 - 1 = 36.5

Задание 12

Елена вписывает буквы А, В, С и D в таблицу 2 × 4, в каждую клетку ровно одну букву. Она хочет, чтобы в каждой строчке и в каждом квадрате 2 × 2 каждая из этих букв встречалась ровно один раз. Сколькими способами она может это сделать?

A) 12       Б) 24       В) 48       Г) 96       Д) 198

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 36.5 + 4 = 40.5

Задание 13

Дочь Марии сегодня родила девочку. Через два года произведение возрастов Марии, её дочери и её внучки будет равно 2024. Возраст Марии и её дочери – чётные числа. Сколько лет Марии сейчас?

A) 42       Б) 44       В) 46       Г) 48       Д) 50

Правильный ответ: Б

Ответ участника: Г

Промежуточный результат: 40.5 - 1 = 39.5

Задание 14

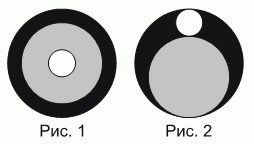
Сергей вырезал три круга из трёх кусков картона разного цвета. Он наложил круги друг на друга, как показано на рисунке 1. Затем он переместил круги так, чтобы их границы касались друг друга, как показано на рисунке 2. На первом рисунке площадь видимой чёрной области в 7 раз больше площади белого круга. Как относятся площади видимых чёрных областей на первом и втором рисунках?

A) 3 : 1

Б) 4 : 3

В) 6 : 5

Г) 7 : 6

Д) 9 : 7

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 39.5 - 1 = 38.5

Задание 15

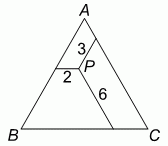
Из точки P внутри равностороннего треугольника проведены три отрезка параллельно его сторонам, как показано на рисунке. Длины этих отрезков равны 2 м, 3 м и 6 м. Чему равен периметр данного треугольника?

A) 22 м       Б) 26 м       В) 33 м       Г) 39 м       Д) 44 м

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 38.5 + 4 = 42.5

Задание 16

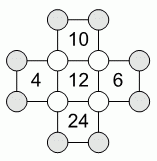
В каждом из двенадцати кружочков на рисунке вписано число. Внутри каждого квадрата указано произведение чисел в его четырёх вершинах. Чему равно произведение чисел в восьми серых кружочках?

A) 20       Б) 40       В) 80       Г) 120       Д) 480

Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 42.5 - 1 = 41.5

Задание 17

В четырёх вазах лежат конфеты. Число конфет в первой вазе равно числу ваз, в которых лежит ровно 1 конфета. Число конфет во второй вазе равно числу ваз, в которых лежат ровно 2 конфеты. Число конфет в третьей вазе равно числу ваз, в которых лежат ровно 3 конфеты. Число конфет в четвёртой вазе равно числу ваз, в которых нет ни одной конфеты. Сколько всего конфет лежат во всех вазах?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

Правильный ответ: В

Ответ участника: Д

Промежуточный результат: 41.5 - 1 = 40.5

Задание 18

У Жана-Филиппа есть n³ (n > 2) одинаковых кубиков. Он построил из них большой куб и покрасил всю его внешнюю поверхность. Оказалось, что количество кубиков, у которых окрашена ровно одна грань, равно количеству кубиков, у которых не окрашена ни одна грань. Какое значение имеет n?

A) 4       Б) 6       В) 7       Г) 8       Д) 10

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 40.5 + 4 = 44.5

Задание 19

У Кристины есть набор карточек с номерами от 1 до 12. Она разложила восемь из них по кругу так, что сумма номеров на любых двух соседних карточках делится на 3. Какие карточки оказались не использованы?

A) 1, 2, 9, 12

Б) 3, 5, 7, 9

В) 1, 2, 11, 12

Г) 5, 6, 7, 8

Д) 3, 6, 9, 12

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 44.5 + 4 = 48.5

Задание 20

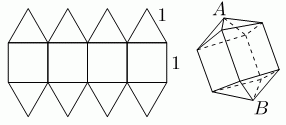
Поверхность многогранника состоит из квадратов со стороной 1 и равносторонних треугольников со стороной 1. Чему равно расстояние между вершинами А и В?

A) √5

Б) 1 + √2

В) 2,5

Г) 1 + √3

Д) 2√2

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 48.5 + 4 = 52.5

Задание 21

Евгений представил число

n! = 1 • 2 • . . . • n

в виде произведения степеней различных простых чисел. Но часть его записи оказалась залита чернилами. Простые числа в этой записи расположены в порядке возрастания. Какую степень в этом произведении имеет число 17?

A) 1       Б) 2       В) 3       Г) 4       Д) 5

Правильный ответ: В

Ответ участника: Б

Промежуточный результат: 52.5 - 1.25 = 51.25

Задание 22

Карл всегда говорит правду или всегда лжёт в разные дни. Однажды он сделал ровно четыре из следующих пяти утверждений. Какое из следующих утверждений он не мог сделать в этот день?

A) Я солгал вчера и буду лгать завтра.

Б) Сегодня я говорю правду и буду говорить правду завтра.

В) Число 2024 делится на 11.

Г) Вчера была среда.

Д) Завтра будет суббота.

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 51.25 + 5 = 56.25

Задание 23

Сумма цифр числа N в три раза больше суммы цифр числа N + 1. Какое наименьшее значение может иметь сумма цифр числа N?

A) 9       Б) 12       В) 15       Г) 18       Д) 27

Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 56.25 - 1.25 = 55

Задание 24

У Юли есть несколько чёрных, серых и белых единичных кубиков. Она строит куб 3 × 3 × 3 из 27 кубиков. Юля хочет, чтобы поверхность этого куба была ровно на одну треть чёрной, на одну треть серой и на одну треть белой. Пусть наименьшее возможное количество чёрных кубиков, которые ей понадобятся, равно А, а наибольшее – равно B. Чему равна разность B − A?

A) 1       Б) 3       В) 6       Г) 7       Д) 9

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 55 + 5 = 60

Задание 25

Аня подбросила игральный кубик 24 раза. Все числа от 1 до 6 выпали хотя бы один раз. Число 1 выпало больше раз, чем любое другое число. Аня сложила все выпавшие числа. Какое наибольшее значение может иметь сумма всех выпавших чисел?

A) 83       Б) 84       В) 89       Г) 90       Д) 100

Правильный ответ: Г

Ответ участника: А

Промежуточный результат: 60 - 1.25 = 58.75

Задание 26

Оля гуляла в парке. Половину времени она шла со скоростью 2 км/ч. Половину всего пройденного пути она шла со скоростью 3 км/ч. Остальное время она шла со скоростью 4 км/ч. Какую часть от всего времени прогулки она шла со скоростью 4 км/ч?

A) 1/14       Б) 1/12       В) 1/7       Г) 1/5       Д) 1/4

Правильный ответ: А

Ответ участника: Д

Промежуточный результат: 58.75 - 1.25 = 57.5

Задание 27

Алла выписала все натуральные числа от 1 до 25. Она хочет стереть некоторые из них так, чтобы оставшиеся числа можно было разбить на две группы с одинаковыми произведениями чисел в этих группах. Какое наименьшее количество чисел Алла может стереть?

A) 4       Б) 5       В) 6       Г) 7       Д) 8

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 57.5 + 5 = 62.5

Задание 28

Дэвид соединил всевозможными отрезками вершины правильного 20-угольника. Сколько из этих отрезков длиннее радиуса описанной окружности данного 20-угольника, но меньше её диаметра?

A) 90       Б) 100       В) 120       Г) 140       Д) 160

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 62.5 + 5 = 67.5

Задание 29

На плоскости проведено n различных прямых, обозначенных ℓ₁, ℓ₂, ... , ℓ_n. Прямая ℓ₁ пересекает ровно 5 других прямых, прямая ℓ₂ пересекает ровно 9 других прямых, а прямая ℓ₃ пересекает ровно 11 других прямых. Какое из чисел является наименьшим возможным значением n?

A) 11       Б) 12       В) 13       Г) 14       Д) 15

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 67.5 - 1.25 = 66.25

Задание 30

Пусть m и n – целые числа,

0 < m < n,

и пусть P(m; n), Q(n; m) и O(0; 0) – точки на координатной плоскости.

Сколько существует пар (m, n), таких, что площадь треугольника OPQ равна 2024?

A) 4       Б) 6       В) 8       Г) 10       Д) 12

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 66.25 + 5 = 71.25

Окончательный результат: 71.25

Место в Беларуси: 369

Место в области: 72

Место в районе: 2

Место в школе: 1

Участник получает свидетельство, "приз для всех" и приз за высокий результат.