"Кенгуру-2024"

21 марта 2024
Задание для 5-6 классов

Участник: Зеленко Мила, Языльская СШ , Стародорожский район

На старте каждый участник получает 30 баллов

Задание 1

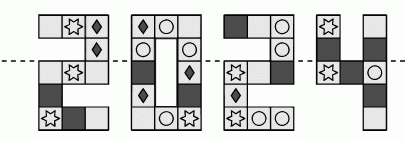
Алина согнула бумагу с рисунком по пунктирной линии. Какой из квадратов наложился на квадрат с таким же изображением?

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 30 + 3 = 33

Задание 2

В игре «Прыжки по клеткам» каждый игрок прыгает в квадраты, чередуя прыжки: обе ноги – левая нога – обе ноги – правая нога – обе ноги – левая нога и так далее, как показано на рисунке.

Маша начинает игру с прыжка в клетку «обе ноги». На каком прыжке Маша приземлится только на правую ногу?

A) на 10-м

Б) на 15-м

В) на 20-м

Г) на 22-м

Д) на 23-м

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 33 + 3 = 36

Задание 3

Саша изобрёл секретный алфавит. На нём слова BASIL и RED запишутся как

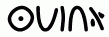и .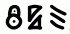

Как в этом алфавите запишется слово BREAD?

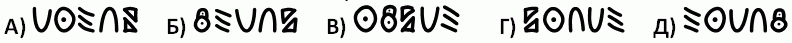
Правильный ответ: В

Ответ участника: В

Промежуточный результат: 36 + 3 = 39

Задание 4

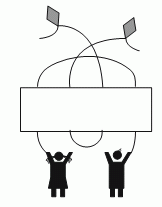
Какую из полосок следует разместить в середине рисунка сверху, чтобы от каждого ребёнка нити шли к разным воздушным змеям?

Правильный ответ: Г

Ответ участника: Г

Промежуточный результат: 39 + 3 = 42

Задание 5

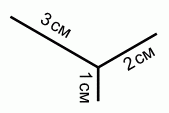
Маша хочет нарисовать линии на рисунке, не отрывая карандаш от бумаги. Какова длина самого короткого пути, который должен пройти карандаш?

A) 6 см       Б) 7 см       В) 8 см       Г) 9 см       Д) 10 см

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 42 + 3 = 45

Задание 6

Дина поставила три столбика на пол за ширмой. Если смотреть на них спереди, то вид будет такой, как на рисунке.

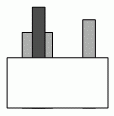
Каким будет вид на столбики сзади?

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 45 + 3 = 48

Задание 7

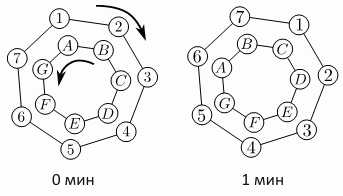
Даны 2 колеса, каждое из которых имеет 7 позиций. Колёса вращаются в противоположных направлениях, и каждое делает полный оборот за 7 минут. Через каждую минуту каждая буква находится рядом с некоторым числом. На рисунке показаны первые два положения колёс. Мы видим, что вначале буква А находится рядом с числом 1, буква В – рядом с числом 2 и так далее. Колёса вращаются до тех пор, пока буква C не окажется рядом с числом 2. Какое число будет рядом с буквой F?

A) 1       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 48 + 3 = 51

Задание 8

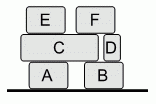
В грузовике находятся 6 коробок. Рабочий разгружает их на землю. Он берёт по одной коробке из грузовика при условии, что сверху у неё нет других коробок, и кладёт её на землю или на другую уже взятую ранее коробку. Какая из стопок у него не могла получиться после полной разгрузки?

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 51 + 3 = 54

Задание 9

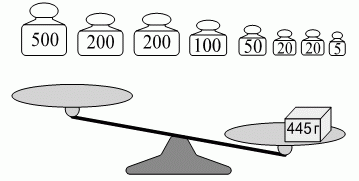
У Пети есть пакет весом 445 г и восемь гирь (с маркировкой в граммах). Он положил пакет на чашу весов. Какое наименьшее количество гирь ему после этого нужно положить на чаши, чтобы их уравновесить?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

Правильный ответ: Б

Ответ участника: Г

Промежуточный результат: 54 - 0.75 = 53.25

Задание 10

Комнаты в гостинице пронумерованы по порядку без пропусков, начиная с 1. Известно, что цифра 2 в номерах комнат встречается 14 раз, а цифра 5 встречается 3 раза. Какое наибольшее количество номеров может быть в этой гостинице?

A) 25       Б) 26       В) 34       Г) 35       Д) 41

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 53.25 + 3 = 56.25

Задание 11

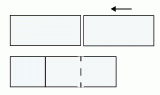
Два одинаковых прямоугольника площадью 18 склеили так, что получился прямоугольник, который можно разрезать на 3 одинаковых квадрата. Какую площадь имеет склеенный прямоугольник?

A) 24       Б) 27       В) 30       Г) 32       Д) 36

Правильный ответ: Б

Ответ участника: Г

Промежуточный результат: 56.25 - 1 = 55.25

Задание 12

У Дениса есть пять коробок шоколадных конфет с этикетками A, B, C, D и E. В каждой коробке по 5 конфет. Конфетам присвоены номера в зависимости от их вкуса, как показано на рисунке.

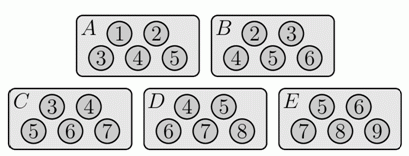
Денис съел большую часть конфет. На рисунке ниже показано, что осталось в коробках.

Какая этикетка на коробке Х?

A) A       Б) B       В) С       Г) D       Д) E

Правильный ответ: Д

Ответ участника: А

Промежуточный результат: 55.25 - 1 = 54.25

Задание 13

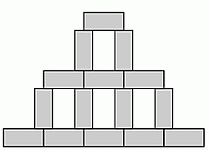
Роза разложила на столе несколько одинаковых прямоугольных плиток так, что получилась конструкция, показанная на рисунке. Ширина конструкции равна 45 см, а высота – 30 см. Чему равна площадь одной плитки?

A) 24 см²

Б) 27 см²

В) 30 см²

Г) 33 см²

Д) 36 см²

Правильный ответ: Д

Ответ участника: Д

Промежуточный результат: 54.25 + 4 = 58.25

Задание 14

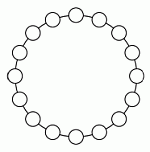
В каждом из 16 кружочков записано число. Числа в соседних кружочках отличаются на 1. В одном из кружочков записано число 5, а в другом – число 13. Сколько различных чисел записано во всех 16 кружочках?

A) 9       Б) 10       В) 13       Г) 14       Д) 16

Правильный ответ: А

Ответ участника: Г

Промежуточный результат: 58.25 - 1 = 57.25

Задание 15

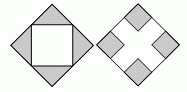
На рисунке изображены два квадрата одинаковой площади с серыми и белыми частями. В первом квадрате белая часть – квадрат с вершинами в серединах сторон исходного квадрата. Во втором квадрате стороны четырёх серых квадратов составляют одну треть от стороны исходного квадрата. Площадь серой части первого квадрата равна 9. Какова площадь серой части второго квадрата?

A) 6       Б) 8       В) 9       Г) 10       Д) 12

Правильный ответ: Б

Ответ участника: А

Промежуточный результат: 57.25 - 1 = 56.25

Задание 16

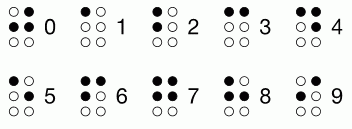
Десятичные цифры в системе Брайля для слепых представлены наборами чёрных и белых точек, как показано на рисунке. Сколько различных двузначных чисел содержат ровно пять чёрных точек?

A) 16       Б) 18       В) 30       Г) 32       Д) 34

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 56.25 + 4 = 60.25

Задание 17

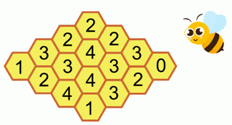
Пчелиные соты на рисунке состоят из 16 ячеек. В некоторых ячейках есть мёд. Число в каждой ячейке указывает, сколько соседних по стороне ячеек содержат мёд. Сколько всего ячеек в сотах содержат мёд?

A) 7       Б) 8       В) 9       Г) 10       Д) 11

Правильный ответ: В

Ответ участника: А

Промежуточный результат: 60.25 - 1 = 59.25

Задание 18

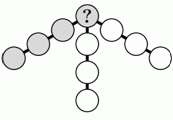
Аня вписывает числа от 1 до 10 в кружочки на диаграмме (каждое ровно один раз, в каждый кружочек ровно одно число). Аня хочет, чтобы в каждой четвёрке кружочков, расположенных на одной прямой (например, в серых кружочках) сумма чисел равнялась 23. Какое число она должна вписать в кружочек со знаком вопроса?

A) 4       Б) 5       В) 6       Г) 7       Д) 8

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 59.25 - 1 = 58.25

Задание 19

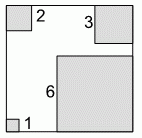
Кристиан вырезал из углов большого квадрата четыре меньших квадрата, как показано на рисунке. Площадь оставшейся части квадрата оказалась равна половине его всей площади. Длины сторон вырезанных квадратов указаны на рисунке. Чему равен периметр оставшейся части большого квадрата?

A) 36       Б) 40       В) 44       Г) 48       Д) 52

Правильный ответ: Б

Ответ участника: Б

Промежуточный результат: 58.25 + 4 = 62.25

Задание 20

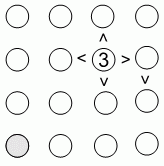
Рита решает головоломку. Она хочет вписать числа 1, 2, 3 и 4 в кружочки на рисунке так, чтобы в каждой строке и каждом столбце каждое из этих чисел встречалось ровно один раз. При этом, одно число – число 3 – уже вписано так, как показано на рисунке. Оно должно быть больше всех четырёх соседних чисел. Кроме того, в правом столбце второе сверху число должно быть больше третьего. Какое число Рита должна вписать в серый кружочек?

A) 1       Б) 2       В) 3       Г) 4       Д) 2 или 3

Правильный ответ: А

Ответ участника: В

Промежуточный результат: 62.25 - 1 = 61.25

Задание 21

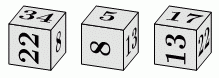
На рисунке изображены три одинаковых специальных кубика. Чему равна сумма чисел на их нижних гранях?

A) 26       Б) 40       В) 43       Г) 47       Д) 56

Правильный ответ: В

Ответ участника: В

Промежуточный результат: 61.25 + 5 = 66.25

Задание 22

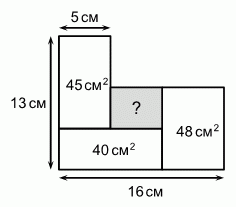
На рисунке изображены четыре соприкасающихся прямоугольника. Площади трёх из них указаны. Чему равна площадь серого прямоугольника?

A) 12 см²

Б) 14 см²

В) 16 см²

Г) 18 см²

Д) 20 см²

Правильный ответ: Д

Ответ участника: В

Промежуточный результат: 66.25 - 1.25 = 65

Задание 23

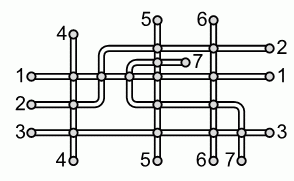
На рисунке показан план семи трамвайных линий небольшого города. Кружочки обозначают остановки. Мартин хочет раскрасить линии так, чтобы пересекающиеся на остановках линии были окрашены в разные цвета. Какое наименьшее количество разных цветов ему понадобится?

A) 3       Б) 4       В) 5       Г) 6       Д) 7

Правильный ответ: А

Ответ участника: Д

Промежуточный результат: 65 - 1.25 = 63.75

Задание 24

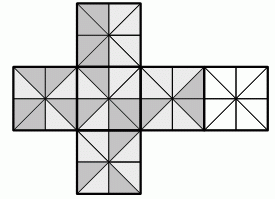
Дима сворачивает куб из указанной на рисунке развёртки. Он хочет, чтобы соприкасающиеся треугольники на соседних по ребру гранях были окрашены одинаково. Как для этого ему следует окрасить треугольники правого неокрашенного квадрата?

Правильный ответ: Б

Ответ участника: В

Промежуточный результат: 63.75 - 1.25 = 62.5

Задание 25

Света достаёт из буфета четыре кружки и расставляет их случайным образом на четыре блюдца. Какое из следующих утверждений является заведомо верным?

A) Ни одна из четырёх кружек не стоит на соответствующем ей блюдце.

Б) На соответствующем блюдце стоит ровно 1 кружка.

В) Не могут на соответствующих блюдцах стоять ровно 2 кружки.

Г) Не могут на соответствующих блюдцах стоять ровно 3 кружки.

Д) Не могут все 4 кружки стоять на соответствующих блюдцах.

Правильный ответ: Г

Ответ участника: Б

Промежуточный результат: 62.5 - 1.25 = 61.25

Задание 26

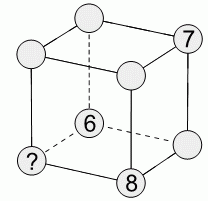
Мария хочет вписать числа от 1 до 8 в вершины куба так, чтобы суммы чисел в вершинах каждой грани были одинаковы. Числа 6, 7 и 8 Мария уже вписала так, как показано на рисунке. Какое число она должна вписать в вершину, обозначенную знаком вопроса?

A) 1       Б) 2       В) 3       Г) 4       Д) 5

Правильный ответ: В

Ответ участника: Д

Промежуточный результат: 61.25 - 1.25 = 60

Задание 27

У бабушки есть много конфет. Она решила раздать их своим внукам так, чтобы все получили как можно больше конфет, но поровну. Когда все внуки получили по 20 конфет, у бабушки осталось 12 конфет, и она не смогла продолжить раздачу так, чтобы все внуки получили конфет поровну. Какое наименьшее количество конфет могло быть у бабушки?

A) 52       Б) 232       В) 272       Г) 411       Д) 432

Правильный ответ: В

Ответ участника: Б

Промежуточный результат: 60 - 1.25 = 58.75

Задание 28

Дима хочет разрезать верёвку на 12 равных частей и отмечает на ней точки разреза. Миша хочет разрезать эту же веревку на 16 равных частей и также отмечает на ней соответствующие точки разреза. После этого Майя разрезает верёвку во всех отмеченных точках. Сколько кусков верёвки получилось?

A) 24       Б) 25       В) 27       Г) 28       Д) 29

Правильный ответ: А

Ответ участника: Г

Промежуточный результат: 58.75 - 1.25 = 57.5

Задание 29

Эмма играет с семью фрагментами пазла, показанными на рисунке Она хочет построить гусеницу, у которой есть одна голова, один хвост и один, два или три фрагмента между ними. Сколько разных гусениц Эмма может построить?

A) 10       Б) 14       В) 16       Г) 18       Д) 20

Правильный ответ: Д

Ответ участника: А

Промежуточный результат: 57.5 - 1.25 = 56.25

Задание 30

Ева записала на доске трёхзначное число. Затем Брэндон приписал к нему четвёртую цифру справа. В результате число увеличилось на 2024. Какую цифру приписал Брэндон?

A) 2       Б) 3       В) 4       Г) 8       Д) 9

Правильный ответ: Г

Ответ участника: В

Промежуточный результат: 56.25 - 1.25 = 55

Окончательный результат: 55

Место в Беларуси: 2264

Место в области: 462

Место в районе: 8

Место в школе: 2

Участник получает свидетельство и "приз для всех".