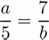Задание 1
|
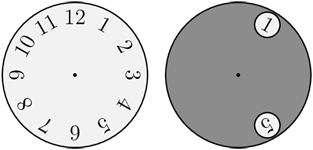
Серым кругом с двумя отверстиями накрыли циферблат таких же размеров, как показано на рисунке. Круг повернули вокруг центра так, что в одном из отверстий оказалась число 10. Какие из следующих чисел можно увидеть в другом отверстии?
A) 2 или 6
Б) 3 или 7
В) 3 или 6
Г) 1 или 9
Д) 2 или 7
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
На рисунке в условии задачи видно, что разница между числами в отверстиях серого круга равна 4. Ясно, что это условие сохраняется при поворотах данного круга (с соответствующей поправкой, если после поворота в одном отверстии оказалось число 12 или перешло через него). Поэтому, если в одном из отверстий оказалось число 8, то в другом будет либо 10 – 4 = 6, либо 10 + 4 = 14, т. е., с учётом поправки, 14 – 12 = 2.
|
Задание 2
|
Марии пришлось бежать, чтобы сесть в вагон метро. Затем она проехала две остановки и пошла в школу пешком. Какой из следующих графиков скорость-время лучше всего представляет ее путешествие?

|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
По условию, на графике должны быть пять точек на оси t, в которых скорость Марии нулевая: это момент начала движения, момент посадки Марии в стоящий поезд метро, момент первой остановки, момент второй остановки, когда Мария вышла из поезда, и, наконец, момент, когда Мария пришла к пункту назначения (скажем, в школу). Такому свойству удовлетворяют графики Б и Г. Но ответ Б противоречит действительности – из него бы следовало, что Мария бежала быстрее поезда метро. Поэтому правильный ответ Г.
|
Задание 3
|
Натуральные числа m и n - нечётные. Какое из следующих целых чисел также нечётное?
A) m(n + 1)
Б) (m + 1)(n + 1)
В) m + n + 2
Г) m(n + 2)
Д) m + n
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Согласно условию, число n + 1 чётное. Поэтому произведения
А) m(n + 1) и Б) (m + 1)(n + 1)
чётные.
Сумма двух нечётных чисел является чётной. Поэтому числа
Д) m + n и В) m + n + 2 также чётные.
В ответе Г) m(n + 2) мы имеем произведение двух нечётных чисел. Поэтому оно нечётно. Видим, что правильным является ответ Г.
|
Задание 4
|
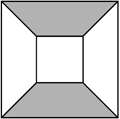
В большом квадрате со стороной 10 см находится меньший квадрат со стороной 4 см, как показано на рисунке. Соответствующие стороны этих квадратов параллельны. Сколько процентов (по площади) большого квадрата составляет его серая часть?
A) 25% Б) 30% В) 40% Г) 42% Д) 45%
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Согласно условию, серая часть квадрата – это две трапеции. Их основания равны 10 и 4 см, а сумма высот равна 10 – 4 = 6 см. Поэтому их суммарная площадь равна
(10 + 4)/ 2 ⋅ 6 = 42 см2.
Это составляет 42% от площади
большого квадрата, равной 100 см2.
|
Задание 5
|
Сегодня четверг. Какой день недели будет через 2023 дня?
A) вторник Б) среда В) четверг Г) пятница Д) суббота
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Поскольку в неделе 7 дней и 2023 = 7 · 289 – делится на 7, то через 2023 дня после четверга снова будет четверг.
|
Задание 6
|

Прямоугольник на рисунке разбит на 30 равных квадратных клеток. Периметр заштрихованной области равен 240 см. Чему равна площадь данного прямоугольника?
A) 480 см2
Б) 750 см2
В) 1080 см2
Г) 1920 см2
Д) 2430 см2
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Заштрихованная область имеет на 4 вертикальные стороны и на 4 горизонтальные стороны клеточек больше, чем прямоугольник, поэтому её периметр равен
2 · (5 + 6) + 4 + 4 = 30 сторон клеточек.
Поэтому сторона одной клетки равна
240 : 30 = 8 см.
Тогда площадь данного прямоугольника равна
30 · 82 = 1920 см2.
|
Задание 7
|
Возраст семьи из пяти человек в сумме составляет 80 лет. Двум младшим детям 6 и 8 лет. Сколько лет в сумме было членам этой семьи семь лет назад?
A) 35 Б) 36 В) 45 Г) 46 Д) 66
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Семь лет назад самого младшего, которому сейчас 6 лет, ещё не было. Поэтому в семье было четверо человек, и 7 лет назад им было
(80 – 6) – 4 · 7 = 74 – 28 = 46 лет.
|
Задание 8
|
Деревянный забор состоит из ряда вертикальных и горизонтальных досок. Первая и последняя доски в заборе вертикальные. Любые две соседние вертикальные доски соединены четырьмя горизонтальными. Каким из следующих чисел может быть общее число досок в заборе?
A) 95 Б) 96 В) 97 Г) 98 Д) 99
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Первая часть забора состоит из 6 досок (2 вертикальные и 4 горизонтальные). Каждая следующая часть состоит из 5 досок (ещё 4 горизонтальные доски и 1 вертикальная). Поэтому число досок в заборе имеет вид
5n + 1, где n – некоторое натуральное число.
Из предлагаемых вариантов ответа остаток 1 при делении на 5 имеет
только число 96.
|
Задание 9
|
Буквы a и b в уравнении
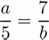
нужно заменить натуральными числами так, чтобы это уравнение превратилось в правильное равенство. Сколькими способами это можно сделать?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Уравнение в условии задачи равносильно
a · b = 5 · 7 = 35.
Существует ровно 4 способа, как (с учётом порядка множителей) число 35 можно представить в виде произведения двух натуральных чисел:
35 = 1 · 35 = 5 · 7 = 7 · 5 = 35 · 1.
|
Задание 10
|
После того, как я сыграл 200 партий в шахматы, количество моих побед составляет ровно 49%. Какое наименьшее количество дополнительных партий мне нужно сыграть, чтобы увеличить процент выигрышей ровно до 50% (при условии, что все дополнительные партии будут выиграны)?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Победа в 49% из 200 игр означает победу в 200 · 0,49 = 98 партиях и не победу в 200 – 98 = 102 партиях.
Чтобы уравнять число побед и не побед, необходимо выиграть ещё 102 – 98 = 4 партии. Поэтому правильным является ответ 4.
|
Задание 11
|
Дженни пытается экономить воду. Она сократила время, проводимое в душе, на четверть. Она также снизила напор воды в душе, чтобы на четверть уменьшить объём вытекающей воды за единицу времени. На какую часть Дженни уменьшила общее количество потребляемой воды?
A) на 1/4
Б) на 3/8
В) на 5/8
Г) на 5/12
Д) на 7/16
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Согласно условию, объём воды, используемой Дженни, стал равен
3/4 · 3/4 = 9/16 от первоначального.
Поэтому она уменьшила объём потребляемой воды на
1 - 9/16 = 7/16
|
Задание 12
|
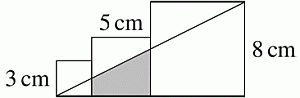
На рисунке показаны три квадрата со сторонами 3 см, 5 см и 8 см. Чему равна площадь серой трапеции?
A) 13 см2
Б) 55/4 см2
В) 61/4 см2
Г) 65/4 см2
Д) 69/4 см2
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть a и b – вертикальные стороны серой трапеции (в см). Из подобия имеющихся на рисунке прямоугольных треугольников следует
a/3 = b/(3 + 5) = 8/(3 + 5 + 8),
откуда a = 1,5 (см) и b = 4 (см).
Тогда площадь серой трапеции равна
(1,5 + 4)/2 · 5 = 55/4 (см2)
|
Задание 13
|
Проволоку длиной 95 м разрезали на три куска так, чтобы каждый следующий кусок был на 50% длиннее предыдущего. Какова длина самого длинного куска?
A) 36 м Б) 42 м В) 45 м Г) 46 м Д) 48 м
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть длина самого короткого куска равна x м. Тогда следующие два куска имеют длину 1,5x (м) и 1,5 · 1,5x = 2,25x (м). Согласно условию,
x + 1,5x + 2,25x = 95, или
4,75x = 95, откуда x = 20 (м). Тогда длина самого длинного куска равна
2,25 · 20 = 45 (м).
|
Задание 14
|
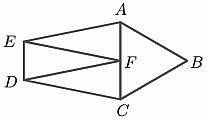
Пятиугольник ABCDE разбит на четыре треугольника с равными периметрами. Треугольник ABC равносторонний, а треугольники AEF, DFE и CDF — равные равнобедренные. Как относится периметр пятиугольника ABCDE к периметру треугольника ABC?
A) 2 : 1
Б) 3 : 2
В) 4 : 3
Г) 5 : 3
Д) 5 : 2
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть сторона равностороннего треугольника равна 2а. Тогда его периметр равен 6а, а стороны других треугольников такие, как показаны на рисунке.
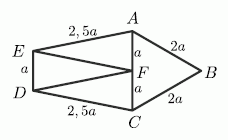
Поэтому периметр данного пятиугольника равен
a + 2,5a + 2,5a + 2a + 2a = 10a.
Его отношение к периметру равностороннего треугольника равно
10a : 6a = 5 : 3.
|
Задание 15
|
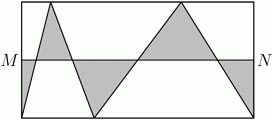
Точки M и N ─ середины двух сторон прямоугольника (см. рис.). Какая часть площади прямоугольника закрашена?
A) 1/6 Б) 1/5 В) 1/4 Г) 1/3 Д) 1/2
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть основание прямоугольника равно а, а высота равна h. Тогда площадь прямоугольника равна ah. Все закрашенные треугольники имеют высоту h/2, а сумма длин их оснований равна а. Поэтому площадь серой части данного прямоугольника равна
а/2 ⋅ h/2 = ah/4, что составляет 1/4 часть площади этого прямоугольника.
|
Задание 16
|
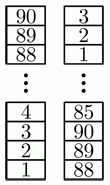
На столе стоит башня, состоящая из блоков, пронумерованных числами от 1 до 90 снизу вверх. Боря строит новую башню следующим образом. Он берёт три блока с вершины исходной башни и кладёт их на стол в качестве основания новой башни. Затем он берёт следующие три верхних блока из оставшейся части исходной башни и кладёт их на вершину новой башни, как показано на рисунке, и т. д. Сколько блоков будет между блоками 39 и 40 в новой башне?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
В новой башне под каждым блоком, пронумерованным целым числом, кратным 3, будет ниже блок с номером, меньшим на 1, ещё ниже – блок с номером, меньшим на 2. Число 39 делится на 3. Поэтому под ним будут блоки с номерами 38 и 37. Далее, под блоком номер 37 будет блок номер 42 (следующим за 39 числом, кратным 3). Под ним будут блоки 41 и 40. Видим, что между блоками 39 и 40 будет 4 блока (38, 37, 42 и 41).
|
Задание 17
|
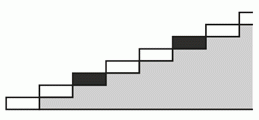
Каждая третья ступенька лестницы с 2023 ступеньками окрашена в чёрный цвет. Начало лестницы показано на рисунке. Аня поднимается по ступенькам по одной, начиная с правой или левой ноги, чередуя шаги левой и правой ногой. Какое наименьшее число чёрных ступеней она может пройти правой ногой?
A) 0 Б) 333 В) 336 Г) 337 Д) 674
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Независимо от того, начинает ли Аня с правой или с левой ноги, каждые 6 шагов будут повторяться. При этом за эти 6 шагов она наступает ровно на одну чёрную ступеньку правой ногой и на одну чёрную ступеньку левой ногой. Поскольку
2023 = 337 · 6 + 1
и первый шаг в каждой шестёрке шагов приходится на белую ступеньку, правой ногой Аня пройдёт 337 чёрных ступенек.
|
Задание 18
|
Будем называть двузначное число бесстепенным, если ни одна из его цифр не может быть записана как целое число в степени, большей 1. Например, число 53 является бесстепенным, а число 54 не является бесстепенным, поскольку 4 = 22. Какое из следующих чисел является общим делителем наименьшего и наибольшего двузначных бесстепенных чисел?
A) 3 Б) 5 В) 72 Г) 11 Д) 13
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Согласно условию, цифрами бесстепенного числа могут быть только цифры 2, 3, 5, 6 и 7. Поэтому самое маленькое бесстепенное число равно 22, а самое большое из них – 77. Общими делителями чисел 22 и 77
являются только числа 1 и 11. Из предлагаемых вариантов ответа подходит только ответ 11.
|
Задание 19
|
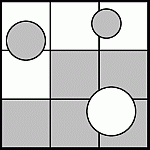
Квадрат со стороной 30 см разбит на 9 одинаковых меньших квадратов. В исходном квадрате находятся 3 круга: радиуса 5 см (внизу справа), 4 см (вверху слева) и 3 см (вверху справа), как показано на рисунке. Чему равна площадь серой части исходного квадрата?
A) 400 см2
Б) 500 см2
В) (400+50π) см2
Г) (500-25π) см2
Д) (500+25π) см2
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Заметим, что площадь белого круга 25π равна сумме площадей двух серых кругов 16π + 9π. Поэтому площадь серой части не изменится, если у серых и белого круга поменять окраску на противоположную. При этом получим 5 серых клеток из 9 клеток. Так как сторона одной клетки равна
30 : 3 = 10 (см),
площадь пяти клеток равна
5 · 10 · 10 = 500 см2.
|
Задание 20
|
Тима вычисляет среднее арифметическое значение пяти различных простых чисел. Какое наименьшее ЦЕЛОЕ значение он может получить?
A) 2 Б) 5 В) 6 Г) 12 Д) 30
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Наименьшая сумма первых 5 различных простых чисел
2 + 3 + 5 + 7 + 11 = 28
не делится на 5.
Следующая по величине сумма пяти простых чисел равна
2 + 3 + 5 + 7 + 13 = 30.
Среднее арифметической этих чисел равно
30 : 5 = 6.
|
Задание 21
|
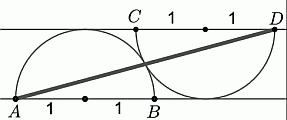
На рисунке показаны две соприкасающиеся полуокружности радиуса 1 с параллельными диаметрами АВ и CD. Чему равен квадрат длины отрезка AD?
A) 16
Б) 8 + 4√3
В) 12
Г) 9
Д) 5 + 2√3
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть О1 и О2 – центры данных полуокружностей. Проведём перпендикуляр О2E к прямым, на которых находятся диаметры данных полуокружностей (см. рис.).
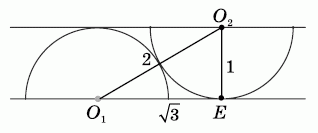
Тогда в прямоугольном треугольнике О1О2Е имеем:
О1О2 = 1 + 1 = 2 и О2E = 1,
откуда, по теореме Пифагора,
О1E = √3.
Проведём ещё один перпендикуляр DF к рассматриваемым прямым.
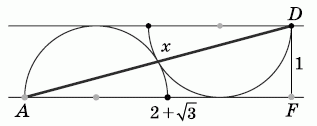
В образовавшемся прямоугольном треугольнике ADF имеем:
AF = 1 + √3 + 1 = 2 + √3 и DF = 1.
Тогда, по теореме Пифагора,
AD2 = (2 + √3)2 + 12 = 8 + 4√3.
|
Задание 22
|
Машина «Кенгуру» выполняет следующие операции. Если в машину введены 4 неотрицательных целых числа, она дописывает к ним наименьшее неотрицательное число, отличное от данных четырёх чисел. Затем она дописывает наименьшее неотрицательное целое число, отличное от четырёх предыдущих чисел и повторяет этот процесс снова и снова. Жора ввёл в машину числа 2, 0, 2, 3. Каким будет 2023-е число в полученном списке?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Последовательность чисел, набранная машиной: 2, 0, 2, 3, 1, 4, 0, 2, 3, 1, 4, 0, 2, 3, 1, 4, 0, 2, 3, … . Заметим, что числа в полученной последовательности, начиная со второго, повторяются пятёрками (0, 2, 3, 1, 4). Удалив первое из 2023 чисел последовательности, мы получим 2022 чисел. Они составляют 1010 полных пятёрок и ещё 2 первых числа в очередной пятёрке, т.е. 0, 2. Поэтому искомым числом является число 2.
|
Задание 23
|
Из прямоугольника на координатной плоскости с вершинами в точках (0, 0), (100, 0), (100, 50) и (0, 50) вырезан круг радиуса 10 с центром в точке (75, 30). Прямая y=kx+b, проходящая через центр круга, делит оставшуюся часть прямоугольника на две равновеликие части. Чему равен угловой коэффициент k этой прямой?
A) 1/5 Б) 1/3 В) 1/2 Г) 2/5 Д) 2/3
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
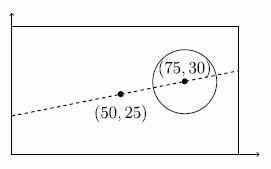
Любая прямая, проходящая через центр
данного прямоугольника (50, 25), делит его на две равновеликие части. Любая прямая, проходящая через центр данного круга (75, 30), также делит этот круг на две равные по площади части. Поскольку окружность целиком лежит внутри прямоугольника, прямая, проходящая через центр прямоугольника и центр данного круга разбивает часть прямоугольника, полученную после вырезания этого круга, на две равновеликие фигуры. Итак, искомым является угловой коэффициент прямой, проходящей через точки (50, 25) и (75, 30). Так как разность между абсциссами этих точек равна 75 – 50 = 25, а разность между ординатами равна 30 – 25 = 5, угловой коэффициент этой прямой равен 5/25 = 1/5
|
Задание 24
|
Когда телефон Мартина полностью заряжен, он разряжается за 32 часа, если используется только для телефонных звонков, через 20 часов, если используется только для интернета, и через 80 часов, если он не используется вообще. Мартин сел в поезд с полузаряженным телефоном. Находясь в поезде, он треть времени на поездку провёл в интернете, треть времени разговаривал по телефону и треть времени телефоном не пользовался. В результате, его телефон разрядился ровно в тот момент, когда поезд прибыл в пункт назначения. Сколько часов заняло путешествие на поезде?
A) 10 Б) 12 В) 15 Г) 16 Д) 18
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Поскольку телефон Мартина заряжен наполовину, время разрядки батареи составляет 16, 10 и 40 часов соответственно при звонках, пользовании интернетом и в неиспользуемом состоянии. Пусть путешествие длилось 3t часов. Тогда за время в дороге телефон разрядился на величину исходного заряда, равную
t/16 + t/10 + t/40 = 3t/16.
А так как, по условию, он разрядился полностью, эта величина равна 1, 3t/16 = 1, откуда время в пути 3t = 16 часов.
|
Задание 25
|
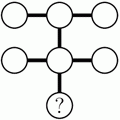
Семь различных однозначных чисел записаны в кружочках данной диаграммы, по одному числу в кружочке. Произведения трёх чисел в каждой из двух строк и среднем столбце, состоящих из трёх чисел, одинаковы. Какое число записано в кружочке со знаком вопроса?
A) 2 Б) 3 В) 4 Г) 6 Д) 8
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Так как произведение чисел в первой строчке равно произведению чисел во второй строчке, то произведение всех шести чисел в этих строчках является полным квадратом. Следовательно, среди чисел в кружочках нет чисел 5 и 7 (эти числа простые, и среди однозначных чисел нет других чисел, которые делятся на 5 или 7). Поэтому в кружках диаграммы записаны числа 1, 2, 3, 4,
6, 8 и 9. Произведение их всех равно
1 · 2 · 3 · 4 · 6 · 8 · 9 = 27 · 34.
Число является полным квадратом, только если в его каноническом разложении показатели степеней простых множителей являются чётными. Поэтому число, которое не может входить в две строчки, – это 2 или 8 = 23. Если в строчках нет числа 8 и оно записано в столбце, то произведение чисел в этом столбце будет кратно 8. С другой стороны, произведение чисел в двух строчках будет равно 24 · 34, и тогда произведение чисел в каждой из этих строчек будет равно 2232 – не делится на 8. Противоречие. Следовательно, в кружочке со знаком вопроса записано число 2.
Так как, по условию, числа уже вписаны, как нужно, то доказывать, что их можно вписать, не требуется. Всё же
приведём пример, удовлетворяющий условию задачи. В первую строчку впишем 1, 9, 8, во вторую – 3, 4, 6. Тогда в столбце будут числа 9, 4, 2. Все произведения равны 72.
|
Задание 26
|
Лёва нарисовал замкнутый путь на поверхности прямоугольного параллелепипеда, а затем развернул его поверхность. Какая из следующих развёрток НЕ может быть развёрткой данного параллелепипеда?

|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
На следующем рисунке серыми линиями показано, какие грани с частями линии станут соприкасаться после сворачивания полученных развёрток в параллелепипед.
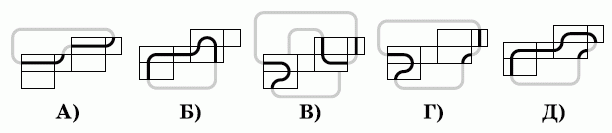
Видим, что во всех вариантах ответа, кроме В), получаются непрерывные замкнутые линии. Поэтому правильным является ответ В.
|
Задание 27
|
Сколько существует трёхзначных натуральных чисел, таких, что при вычитании из них суммы их цифр получается трёхзначное число, все цифры которого одинаковы?
A) 1 Б) 2 В) 3 Г) 20 Д) 30
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть abc – искомое число. Тогда, по условию,
(100a + 10b + c) – (a + b + c) = 99a + 9b – трёхзначное число, у которого все цифры одинаковы.
Кроме того, видим, что это число кратно 9. Согласно признаку делимости на 9, сумма трёх одинаковых цифр такого числа делится на 9. Существует только два таких числа: 333 и 666 (легко видеть, что разность 999 получиться не может).
В первом случае 99a + 9b = 333, или 11a + b = 37, откуда, легко видеть, a = 3, b = 4. Цифра c при вычитании уничтожается и, значит, может быть любой. Поэтому числами abc могут быть 10 чисел: 340, 341, 342, … , 349.
Во втором случае 99a + 9b = 666, или 11a + b = 74, откуда, легко видеть, a = 6, b = 8. Поэтому числами abc могут быть ещё 10 чисел: 680, 681, 682, ... , 689.
Всего получаем 20 чисел, удовлетворяющих условию задачи.
|
Задание 28
|

Сколькими способами можно прочитать слово BANANA в следующей таблице, перемещаясь из одной клетки в другую, соседнюю по стороне? Клетки можно посещать более одного раза.
A) 14 Б) 28 В) 56 Г) 84 Д) другой ответ
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Начинается прочтение слова BANANA с единственной буквы В, расположенной в левой верхней клетке таблицы.
Пусть первой N в нашем слове будет N в центральной клетке. От буквы B к ней существуют 2 пути. Существует
4 способа для выбора второй буквы А. Если второй буквой N также является N в центральной клетке, то последнюю букву A также можно выбрать 4 способами. Итак, существует 2 · 4 · 4 = 32 способа прочитать слово BANANA при условии, что обе буквы N выбраны из центральной клетки.
Пусть вторая буква N отлична от центральной. Существует 3 такие буквы, к каждой можно перейти 2 способами и закончить слово BANANA также 2 способами. Получаем 2 · 3 · 2 · 2 = 24 способа полностью прочитать данное слово.
Пусть теперь первой буквой N является буква в правой верхней клетке (к ней можно перейти от буквы B единственным способом). Если она является и второй в нашем слове, то к ней можно перейти 2 способами и 2 способами закончить слово BANANA. Всего получаем 2 · 2 = 4 способа прочтения. Если второй буквой N является буква в центральной клетке, то к ней можно перейти 2 способами и 4 способами закончить наше слово. Получаем 2 · 4 = 8 способов полного прочтения. Если второй буквой N является буква в правой нижней клетке (к ней можно перейти
от первой буквы N единственным способом), то закончить
слово можно 2 способами. Получаем 2 прочтения. Здесь в общей сложности имеем 4 + 8 + 2 = 14 прочтений.
Ясно, что столько же прочтений, т.е. 14, будет и в том случае, когда первой буквой N будет буква в левой нижней клетке.
Таким образом, общее число всех способов прочтения слова BANANA с соблюдением условия задачи равно
32 + 24 + 14 +14 = 84.
|
Задание 29
|
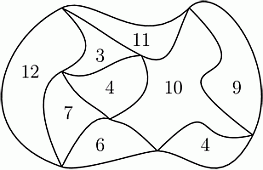
На рисунке показана карта парка. Парк разделён на части. Число внутри каждой части указывает её периметр в км. Каков внешний периметр парка?
A) 22 км
Б) 26 км
В) 28 км
Г) 32 км
Д) другой ответ
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Сумма периметров частей парка A, B, C, D и E даёт длину внешнего периметра парка и штриховой линии на рисунке:
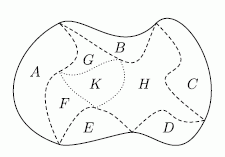
Если вычесть из данной суммы периметры частей F, G и H, то мы вычтем длину штриховой линии, но также вычтем длину пунктирной линии (периметр части K). Поэтому для компенсации к
рассматриваемой разности следует добавить периметр K. Другими словами, обозначив периметры частей парка теми же буквами, что и соответствующие части, получаем: периметр данного парка равен
(A + B + C + D + E) – (F + G + H) + K = (12 + 11 + 9 + 4 + 6) – (7 + 3 + 10) + 4 = 42 – 20 + 4 = 26 км.
|
Задание 30
|
Полина хочет вписать целые числа от 1 до 9 в девять клеток строки так, чтобы суммы чисел в любых трёх подряд идущих клетках были кратны 3. Сколькими способами она может это сделать?

A) 64
Б) 63
В) 29
Г) 6∙5∙4∙3∙2∙1
Д) 9∙8∙7∙6∙5∙4∙3∙2∙1
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Рассмотрим 4 подряд идущих числа. Первые 3 из них и последние 3 из них должны иметь суммы, кратные 3. При этом два слагаемых у этих сумм общие. Поэтому первое и четвёртое числа в данной четвёрке должны
иметь одинаковые остатки при делении на 3. Следовательно, остатки чисел в строке должны повторяться с периодом 3. Другими словами, последовательность остатков чисел данной строки имеет вид ABCABCABC, где A, B, C принимают различные значения из множества {0, 1, 2}. Существует 3 способа выбрать значение для остатка А, после этого – 2 способа выбрать остаток для В, после чего – только 1 способ выбрать третий остаток С. Всего имеем
3! = 3 · 2 · 1 = 6 способов распределения остатков 0, 1 и 2 между А, В и С.
После этого есть 6 = 3! способов расстановки чисел с остатком 0 (т.е. чисел 3, 6 и 9) на 3 соответствующие этому остатку позиции. Как только эти числа расставлены, есть 6 способов распределить числа с остатком 1 (числа 1, 4 и 7) на соответствующие места. Наконец, есть 6 способов расставить числа с остатком 2 (числа 2, 5 и 8) на оставшиеся 3 места. Всего получаем
6 · 6 · 6 · 6 = 64 расстановок, удовлетворяющих условию задачи.
|