Задание 1
|
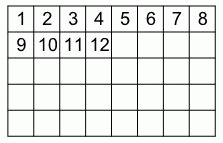
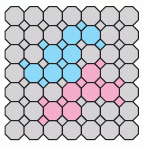
Ольга заполняет таблицу на рисунке числами от 1 до 40 по порядку, как показано на рисунке. Какой из следующих фрагментов можно вырезать из этой целиком заполненной таблицы?
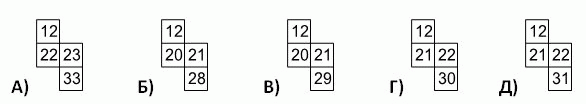
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 30 + 3 = 33
|
В каждой строчке 8 клеток. Поэтому, согласно способу заполнения таблицы, каждое число, начиная с чисел второй строчки, будет на 8 больше вышестоящего. В вариантах ответа только в варианте В для обоих нижестоящих чисел (20 и 29) выполняются эти условия. Поэтому правильный ответ – ответ В.
Задание 2
|

Числа из спичек можно строить так, как показано на рисунке. При этом число 15 можно построить с помощью 7 спичек, и столько же спичек нужно, чтобы построить число 8. Какое наибольшее число можно построить с помощью 7 спичек?
A) 31 Б) 51 В) 74 Г) 711 Д) 800
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Число Д) 800 сложить из 7 спичек невозможно. Для этого понадобилось бы 7 + 6 + 6 = 19 спичек. Числа в первых четырёх вариантах ответа сложить из 7 спичек можно. Наибольшим из них является число Г) 711.
Задание 3
|
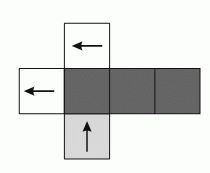
Роза свернула кубик из развёртки, показанной на рисунке. Какой из следующих кубиков у неё мог получиться?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Для удобства заменим рисунки на цветные
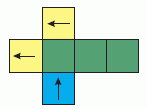

Из развёртки видно, что голубая грань кубика противоположна одной из жёлтых граней и является соседней с другой жёлтой гранью. Это исключает ответ А), в котором голубая грань соседствует с обеими жёлтыми. Далее, видно, что после сворачивания развёртки обратно в кубик стрелки на голубой и соседней с ней жёлтой гранях будут расположены параллельно друг другу и направлены в противоположные стороны (одна вверх, другая вниз; одна влево, другая вправо и т.п.) – это исключает ответы В) и Д). А вот стрелки на соседних жёлтых гранях не будут параллельны, т.к. одна из них параллельна общему ребру этих граней, а другая направлена на него – это исключает ответ Г). Остался единственный (а значит, правильный) ответ Б), который не противоречит развёртке.
Задание 4
|
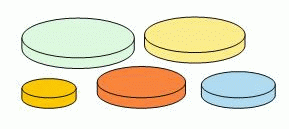
У Ани есть пять круглых дисков разного размера. Она хочет построить башню из четырёх дисков так, чтобы каждый диск, расположенный выше, был меньше диска, расположенного ниже. Сколько разных башен может построить Аня?
A) 4 Б) 5 В) 9 Г) 12 Д) 20
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Чтобы выбрать четыре диска из данных пяти дисков, нужно один диск из полного набора удалить. Удалить один диск из пяти можно пятью способами. Получим 5 различных наборов дисков. Все четыре оставшихся диска в этих наборах имеют разные размеры. Поэтому башня из каждого такого набора с соблюдением условия задачи строится однозначно. Следовательно, Аня может построить 5 разных башен.
Задание 5
|

Коля поднимается снизу вверх по чёрным ступенькам цилиндрической башни. Все ступеньки имеют одинаковый размер. На рисунке видны девять ступенек, по которым он прошёл. Сколько ступенек на его пути не видно на рисунке?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
На рисунке видно 9 чёрных ступенек (некоторые – частично). Всего у башни 21 слой. С каждой следующей на пути ступенькой Коля поднимается на 1 слой. Поэтому, чтобы подняться наверх, Коле нужно пройти 21 ступеньку. Так как на рисунке видно 9 чёрных ступенек, то не видно
21 – 9 = 12 чёрных ступенек.
Задание 6
|
Какую из следующих фигур нельзя разрезать по прямой линии на 2 треугольника?

|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 33.75 - 0.75 = 33
|
Треугольник разрезается на два треугольника по линии, проходящей через вершину и любую внутреннюю точку
противоположной стороны. Фигуры Б), В) и Д) – четырёхугольники. Их можно разрезать на два треугольника по диагонали. Шестиугольник на два треугольника разрезать нельзя. Наименьшее число вершин у двух частей, полученных после разрезания шестиугольника, будет, если разрез сделан по диагонали, и оно равно 6 + 2 = 8. А у двух треугольников число вершин равно 3 + 3 = 6. Поэтому шестиугольник нельзя разрезать на два треугольника. Таким образом, правильным является ответ Г).
Задание 7
|
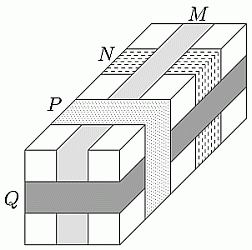
На рисунке изображена посылка, оклеенная четырьмя лентами M, N, P и Q. В каком порядке наклеивались эти ленты (от первой до последней)?
A) M, N, Q, P
Б) N, M, P, Q
В) N, Q, M, P
Г) N, M, Q, P
Д) Q, N, M, P
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Лента P наклеена поверх всех других лент. Поэтому она наклеена последней. Далее, видно, что лента Q наклеена поверх M и N. Поэтому лента Q наклеена предпоследней. Наконец, лента M наклеена поверх ленты N. Поэтому лента N наклеена первой, а лента M – второй. В результате видим, что ленты были наклеены в порядке N, M, Q, P.
Задание 8
|
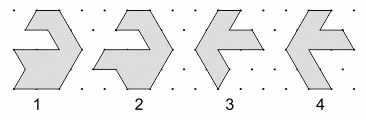
У Алисы есть 4 плитки пазла. Из каких двух можно сложить 6-угольник?
A) 1 и 2
Б) 1 и 3
В) 2 и 3
Г) 2 и 4
Д) 1 и 4
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Дополним каждую из фигур 1 – 4 до шестиугольника соответствующих размеров так, как показано на рисунке.
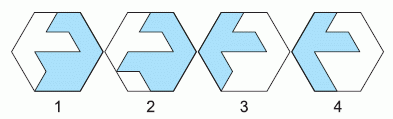
Видим, что шестиугольник образуют фигуры 1 и 3.
Задание 9
|
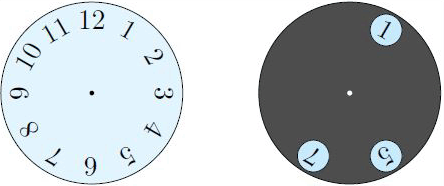
Чёрный круг с тремя отверстиями наложили сверху на циферблат. Какие следующие три числа можно одновременно увидеть в отверстиях, если вращать чёрный круг вокруг его центра?
A) 2, 4 и 9
Б) 1, 5 и 10
В) 4, 6 и 12
Г) 3, 6 и 9
Д) 5, 7 и 12
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 31.5 - 0.75 = 30.75
|
На рисунке в условии задачи видно следующее. Если смотреть по ходу часовой стрелки, то разность между числами в первом и втором отверстиях равна 4, разность между числами во втором и третьем отверстиях равна 2. При этом первое и третье отверстия диаметрально противоположны, и разница между числами в них равна 6. В вариантах ответа А) 2, 4 и 9, Б) 1, 5 и 10, Д) 5, 7 и 12 нет чисел, разность которых равна 6. В ответе Г) нет чисел, разность которых равна 2. Поэтому названные ответы не являются верными. А ответ В) 4, 6 и 12 всем условиям удовлетворяет. Он получится, если повернуть чёрный круг на 1 единицу против хода часовой стрелки.
Задание 10
|
Гена наклеил три листа бумаги
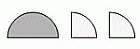
на чёрный круг соответствующего размера.

Какой из следующих результатов он НЕ мог получить?

|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 30.75 - 0.75 = 30
|
Серый лист – это полукруг. Поэтому после наклейки всех листов серая часть полученного результата – это либо весь
данный полукруг, либо какая-то его часть, не покрытая белыми четвертями круга. С учётом сказанного результат В) получиться не мог. Несложно убедиться, что остальные результаты получить можно. Таким образом, правильный ответ – ответ В).
Задание 11
|
Франческа записала три последовательных двузначных числа в порядке их возрастания, затем она цифры заменила символами и получила:
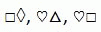
Как с помощью таких символов запишется следующее по величине число?
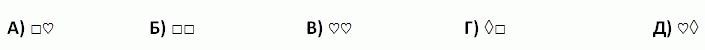
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 30 - 1 = 29
|
Задание 12
|
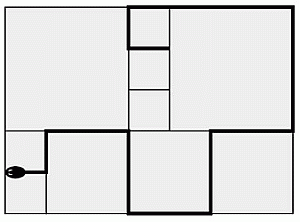
У Поттеров есть внутренний дворик, выложенный квадратной плиткой трёх разных размеров. Самые маленькие плитки имеют периметр 80 см. Змея отдыхает во внутреннем дворике, как показано на рисунке. Какова длина змеи?
A) 380 см Б) 400 см В) 420 см Г) 440 см Д) 160 см
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 29 - 1 = 28
|
Из условия следует, что сторона маленькой плитки равна
80 : 4 = 20 см.
Тогда сторона средней плитки равна
20 · 2 = 4 см,
а сторона самой большой плитки равна
20 · 3 = 60 см (см. рис. в условии задачи).
Змея по длине составляет 5 сторон маленьких плиток, 5 сторон средних плиток и 2 стороны больших плиток. Поэтому длина змеи равна
5 · 20 + 5 · 40 + 2 · 60 = 420 см.
Задание 13
|
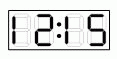
Когда я смотрю в зеркало на часы, расположенные на столе позади меня, я вижу то, что изображено на рисунке. Что я увижу в зеркале через 30 минут?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 28 + 4 = 32
|
В зеркале цифры будут видны в обратном порядке, причём вместо цифры 2 будет видна симметричная ей цифра 5, а вместо цифры 5 – цифра 2. Поэтому, если в зеркале часы показывают 12:15, то реальное время 21:51. Через 30 минут время на часах будет 22:21. Поэтому в зеркале часы будут показывать 15:55.
Задание 14
|
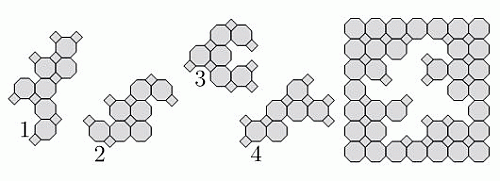
Какие две из следующих плиток нужны, чтобы закончить пазл на рисунке?
A) 1 и 2
Б) 1 и 4
В) 2 и 3
Г) 2 и 4
Д) 3 и 4
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 32 - 1 = 31
|
На рисунке показано, как выглядит завершённый пазл с выделенными недостающими элементами. Видим, что для окончания сборки нужны плитки 2 и 4.
Задание 15
|
Маша, Петя, Рита и Толя играли с мячом в классе и кто-то из них разбил окно. На вопрос директора, кто это сделал, были получены ответы: Маша: «Это Петя». Петя: «Это Рита». Рита: «Это не я». Толя: «Это не я». Только кто-то один из них сказал правду. Кто разбил окно?
A) Маша
Б) Толя
В) Петя
Г) Рита
Д) нельзя определить однозначно
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 31 - 1 = 30
|
Если Рита говорит правду, то Петя врёт, и наоборот, если Рита врёт, то Петя говорит правду. Поскольку, по условию, только один школьник говорит правду, то это либо Петя, либо Рита. Следовательно, Маша и Толя врут. А так как Толя говорит,
что не он разбил окно и при этом он врёт, то именно он – Толя – разбил окно.
Задание 16
|

На рисунке показаны пять прямоугольников. Лукас хочет раскрасить прямоугольники в красный, синий и жёлтый цвета так, чтобы любые два соседних прямоугольника были окрашены в разные цвета. Сколькими различными способами это можно сделать?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 30 - 1 = 29
|
Заметим, что средний верхний прямоугольник является соседним со всеми другими 4 прямоугольниками. Поэтому, если данный прямоугольник окрашен в какой-то цвет (это можно сделать 3 способами, и пусть выбран
цвет №1), то остальные прямоугольники могут быть окрашены только с помощью двух цветов №2 и №3. При этом существует
только два способа окраски этих четырёх прямоугольников (см. рис.)
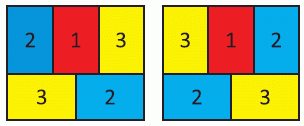
Всего получаем 3 · 2 = 6 различных раскрасок.
Задание 17
|
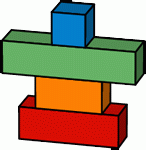
Игорь сложил четыре коробки, как показано на рисунке:
За один ход он может взять несколько или все блоки с вершины стопки и перевернуть их вверх ногами, например:
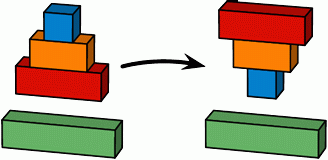
Игорь хочет, чтобы блоки были сложены в следующем порядке:
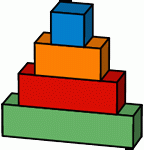
Какое наименьшее количество ходов ему для этого нужно сделать?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 29 + 4 = 33
|
Блоки в порядке возрастания размеров расположены как 1423. Их нужно расположить в порядке 1234. За один раз
это сделать нельзя, так как блок 1 окажется не на своём месте. За два хода также нельзя расположить блоки так, как требуется. Действительно, блок 1 уже находится на нужной позиции. После первого хода он переместится на неподходящую позицию. Для того чтобы вторым ходом его вернуть обратно, необходимо сделать обратный ход. В результате получим начальное расположение блоков. Итак, необходимо не менее трёх ходов. С другой стороны, за три хода упорядочить блоки, как требуется в условии, можно:
1423 → 4123 → 3214 → 1234 (см. также рис.)

Задание 18
|
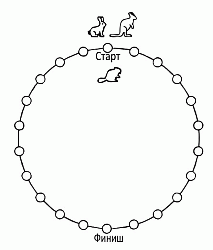
Кролик, бобёр и кенгуру соревнуются. Бобёр перемещается на одну позицию за один ход, кролик ─ на две, а кенгуру ─ на три. Все начинают движение одновременно в одном направлении с точки Старт. Победителем становится тот, кто первым в точности окажется в точке Финиш за наименьшее количество полных ходов. Кто выиграет в конкурсе?
A) бобёр
Б) кролик
В) кенгуру
Г) кенгуру и кролик
Д) кенгуру и бобёр
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33 + 4 = 37
|
Всего на круговой дистанции имеется 22 позиции. «Финиш» находится на 11-й после «старта» позиции. Поэтому
Бобёр достигнет «финиша» через 11 ходов. Кролик на первом круге
пропускает «финиш» и возвращается в позицию «старт». Следовательно, и далее он будет пропускать позицию «финиш» и никогда на ней не окажется. Кенгуру на первом круге пропускает позицию «финиш». Но его скорость в 3 раза больше скорости Бобра. Поэтому за то время, как Бобёр переместится на половину круга и окажется в позиции «финиш», Кенгуру переместится на полтора круга и тоже окажется на позиции «финиш». Видим, что правильным является ответ Д Кенгуру и Бобёр.
Задание 19
|
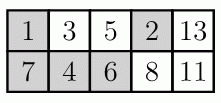
Лена хочет, чтобы сумма чисел в белых клетках таблицы была равна сумме чисел в серых клетках. Какие два числа из чисел этой таблицы ей нужно для этого поменять местами?
A) 1 и 11
Б) 2 и 8
В) 3 и 7
Г) 4 и 13
Д) 7 и 13
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 37 - 1 = 36
|
Сумма чисел в серых клетках таблицы равна
1 + 2 + 7 + 4 + 6 = 20,
а сумма чисел в белых клетка равна
3 + 5 + 13 + 8 + 11 = 40.
Разность между ними равна
40 – 20 = 20.
Чтобы уравнять эти суммы, первую нужно увеличить на
20 : 2 = 10,
а вторую уменьшиться на 10. Поэтому поменять местами нужно числа в серой и белой клетках, такие, что число в серой клетке на 10 меньше числа в белой клетке. Легко видеть, что такими являются только числа 1 и 11.
Задание 20
|
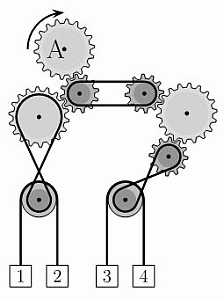
Шестерня A вращается по часовой стрелке, как показано на рисунке. Какие два ящика будут двигаться вверх?
A) 1 и 4
Б) 2 и 3
В) 1 и 3
Г) 2 и 4
Д) невозможно определить
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 36 - 1 = 35
|
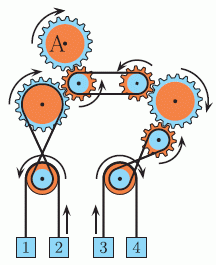
На рисунке показаны направления движения всех шестерён. На этом рисунке видно, что будут подниматься ящики вверх 2 и 3.
Задание 21
|
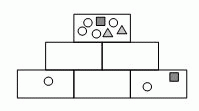
Тина хочет нарисовать фигуры на шести коробках, образующих пирамиду. На каждой верхней коробке должны быть в точности все фигуры, которые нарисованы на двух соседних нижних коробках прямо под нею, и ничего более. Тина уже нарисовала некоторые фигуры на трёх коробках. Какие фигуры она должна нарисовать на средней коробке в нижнем ряду?

|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 35 - 1.25 = 33.75
|
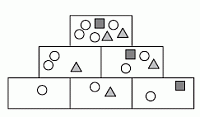
Согласно условию, на двух коробках в среднем ряду в совокупности должно быть 4 кружочка, два треугольника и 1 квадратик. Два кружочка и квадратик «переходят» во второй ряд из крайних коробок нижнего ряда. Затем они «переходят» на верхнюю коробку пирамиды. Остальные 4 – 2 = 2 кружочка и 2 треугольника должны «добавиться» к ним из коробок нижнего ряда. Средняя коробка нижнего ряда «передаёт» в коробки вышестоящего ряда двойной вклад. Поэтому в ней должна быть половина от того, что нужно «добавить» во второй ряд, т.е. 1 кружочек и 1 треугольник. Таким образом, правильным является ответ Г. Ниже приведён соответствующий рисунок.
Задание 22
|
У Лизы есть два аппарата. Когда Лиза кладёт квадратный лист бумаги в аппарат R, он поворачивает лист на 90° по часовой стрелке, как показано на рисунке. Когда Лиза кладет лист в аппарат S, он штампует на нём символ  .
.
В каком порядке следует использовать аппараты для получения показанного ниже результата?
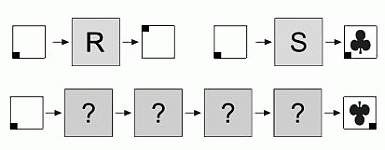
A) SRRR Б) RSRR В) SRSR Г) RRRS Д) SRRS
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
На рисунке в условии видно, что лист бумаги должен быть повёрнут 3 раза, 2 из них – после того, как напечатан штамп. Следовательно, правильным является ответ RSRR.
Задание 23
|
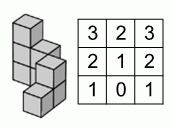
Марта выбрала одну из пяти фигур в вариантах ответа и склеила её с фигурой на рисунке выше. В таблице показано количество кубиков в каждом столбике полученной при склеивании фигуры, если посмотреть на неё сверху. Какую из следующих пяти фигур выбрала Марта?

|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 32.5 - 1.25 = 31.25
|
Фигура на рисунке в условии задачи состоит из
3 + 2 + 2 + 1 = 8 кубиков.
Конструкция, которую нужно получить,
должна состоять из
3 + 2 + 3 + 2 + 1 + 2 + 1 + 0 + 1 = 15 кубиков (считаем по таблице в условии задачи).
Поэтому Марта выбрала фигуру, состоящую из
15 – 8 = 7 кубиков.
Непосредственные подсчёты показывают, что только фигура Г) состоит из 7 кубиков. И её действительно можно склеить с фигурой в условии так, что получится нужная конструкция. Поэтому правильным является ответ Г.
По-другому найти этот ответ можно так. Рассмотрим таблицу конструкции, которую склеила Марта (см. рис.).

В ней красным цветом окрашены клетки столбцов, которые по количеству кубиков в точности совпадают со столбцами фигуры из условия задачи. Поэтому белые клетки в этой таблице в точности определяют искомую фигуру. Числа в белых клетках
указывают высоту столбцов, а расположение клеток – расположение соответствующих столбцов. Просматривая варианты ответа, видим, что белые клетки таблицы и числа в них определяют фигуру Г).
Задание 24
|
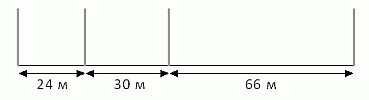
Вдоль 120-метровой дорожки размещены четыре столба, как показано на рисунке. Какое наименьшее количество столбов нужно добавить, чтобы они разделяли дорожку на участки одинаковой длины?
A) 12 Б) 15 В) 17 Г) 20 Д) 37
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 31.25 + 5 = 36.25
|
Чтобы расстояния между соседними столбами было одинаковым, это расстояние (в метрах) должно быть делителем
чисел 24, 30 и 66.
НОД (24, 30, 66) = 6.
Поэтому наименьшее число промежутков между столбами должно быть равно
120 : 6 = 20.
Тогда число столбов будет равно
20 + 1 = 21.
Первоначально имеется 4 столба. Поэтому нужно добавить
21 – 4 = 17 столбов.
Задание 25
|
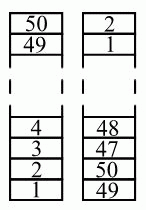
На столе стоит башня, состоящая из блоков, пронумерованных по порядку снизу вверх числами от 1 до 50. Эмма строит новую башню следующим образом. Она берет два блока с вершины исходной башни и кладёт их на стол в качестве основания новой башни. Затем она берёт следующие два верхних блока из оставшейся части исходной башни и кладёт их на вершину новой башни, как показано на схеме, и т. д. Какие из следующих пар чисел окажутся на соседних блоках в новой башне?
A) 29 и 28
Б) 34 и 35
В) 29 и 26
Г) 31 и 33
Д) 27 и 30
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 36.25 - 1.25 = 35
|
Заметим, что в новой башне под каждым блоком с чётным номером n находится блок с нечётным номером n – 1. А над каждым блоком с чётным номером n находится блок с нечётным номером n – 3. Из предложенных вариантов ответа эти условия выполняются только в ответе Д) 27 и 30.
Задание 26
|
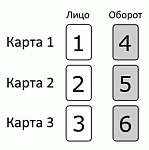
У Мартина есть три карточки с цифрами, написанными с обеих сторон. На первой карте записаны цифры 1 и 4, на второй – 2 и 5, на третьей – 3 и 6. Мартин случайным образом кладёт три карты на стол и складывает три числа, которые он видит сверху. Сколько различных сумм он может получить?
A) 3 Б) 4 В) 5 Г) 6 Д) 10
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 35 - 1.25 = 33.75
|
Наименьшая из сумм, которые можно получить, равна
1 + 2 + 3 = 6.
Далее заметим, что у каждой карточки число на обороте на 3 больше числа на лицевой стороне. Поэтому, перевернув любую из карточек с числами 1, 2 или 3, мы увеличим сумму на 3 и получим значение 9. Перевернув ещё одну карточку (обратной стороной вверх), мы увеличим сумму ещё на 3 и получим 12. Наконец, перевернув третью карточку, получим сумму 15. Таким образом, Мартин может получить только 4 различные суммы: 6, 9, 12 и 15.
Задание 27
|
В секонд-хенде 2 шляпы продаются по той же цене, что и 5 юбок, 3 юбки – по той же цене, что и 8 футболок, и 2 футболки – по той же цене, что и 3 кепки. Какая из следующих коллекций является наиболее дорогой?
A) 1 шляпа и 5 юбок
Б) 1 шляпа, 3 юбки и 1 кепка
В) 8 юбок и 6 футболок
Г) 37 кепок
Д) 3 юбки и 3 кепки
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
Вычислим в «кепках» стоимости указанных в ответах наборов. Согласно условию,
2 футболки = 3 кепки, откуда
1 футболка = 1,5 кепки;
3 юбки = 8 футболок = 12 кепок, откуда
1 юбка = 4 кепки;
2 шляпы = 5 юбок = 20 кепок, откуда
1 шляпа = 10 кепок.
Тогда
А) 1 шляпа + 5 юбок = 10 + 5 · 4 = 30 кепок;
Б) 1 шляпа + 3 юбки + 1 кепка = 10 + 3 · 4 + 1 = 23 кепки;
В) 8 юбок + 6 футболок = 8 · 4 + 6 · 1,5 = 41 кепка;
Г) 37 кепок;
Д) 3 юбки + 3 кепки = 3 · 4 + 3 = 15 кепок.
Видим, что наиболее дорогим является комплект В) 8 юбок и 6 футболок.
Задание 28
|
Соня и Роберт играют в следующую игру. Они по очереди берут 1, 2, 3, 4 или 5 плиток из стопки. Проигрывает тот, кто возьмёт последнюю плитку. В какой-то момент игры в стопке осталось 10 плиток, и настала очередь Сони сделать ход. Сколько плиток должна Соня оставить Роберту, чтобы быть уверенной, что она выиграет?
A) 9 Б) 8 В) 7 Г) 6 Д) 5
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32.5 + 5 = 37.5
|
Если игроку останется одна плитка, то этот игрок проиграет. Если игроку осталось 2, 3, 4, 5 или 6 плиток, то этот игрок после своего хода может оставить 1 плитку противнику и, тем самым, выиграет. Если игроку осталось 7 плиток, то после своего хода он может оставить 2, 3, 4, 5 или 6 плиток и, значит, его противник выиграет. Итак, если Соня возьмёт 3 плитки и оставит 7 плиток, то она выиграет. Если же она оставит 8 или 9 плиток, то после этого Роберт сможет оставить 7 и, тем самым, он выиграет, а Соня проиграет. Видим, что правильным является ответ 7.
Задание 29
|
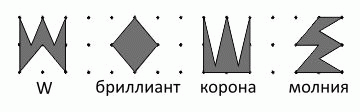
Какая из следующих фигур имеет наибольшую площадь?
A) W
Б) бриллиант
В) корона
Г) молния
Д) у всех площади равны
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 37.5 + 5 = 42.5
|
Все данные фигуры можно считать вписанными в квадрат 2 × 2. Определим, какую по площади часть этого квадрата они составляют. Это легко сделать, если предварительно данные фигуры и квадраты 2 × 2 разбить на части, как показано на следующем рисунке.
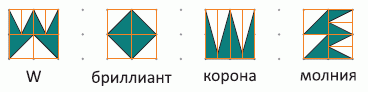
Видим, что фигуры W, бриллиант и молния по площади составляют ровно половину квадрата 2 × 2, а площадь фигуры корона больше половины квадрата, так как точки ломанной, образующей фигуру, лежат выше нижнего основания квадрата.
Задание 30
|
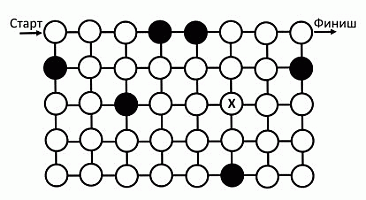
Исследователь хочет найти путь в лабиринте от точки Старта до точки Финиша. Он может двигаться только по горизонтали или по вертикали и проходить только через белые кружочки, через каждый – ровно один раз. Каким будет шаг после кружочка с буквой X?
A) ↑
Б) ↓
В) →
Г) ←
Д) такого пути не существует
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 42.5 - 1.25 = 41.25
|
Будем строить искомый путь частями. Заметим, что если какие-то белые кружочки соединены отрезками с 1 или 2 другими белыми кружочками, то соединяющие их отрезки обязаны быть частями искомого пути. Окрасим эти кружочки в зелёный цвет и проведём соответствующие отрезки (тоже зелёного цвета; см. первый рис.).
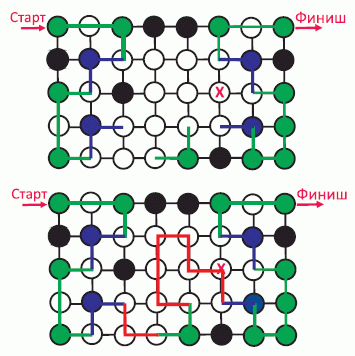
После этого рассмотрим кружочки синего цвета. Их четыре, и их можно соединить не более чем с двумя соседними кружочками, которые ещё не являются промежуточными на построенных участках пути. Добавим соответствующие отрезки к уже построенным (на рисунке они синего цвета). Теперь рассмотрим кружочек, отмеченный символом X. Отрезками пути, которые через него проходят, могут быть только отрезок слева от данного
кружочка и отрезок внизу. Легко видеть, что отрезок слева может быть только входящим, а отрезок внизу – выходящим из данного кружочка. Таким образом, правильным является ответ Б) ↓. После этого несложно добавить недостающие звенья, чтобы получить весь путь (см. нижний рисунок). Видим, что путь, удовлетворяющий условию задачи, строится однозначно.




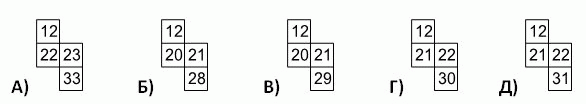
















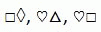
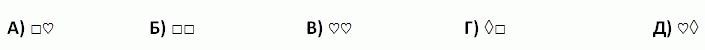
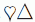 , следующего после первого числа
, следующего после первого числа 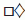 , изменились обе цифры. Следовательно,
, изменились обе цифры. Следовательно, 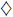 = 9,
= 9, 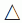 = 0. А тогда у
следующего после
= 0. А тогда у
следующего после  цифра
цифра 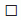 = 1. Итак, первое число – это число 19. Тогда второе число равно 20, в частности,
= 1. Итак, первое число – это число 19. Тогда второе число равно 20, в частности,  = 2. Поэтому число
= 2. Поэтому число 


















 .
.










