Задание 1
|
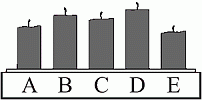
Аня одновременно зажгла 5 одинаковых свечей, которые сгорают с одинаковой скоростью. Свечи перестали гореть в разное время и теперь выглядят так, как показано на рисунке. Какая свеча погасла первой?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 24 + 3 = 27
|
По условию, все свечи одинаковые и горели с одинаковой скоростью. Поэтому первой погасла та свеча, у которой
осталась наибольшая часть. Такой является свеча D.
Задание 2
|
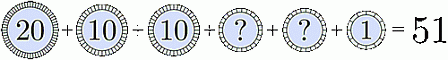
На рисунке две монеты, отмеченные знаком вопроса, имеют одинаковую стоимость. Какова их стоимость
A) 1 Б) 2 В) 5 Г) 10 Д) 20
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 27 + 3 = 30
|
Согласно условию, стоимость двух монет, отмеченных знаком «?», равна
51 – 20 – 10 – 10 – 1 = 10.
Поэтому стоимость одной такой монеты равна
10 : 2 = 5.
Задание 3
|
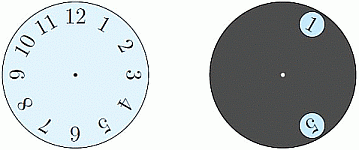
Чёрный круг с двумя отверстиями наложили сверху на циферблат, как показано на рисунке. Какие из следующих чисел можно увидеть одновременно, если повернуть чёрный круг вокруг его центра
A) 4 и 9
Б) 5 и 9
В) 5 и 10
Г) 6 и 9
Д) 7 и 12
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 30 + 3 = 33
|
На рисунке в условии задачи видно, что следующее по ходу часовой стрелки число (если идти по кратчайшей дуге) на 4 больше предыдущего. Ясно, что это свойство будет сохраняться и при поворотах. (Если при повороте вместо числа 5 появится меньшее число, то, чтобы сохранилось данное свойство, это число следует увеличить на 12.) Рассматривая варианты ответов, находим, что данному
условию удовлетворяют только числа 5 и 9.
Задание 4
|
У Аллы есть фигурки. Из каких двух из них можно сложить квадрат?
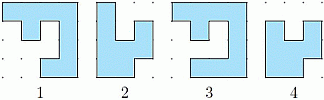
A) 1 и 2
Б) 1 и 3
В) 1 и 4
Г) 2 и 3
Д) 2 и 4
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 33 + 3 = 36
|
Из условия задачи следует, что данные
фигуры можно разбить на одинаковые квадратные клетки (см. рис.).
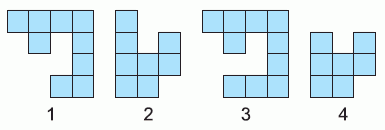
При этом фигура 1 состоит из 9 клеток, фигура 2 – из 8 клеток, фигура 3 – из 10 клеток, фигура 4 – из 7 клеток. Если из этих двух фигур можно сложить квадрат, то число клеток в этом квадрате должно быть квадратом натурального числа. Учитывая размеры фигур, клеток в таком квадрате может быть только 16. Поэтому фигуры 2 и 3 не подходят. А подходят фигура 4 из 7 клеток и фигура 1 из 9 клеток, так как 7 + 9 = 16. Поэтому возьмём фигуру 4 и дорисуем её до квадрата 4 × 4 (см. рис.).
Видим, что второй фигурой в этом квадрате является фигура 1. Таким образом, правильным является ответ В.
Задание 5
|
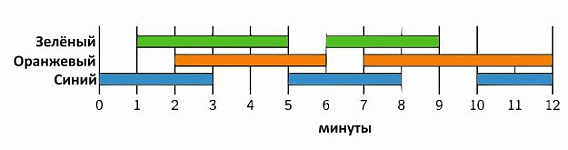
Светотехник в театре включает и выключает свет согласно плану на рисунке. Сколько минут в общей сложности ровно 2 лампы горят одновременно?
A) 62 Б) 86 В) 8 Г) 9 Д) 10
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 36 - 0.75 = 35.25
|
На диаграмме в условии задачи показаны 12 минут, в течение которых горят какие-то из трёх ламп. Ровно 2 лампы горят
с 1-й до 2-й минуты (2 – 1 = 1 минута),
с 3-й по 7-ю минуту (7 – 3 = 4 минуты),
с 8-й по 9-ю минуту (9 – 8 = 1 минута) и
с 10-й по 12-ю минуты (12 – 10 =2 минуты).
Таким образом, в общей сложности за указанное время ровно две лампы горят
1 + 4 + 1 + 2 = 8 минут.
Задание 6
|
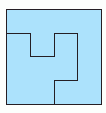
Костя согнул прозрачную бумагу по пунктирной линии.
Что он может видеть в результате?

|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Дорисуем в нижней половине листа те отрезки, которые добавит верхняя половина листа после сгибания (см. рис.).
Эти отрезки отобразятся симметрично относительно линии сгибания. Видим, что правильным является ответ Д.
Задание 7
|
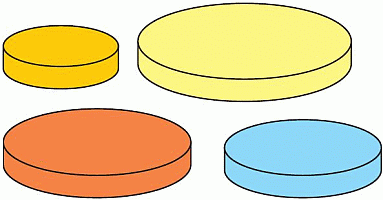
У Ани есть 4 диска разного размера. Она хочет построить башню из трёх дисков так, чтобы каждый верхний диск был меньше нижнего. Сколько разных башен может построить Анна?
A) 1 Б) 2 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
Удалить один из четырёх дисков можно четырьмя способами. Получим 4 различных набора дисков. Все три оставшихся диска в этих наборах имеют разные размеры. Поэтому башня из каждого такого набора строится однозначно. Следовательно, Аня может построить 4 разные башни.
Задание 8
|
Дима наклеил 2 листа бумаги  поверх чёрного круга соответствующего размера
поверх чёрного круга соответствующего размера  .
.
Что у него НЕ могло получиться?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33.75 + 3 = 36.75
|
Дима не может получить результат Д. Рассмотрим серые части. В ответе Д две серые части в совокупности по площади составляют половину круга. Но эти части (в ответе Д) не являются соседними и не образуют половину круга. А в условии задачи серая фигура – это в точности половина круга. Нетрудно убедиться, что склейки в других вариантах ответа получить можно.
Задание 9
|
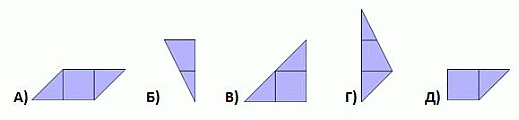
Петя сложил «угол» из фигур, указанных ниже.
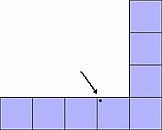
Какая из них покрыла отмеченную точку?
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 36.75 - 1 = 35.75
|
Понятно, что фигура В – угловая часть построенного Петей «угла» (см. рис.1).
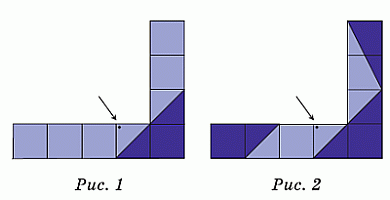
Далее, нужно покрыть 3 с половиной клетки на горизонтальной стороне «угла» и 2 с половиной клетки на вертикальной стороне. 3 с половиной клетки составляют либо фигуры А и Г, либо А и Д. Таким образом, фигура А должна быть расположена на горизонтальной стороне «угла». И тогда она может быть расположена только так, как на рисунке 2. На нём показаны расположения и всех других фигур. Видим, что правильным является ответ А.
Задание 10
|
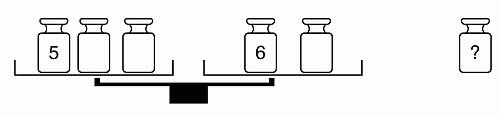
Имеется шесть гирь весом 1, 2, 3, 4, 5 и 6 кг. Рая кладёт пять из них на весы так, как показано на рисунке, и откладывает одну гирю в сторону. Весы оказались сбалансированы. Гирю какого веса отложила Рая?
A) 1 Б) 2 В) 3 Г) 4 Д) невозможно определить
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.75 + 4 = 39.75
|
Сумма весов всех данных гирь
1 + 2 + 3 + 4 + 5 + 6 = 21 кг – нечётная.
Если чаши весов сбалансированы, то веса гирь на этих чашах равны. Поэтому суммарный вес всех гирь на весах выражается чётным числом. Чтобы из рассматриваемой суммы, равной 21, получить чётную сумму, нужно убрать нечётное слагаемое. Поэтому Рая отложила либо гирю в 1 кг, либо гирю в 3 кг (гиря в 5 кг использована). В первом случае получаем сумму
2 + 3 + 4 + 5 + 6 = 20 кг,
и тогда веса гирь на чашах должны быть равны
20 : 2 = 10 кг.
Разложить соответствующие гири по чашам надлежащим образом можно:
5 + 3 + 2 кг на левой чаше и
4 + 6 кг – на правой.
Если удалить гирю весом 3 кг, то на весах будет
1 + 2 + 4 + 5 + 6 = 18 кг.
Тогда на каждой чаше будет по 9 кг. Но 9 кг на левой чаше можно получить только как 5 + 4, а на правой – как 6 + 1 + 2. В частности, на левой чаше будут
2 гири, а на правой – 3 гири. Однако, по условию, всё наоборот. Поэтому правильным является ответ А.
Задание 11
|
У Оли есть линейка длиной 60 см. Некоторые надписи на линейке стёрлись. Но Оля может измерить любую из длин 10, 20, 30, 40, 50 и 60 см. Какой из следующих линеек она может это сделать?

|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 39.75 - 1 = 38.75
|
С помощью линейки А нельзя измерить расстояние 40 см.
С помощью линейки Б нельзя измерить расстояние 10 см (а также 30 см и 50 см).
С помощью линейки В нельзя измерить расстояние 40 см.
С помощью линейки Г нельзя измерить расстояние 30 см.
Линейка Д позволяет измерить все названные расстояния.
Задание 12
|
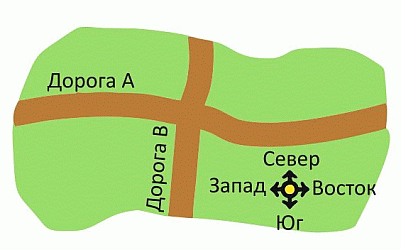
К северу от дороги А находятся 7 домов, к востоку от дороги B - 8 домов и 5 домов - к югу от дороги A. Сколько домов на западе от дороги В?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 38.75 - 1 = 37.75
|
Дома к северу от дороги А и к югу от дороги А – это все дома на карте. Поэтому их количество равно 7 + 5 = 12. Число домов на востоке от дороги В равно 8. Поэтому число домов на западе от этой дороги В равно 12 – 8 = 4.
Задание 13
|
В очереди на паром стоят 8 машин. В каждой машине 2 или 3 человека. Всего паром ожидают 19 человек. Сколько автомобилей вмещают ровно по 2 человека?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.75 + 4 = 41.75
|
Представим себе мысленно, что из каждой машины с тремя людьми один человек выйдет. Тогда все 8 машин будут с двумя пассажирами, а значит, в машинах будет
8 × 2 = 16 человек.
Следовательно вышло из машин
19 – 16 = 3 человека.
Это означает, что машин с тремя людьми на пароме 3, а тогда машин с двумя
8 – 3 = 5.
Задание 14
|
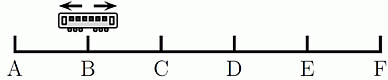
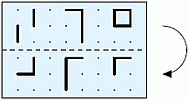
На линии метро 6 станций, А, В, С, D, Е и F. Поезд останавливается на каждой станции. Когда поезд достигает одной из двух конечных станций, он меняет свое направление движения. Машинист поезда начинает движение со станции B и его первой остановкой будет станция С. На какой станции будет его 96 остановка?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 41.75 + 4 = 45.75
|
Между 6 станциями имеется 5 переездов (см. рис. в условии
задачи). Поэтому после каждых 5 × 2 = 10 переездов поезд будет находиться на исходной станции и двигаться в том же направлении. Следовательно, после 96 переездов поезд будет находиться на той же станции, что и после 6 переездов. 6 остановок после станции В в сторону станции С следующие: C – D – E – F – E – D. Итак, 96-я остановка будет на станции D.
Задание 15
|
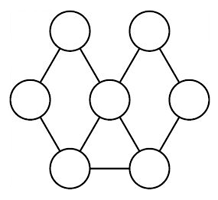
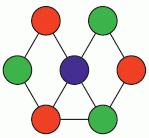
Катя хочет раскрасить круги на картинке так, чтобы любые два круга, соединённые отрезком, были окрашены в разные цвета. Какое наименьшее количество разных красок ей понадобится?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 45.75 + 4 = 49.75
|
Рассмотрим центральный кружок и два, расположенные под ним. Все эти 3 кружка соединены друг с другом отрезками. Поэтому никакие два из них не могут быть окрашены одинаковыми красками. Следовательно, понадобится не менее 3 различных красок. С другой стороны, 3 красок достаточно (см. рис.).
Задание 16
|
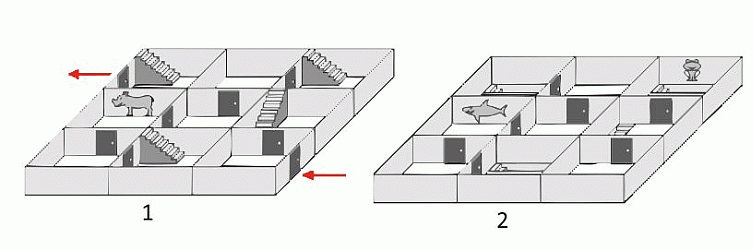
Семён идет по двухэтажному лабиринту от входа до выхода, минуя 3 стены с картинами. В каком порядке он эти картины увидит?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 49.75 + 4 = 53.75
|
Семён может пройти от входа до выхода только в порядке увеличения номеров комнат на следующем рисунке.
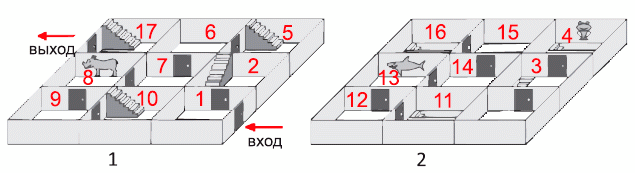
Поэтому сначала он увидит лягушку в комнате 4, затем – носорога в комнате 8 и, наконец, акулу в комнате 13.
Задание 17
|

6 бобров и 2 кенгуру стоят в ряд. Среди любых трёх последовательно пронумерованных животных ровно один кенгуру. Какое из следующих пронумерованных животных является кенгуру?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 53.75 - 1.25 = 52.5
|
Согласно условию, среди животных с номерами 1, 2, 3 ровно один кенгуру и среди животных с номерами 6, 7, 8 ровно один кенгуру. Также, по условию, в данном ряду только 2 кенгуру. Поэтому животные с номерами 4 и 5 – бобры. А тогда животные 3 и 6 должны быть кенгуру. Иначе три животных 3, 4, 5 или 4, 5, 6 будут бобрами, что противоречит условию задачи. Таким образом, среди вариантов ответа правильным является ответ В.
Задание 18
|
Галя, Боря и Рома всегда заходят в гостиную по очереди. Галя никогда не входит первой, Боря никогда не входит вторым, а Рома никогда не входит третьим. Сколько существует различных способов, которыми они могут войти в гостиную?
A) 1 Б) 2 В) 3 Г) 4 Д) 6
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 52.5 - 1.25 = 51.25
|
Согласно условию, есть две возможности: Галя входит второй или третьей. Если Галя входит второй, то Рома должен быть первым, а Боря – третьим. Если же Галя входит третьей, то Боря должен быть первым, а Рома – вторым. Видим, что существует ровно 2 способа, как Галя, Боря и Рома могут входить в гостиную.
Задание 19
|
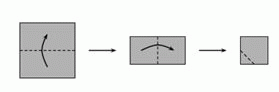
Вероника дважды складывает квадратный лист бумаги, как показано на рисунке. Затем она отрезает угол и разворачивает бумагу. Как выглядит лист бумаги в развёрнутом виде?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 51.25 + 5 = 56.25
|
После сворачивания данного листа нижняя левая вершина полученного квадрата – это центр исходного листа. Поэтому из каждой четверти исходного листа будет вырезан треугольник, одна из вершин которого – центр исходного листа. Следовательно, после разворачивания получится результат Б.
Задание 20
|
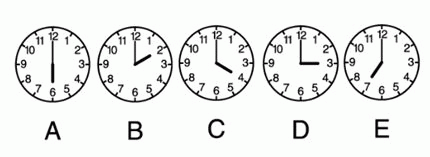
На стене висят пять часов. Известно, что какие-то часы на час спешат, какие-то - на час отстают, какие-то - показывают правильное время, и двое часов остановились. Какие часы показывают правильное время?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 56.25 + 5 = 61.25
|
Часы на рисунке в условии задачи показывают время: 6, 2, 4, 3 и 7 часов. При этом, по условию, среди них есть часы, которые идут точно, есть часы, которые на час опаздывают, и есть часы, которые на час спешат. Этим троим часам должны соответствовать три последовательных числа из пяти перечисленных. Есть только одна такая тройка: 2, 3, 4. Поэтому правильное время – это 3 часа. Такое время показывают часы Г) D.
Задание 21
|

У Адама и Вали по 9 шариков. Вместе у них 8 красных и 10 синих шариков. У Вали в два раза больше синих шариков, чем красных. Сколько синих шариков у Адама?
A) 3 Б) 4 В) 5 Г) 6 Д) 0
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 61.25 + 5 = 66.25
|
По условию, у Вали 9 шариков и среди них синих шариков в 2 раза больше, чем красных. Тогда у Вали 6 синих и 3 красных шарика. Поэтому у Адама 10 – 6 = 4 синих шарика.
Задание 22
|
У Лизы есть два аппарата. Когда Лиза кладёт квадратный лист бумаги в аппарат R, он поворачивает бумагу на 90° по часовой стрелке, как показано на рисунке. Когда Лиза кладёт бумагу в аппарат S, он штампует на бумаге символ  .
.
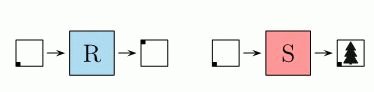
В каком порядке следует использовать аппараты для получения показанного ниже результата?
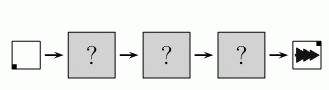
A) SRR Б) RSR В) RSS Г) RSS Д) SRS
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 66.25
На рисунке в условии задачи видно, что лист бумаги был повёрнут дважды и один раз был поставлен штамп. Штамп повёрнут один раз. Это может быть, только если после штампа сделан только один поворот, то есть штамп сделан вторым. Поэтому правильным является ответ Б) RSR.
|
Задание 23
|
Лена вписывает по одному из чисел от 1 до 7 в кружочки на рисунке, каждое ровно один раз. Она хочет, чтобы суммы чисел в двух соседних кружочках были такими, как указано на рисунке.
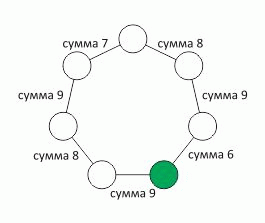
Какое число она должна вписать в зелёный кружочек?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 66.25
Числа во всех кружочках легко определяются после того, как найдено значение в каком-то одном из кружочков. Выясним, в каком кружочке должно быть записано наименьшее из данных чисел – число 1. Заметим, что обе суммы на отрезках, выходящих из данного кружочка, не превосходят
1 + 7 = 8.
На рисунке в условии задачи видно, что единственным кружочком, возле которого суммы меньше 9, – это самый верхний кружочек. В нём и должно быть число 1. Тогда в соседних с ним кружочках (слева направо) должны быть числа
6 = 7 – 1 и 7 = 8 – 1 соответственно.
Далее, соседние числа с найденными числами 6 и 7 – это, соответственно,
3 = 9 – 6 и 2 = 9 – 7.
Наконец, в двух нижних кружочках должны быть числа (слева направо)
5 = 8 – 3 и 4 = 6 – 2.
Таким образом, в зелёном кружочке должно быть число 4 (см. рис.).
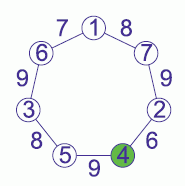
|
Задание 24
|
Маша закрасила ровно 5 клеток в таблице 4 × 4. Она предложила пяти своим друзьям угадать, какие клетки она закрасила. Нарисованные ими таблицы показаны ниже. Маша посмотрела на них и говорит: «Один из вас угадал все 5 клеток, а все остальные угадали ровно 4 клетки».
Какую таблицу нарисовала Маша?

|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 66.25 - 1.25 = 65
|
Укажем в каждой закрашенной клетке, сколько раз она закрашена во всех пяти таблицах.
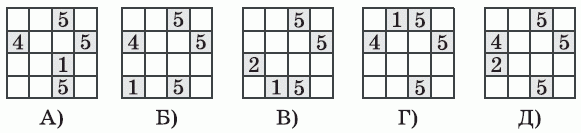
Видим, что три клетки закрашены во всех таблицах. Сравним расположения двух других клеток. Так как одна девочка угадала все 5 клеток, то её таблица совпадает с таблицей Марии. Остальные таблицы должны отличаться от этой таблицы только расположением одной клетки. Заметим, что таблица В) отличается от каждой из таблиц А), Б) и Г) расположением двух окрашенных клеток. Поэтому все эти 4 таблицы не являются искомыми. Таким образом, правильным может быть только ответ Д). Сравнивая таблицу в этом ответе с каждой из первых четырёх таблиц, убеждаемся, что каждый раз имеется по 4 одинаково расположенные окрашенные клетки. Итак, правильный ответ – ответ Д).



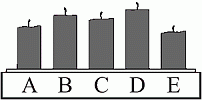
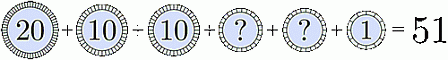









 поверх чёрного круга соответствующего размера
поверх чёрного круга соответствующего размера  .
.
















 .
.





