Задание 1
|
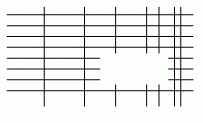
На схеме показан набор горизонтальных и вертикальных линий с удалённой частью. Какой из следующих является удалённая часть?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Дорисуем удалённые части отрезков (см. рис.).
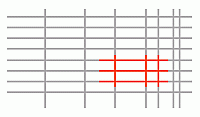
Видим, что удалённым является фрагмент Д.
Задание 2
|
Какая из следующих фигур не может быть разрезана по прямой линии на две трапеции?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 33 + 3 = 36
|
Один прямолинейный разрез многоугольника на две части увеличивает число вершин не более чем на 4. Поэтому части, которые получатся после разрезания треугольника, имеют не более 3 + 4 = 7 вершин. А две трапеции вместе имеют 8 вершин. Следовательно, треугольник разрезать на две трапеции нельзя. Фигуры в других вариантах ответа на две трапеции разрезать можно (см. рис.).

Задание 3
|
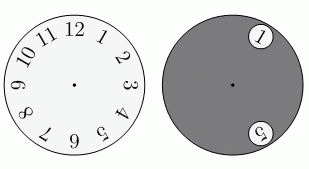
Серый круг с двумя отверстиями наложили сверху на циферблат, как показано на рисунке. Его повернули вокруг центра так, что в одном из отверстий оказалось число 8. Какие из следующих чисел можно увидеть в другом отверстии?
A) 4 или 12
Б) 1 или 5
В) 1 или 4
Г) 7 или 11
Д) 5 или 12
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 36 + 3 = 39
|
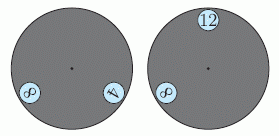
На рисунке в условии задачи видно, что разница между числами в отверстиях серого круга равна 4. Ясно, что это соотношение сохраняется при поворотах данного круга (с некоторой поправкой, если одно из отверстий при повороте минует число 12 или окажется на нём). Поэтому, если в одном из отверстий оказалось число 8, то в другом будет либо 8 – 4 = 4, либо 8 + 4 = 12 (см. также рис.).
Задание 4
|
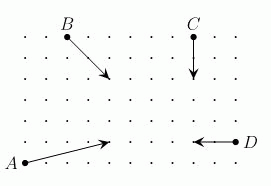
На рисунке показано начальное положение, направление движения и расстояние, которое четыре бамперных машинки на аттракционе проезжают за пять секунд. Какие две машинки столкнутся?
A) A и В
Б) А и С
В) А и D
Г) В и С
Д) С и D
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Проведём стрелки, показывающие месторасположение машинок через следующие 5 секунд (см. рис.).
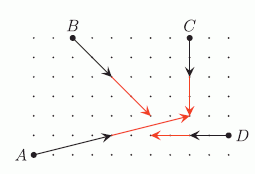
Видим, что машинки А и С столкнутся через 10 секунд. Никакая другая пара машинок не столкнётся.
Задание 5
|
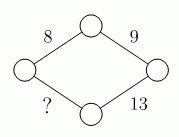
Витя хочет записать числа в вершинах и на сторонах ромба так, чтобы число на стороне равнялось сумме чисел на его концах. Какое число должно быть записано вместо знака вопроса?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
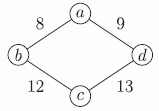
Заметим, что суммы двух чисел на любых двух противоположных рёбрах одинаковы. Действительно, если, например, в вершинах вписаны числа a, b, c, и d, то на одной паре противоположных рёбер сумма чисел будет равна
(a + b) + (c + d) = a + b + c + d,
на другой паре противоположных рёбер сумма чисел будет равна
(a + d) + (b + c) = a + b + c + d.
Следовательно, на ребре со знаком «?» должно быть записано число
8 + 13 – 9 = 12.
Задание 6
|
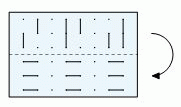
У Кристины есть прозрачный лист с нарисованными отрезками. Кристина сложила лист по пунктирной линии. Что она теперь может видеть?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 37.5 + 3 = 40.5
|
После сгибания вертикальные отрезки отобразятся на нижнюю часть листа симметрично относительно пунктирной линии (см. рис.). Поэтому получим результат
в ответе В.
Задание 7
|
Каменщик хочет выложить пол 4 × 6 одинаковыми плитками. Зазоры и пропуски не допускаются. Какие из следующих плиток для это НЕЛЬЗЯ использовать?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Согласно условию задачи, площадь пола равна
4 · 6 = 24 (кв. ед.).
Плитки вида Г) имеют площадь 5 (кв. ед.). Но 24 не делится на 5. Поэтому плитками Г) пол выложить нельзя. А плитками, указанными в других вариантах ответа, выложить данный пол можно (см. рис.).

Задание 8
|
У Вани есть 150 монет. Когда он бросил монеты на стол, 40% из них выпали орлом, а 60% — решкой. Сколько монет, на которых выпала решка, нужно перевернуть, чтобы число решек и орлов было одинаковым?
A) 10 Б) 15 В) 20 Г) 25 Д) 30
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Согласно условию, 150 · 0,4 = 60 монет выпали орлом и 150 · 0,6 = 90 – решкой. Половина от числа всех монет равна 150 : 2 = 75. Поэтому число монет, выпавших орлом, надо увеличить на 75 – 60 = 15, а число монет, выпавших решкой, уменьшить на 90 – 75 = 15. Видим, что нужно перевернуть 15 монет, выпавших решкой.
По-другому правильный ответ можно найти так. Чтобы орлов и решек было поровну, нужно перевернуть 10% от общего числа монет (тех, которые лежат решкой). Тогда число орлов увеличится на 10%, а число решек уменьшится на 10%. В результате и тех, и других станет по 50%, что и требуется. Далее, 10% от 150 – это 150 · 0,1 = 15.
Задание 9
|
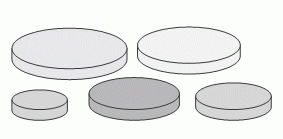
У Ани есть пять круглых дисков разного размера. Она хочет построить башню из трёх дисков так, чтобы под каждым диском был диск большего размера. Сколько разных башен может построить Аня?
A) 5 Б) 6 В) 8 Г) 10 Д) 15
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 46.5 - 0.75 = 45.75
|
Пронумеруем диски числами от 1 до 5 в порядке возрастания их радиуса. Тогда «построить башню» так, как требуется в условии, означает выбрать три из данных чисел и расположить их в порядке возрастания. Так как все числа различны, то расположить любые три из них в порядке возрастания можно только одним способом. Поэтому число башен равно числу способов выбрать 3 числа из 5. Это число равно числу способов удалить 2 числа из 5. Для тех, кто знаком с комбинаторикой, оно равно числу сочетаний
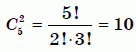
Поскольку это число небольшое, все способы удалить 2 числа из 5 можно выписать и подсчитать непосредственно:
(1, 2); (1, 3); (1, 4); (1, 5); (2, 3); (2, 4); (2, 5); (3, 4); (3, 5); (3, 5).
Видим, что число таких пар равно 10.
Задание 10
|
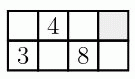
Ева хочет вписать числа от 1 до 8 в клетки таблицы, так чтобы суммы чисел во всех строчках были равными, и суммы чисел во всех столбцах также были равными. Она уже вписала числа 3, 4 и 8, как показано на рисунке. Какое число ей следует вписать в правую верхнюю клетку?
A) 1 Б) 2 В) 5 Г) 6 Д) 7
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 45.75 - 0.75 = 45
|
Сумма всех чисел от 1 до 8 равна
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
Поэтому сумма чисел в каждом из 4 столбцов должна быть равна
36 : 4 = 9.
В результате легко определяются числа в пустых клетках первых трёх столбцов (см. рис. 1).
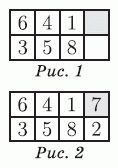
Далее, сумма чисел в каждой строчке должна быть равна
36 : 2 = 18.
С учётом этого находим числа в правых клетках строчек (см. рис. 2). Видим, что правильным является ответ 7.
Задание 11
|
Тамара записала три последовательных трёхзначных натуральных числа, затем она цифры заменила символами (одинаковые цифры – одинаковыми символами, а разные – разными). У неё получилось:
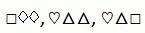
Как в этих символах запишется следующее по величине число?
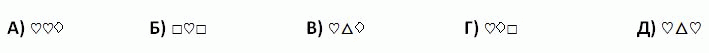
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 45 + 4 = 49
|
Так как после добавления 1 к первому числу получаем второе число, у которого изменилась первая цифра, то ◊ = 9, а △ = 0 и тогда, так как третье число на 1 больше второго, □ = 1. Таким образом, первое число – это 199. Тогда второе число – 200 и, значит, ♡ = 2. Тогда четвёртым должно быть число 202, которое в применяемых символах запишется как ♡△♡.
Задание 12
|
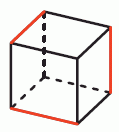
Некоторые рёбра куба окрашены в красный цвет так, что на каждой грани есть хотя бы одно красное ребро. Какое наименьшее число красных рёбер может быть у такого куба?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 49 - 1 = 48
|
Куб имеет 6 граней. Каждое ребро принадлежит ровно двум граням. Поэтому число окрашенных рёбер не может быть меньше 6 : 2 = 3. С другой стороны, 3 ребра окрасить так, как требуется в условии задачи, можно (см. рис.).
Задание 13
|
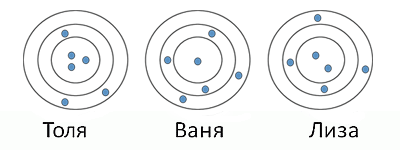
Толя, Ваня и Лиза выпустили по шесть стрел в цель. Стрелы, попадающие в любое место внутри одного кольца, приносят одинаковое количество очков. Толя набрал 46 очков, Ваня — 34 очка. Сколько очков набрала Лиза?
A) 37 Б) 38 В) 39 Г) 40 Д) 41
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 48 - 1 = 47
|
Заметим, что если в каждом кольце сложить вместе все попадания Толи и Вани, то их будет ровно в два раза больше, чем количество попаданий Лизы. Следовательно, Лиза набрала
(46 + 34) : 2 = 40 очков.
Задание 14
|
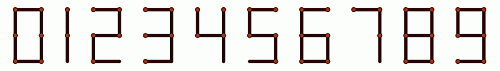
Из спичек можно составлять числа так, как показано на рисунке. Например, для составления числа 14 требуется 6 спичек. Сколько различных натуральных чисел можно составить ровно из 6 спичек?
A) 2 Б) 4 В) 6 Г) 8 Д) 9
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 47 - 1 = 46
|
Ровно из 6 спичек состоят цифры 0, 6 и 9. Т.к. число должно быть положительным, то 0 не подходит. То есть из 6 спичек можно составить 2 однозначных числа. Наименьшее число спичек – 2 спички – имеет число 1. Количество 6 – 2 = 4 спичек имеет только цифра 4. Поэтому можно составить двузначные числа 14 и 41. Из 3 спичек состоит цифра 7. Это даёт ещё одно двузначное число – 77.
Единственным трёхзначным числом из 6 спичек является число 111.
Других чисел из 6 спичек составить нельзя. Таким образом, всего существует 6 чисел, которые можно составить из 6 спичек.
Задание 15
|
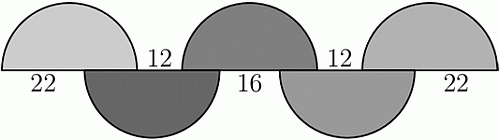
На рисунке показаны пять равных полуокружностей и длины некоторых отрезков. Чему равен радиус полуокружностей?
A) 12 Б) 16 В) 18 Г) 22 Д) 36
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 46 + 4 = 50
|
Пусть r – радиус полуокружностей. Подсчитаем двумя способами расстояние между крайними точками отрезка, на котором расположены диаметры данных полуокружностей. Получим уравнение
2r + 12 + 2r + 12 + 2r = 22 + 2r + 16 + 2r +22, или
6r + 24 = 4r + 60, или
2r = 36, откуда
r = 18.
Задание 16
|
Стороны квадрата имеют длину 1 см. Сколько точек на плоскости этого квадрата находятся на расстоянии ровно 1 см от двух его вершин?
A) 4 Б) 6 В) 8 Г) 10 Д) 12
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 50 - 1 = 49
|
Существует 6 способов выбора двух вершин квадрата. Это либо 2 вершины на одной стороне квадрата, либо 2 вершины на одной диагонали. Каждый раз по обе стороны как от диагонали квадрата, так и от стороны квадрата, на их серединных перпендикулярах находится по одной точке, удалённой от концов данных отрезков на расстоянии 1 см. Получаем 6 · 2 = 12 искомых точек. Среди них нет совпадающих (см. рис.).
Задание 17
|
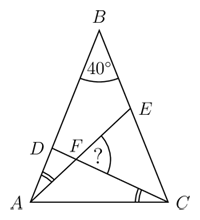
Треугольник ABC равнобедренный, ∠ABC = 40°. Два отмеченных угла ∠EAB и ∠DCA равны. Какова величина угла ∠CFE ?
A) 55° Б) 60° В) 65° Г) 70° Д) 75°
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 49 + 4 = 53
|
Поскольку треугольник ABC равнобедренный и угол при вершине В равен 40°, то углы при основании
∠ BCA = ∠ CAB = (180 − 40) : 2 = 70°.
Пусть ∠ EAB = ∠ DCA = α. Тогда в ΔFAC внешний угол
∠ EFC = ∠ FAC + ∠ FСA = (70° − α) + α = 70°.
Задание 18
|
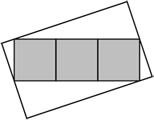
На рисунке показан прямоугольник, составленный из трёх серых квадратов площадью 25 см2 каждый, расположенных внутри большего белого прямоугольника. Две вершины серого прямоугольника являются серединами коротких сторон белого прямоугольника, а две другие вершины серого прямоугольника лежат на двух других сторонах белого прямоугольника. Чему равна площадь белого прямоугольника?
A) 125 см2 Б) 136 см2 В) 149 см2 Г) 150 см2 Д) 172 см2
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 53 - 1 = 52
|
По условию, левая нижняя и правая верхняя вершины серого прямоугольника являются серединами соответствующих сторон белого прямоугольника. Поэтому, отразив все четыре прямоугольных треугольника (части белого прямоугольника, не покрытые серым прямоугольником) относительно их гипотенуз, мы получим фигуру, в точности совпадающую с серым прямоугольником (см. рис.).
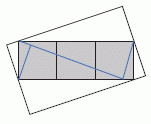
Следовательно, площадь белого прямоугольника в 2 раза больше площади серого прямоугольника и, значит, она равна
2 · (3 · 25) = 150 см2.
Задание 19
|
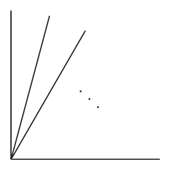
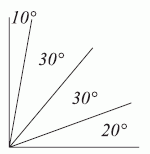
Два луча образуют прямой угол. Какое наименьшее число лучей нужно ещё провести внутри этого угла, чтобы для любого из значений 10°, 20°, 30°, 40°, 50°, 60°, 70° и 80°, нашлись два луча, угол между которыми равен данному значению?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 52 - 1 = 51
|
Ясно, что двух дополнительных лучей недостаточно. Действительно, из 4 лучей можно составить только 6 различных пар и, значит, можно получить не более 6 различных углов. Пример на рисунке показывает, что трёх лучей достаточно.
Задание 20
|
Сумма 2023-х последовательных целых чисел равна 2023. Какова сумма цифр самого большого из этих чисел?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 51 - 1 = 50
|
Понятно, что среди данных последовательных чисел есть отрицательные, иначе их сумма была бы заведомо больше 2023. Рассмотрим 2023 последовательных числа от –1011 до 1011. Их сумма равна 0. Сдвинем ряд этих чисел вправо, т.е. увеличим все числа на 1. Получим ряд чисел от –1010 до 1012. Легко видеть, что их сумма равна 1011 + 1012 = 2023. Следовательно, этот ряд чисел и есть тот, о котором говорится в условии задачи. Наибольшее число в этом ряду – число 1012. Сумма его цифр равна
1 + 0 + 1 + 2 = 4.
Задание 21
|
По кругу стоят три бобра и несколько кенгуру. При этом никакие два бобра не стоят рядом, но есть стоящие подряд три кенгуру. Какое наименьшее число кенгуру может быть в этом кругу?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 50 + 5 = 55
|
По условию, 3 кенгуру (К) стоят между двумя бобрами (B). Поэтому часть круга – это последовательность BKKKB.
Так как никакие два бобра не стоят рядом и есть ещё один (третий) бобёр, то должно быть ещё по крайне мере два кенгуру: KBKKKBK. Видим, что число кенгуру не меньше 5. С другой стороны, если замкнуть круг, поставив бобра между крайними кенгуру в полученной последовательности, то все условия будут выполнены. Следовательно, правильным является ответ 5.
Задание 22
|
Миша стоит в очереди. Он заметил, что перед ним стоит столько же людей, сколько и позади него, и что число людей в очереди кратно 3. Миша видит также позади себя в очереди двух своих друзей, одного на 19 месте, а другого на 28 месте. Какое место в очереди занимает Миша?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 55 + 5 = 60
|
Пусть n человек стоят впереди Миши и n – позади. Тогда всего в очереди стоят 2n + 1 человек. По условию, n + 1 < 19, откуда n < 18. Кроме того, согласно условию, 2n + 1 ≥ 28, откуда n ≥ 13,5. Поэтому n может принимать только значения 14, 15, 16 или 17. Кроме того, по условию, 2n + 1 кратно 3. Тогда n = 16. Поэтому место в очереди, на котором находится Миша, равно n + 1 = 17.
Задание 23
|
Белоснежка организовала шахматный турнир для семи гномов. В турнире каждый гном должен сыграть по одной партии с каждым другим гномом. В понедельник первый гном сыграл 1 партию, второй - 2 партии, третий - 3, четвёртый - 4, пятый - 5, а шестой - 6. Сколько партий в это день сыграл седьмой гном?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 60 - 1.25 = 58.75
|
Построим граф, который показывает, сколько и каких партий сыграли гномы в понедельник. Гномов изобразим в виде вершин с соответствующими номерами. Так как шестой гном сыграл 6 партий, то это значит, что он сыграл со всеми остальными гномами. Соединим вершину 6 рёбрами со всеми остальными вершинами (см. рис.1).
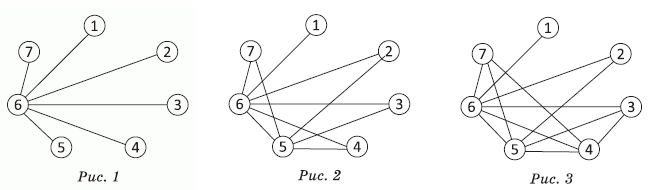
Видим, что та единственная партия, которую сыграл первый гном, была сыграна с шестым гномом. Поэтому пятый гном не играл с первым. Следовательно, все его партии были сыграны с другими пятью гномами (всеми, кроме первого). Проведём соответствующие рёбра, которые ещё не построены (см. рис.2). Далее, все партии первого и второго гномов уже определены. Поэтому два недостающих ребра, указывающих партии четвёртого гнома, – это рёбра к 3-й и 7-й вершинам. Дорисовав соответствующие 2 ребра, получим граф, описывающий все партии, сыгранные в понедельник (см. рис.3). На графе видим, что седьмой гном сыграл 3 партии.
Задание 24
|
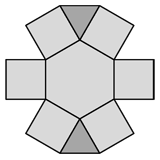
Лиза хочет вписать числа от 1 до 9 в многоугольники, из которых состоит фигура на рисунке, так, чтобы произведение чисел в любых двух соседних по стороне частях фигуры было не больше 15. Сколькими способами это можно сделать?
A) 12 Б) 8 В) 32 Г) 24 Д) 16
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 58.75 - 1.25 = 57.5
|
Заметим, что у чисел 8 и 9 не может быть больше одного соседнего числа и этим соседним числом может быть только число 1. Поэтому числа 1, 8 и 9 должны располагаться в областях 1, 8 и 9 на рисунке. При этом число 1, однозначно, должно быть в центре, 8 и 9 можно поменять местами.
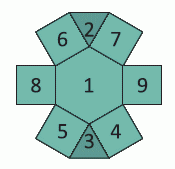
То есть имеется 2 способа расположения этих трёх чисел. Далее, числа 7 и 6 могут быть соседними только с числом 2. Есть 4 способа, как их расположить (число 2 в одном из треугольников, а числа 7 и 6 – двумя способами в соседних квадратах). Наконец, видим, что числа 5 и 4 могут быть соседними только с числом 3. Число 3, однозначно, располагается в треугольнике, не занятом числом 2. Числа 5 и 4 могут двумя способами расположиться в соседних квадратах. Таким образом, существует
2 · 4 · 2 = 16 способов разместить числа от 1 до 9 так, чтобы выполнялись условия задачи.
Задание 25
|
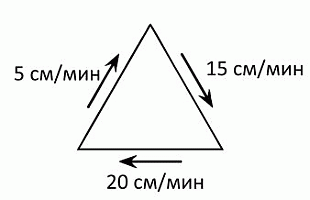
Муравей ходит по сторонам равностороннего треугольника. На рисунке указаны скорости, с которыми он перемещается по соответствующим сторонам. С какой средней скоростью в см/мин муравей обходит весь периметр треугольника?
A) 10 Б) 80/11 В) 180/19 Г) 15 Д) 40/3
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 57.5 - 1.25 = 56.25
|
Пусть сторона треугольника равна а см, тогда его периметр равен 3а см. Согласно условию, время обхода всего периметра треугольника равно
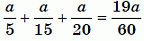 мин.
мин.
Тогда средняя скорость обхода равна
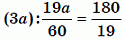 см/мин.
см/мин.
Задание 26
|
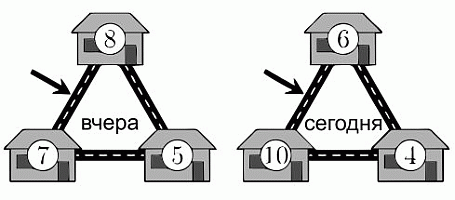
В трёх соседних домах живут несколько мышей. Прошлой ночью каждая мышь ушла из своего дома в какой-то из соседних домов. Числа на рисунке показывают количество мышей в домах вчера и сегодня. Сколько мышей прошли в ту или другую сторону по пути, обозначенному стрелкой?
A) 9 Б) 11 В) 12 Г) 15 Д) 16
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 56.25 - 1.25 = 55
|
Первое решение.
В верхнем и левом домах было 8 + 7 = 15 мышей. Все они перешли в другие дома. Некоторые
из них поменялись домами, другие перешли в третий (правый) дом. На втором рисунке мы видим, что в этот третий дом пришли 4 мыши. Это значит, что остальные, а именно 15 – 4 = 11 мышей, поменялись домами, т.е. прошли по указанному пути.
Второе решение.
Пусть x мышей перешло из верхнего дома в левый и y мышей перешло из левого дома в верхний. Нужно найти значение x + y. Согласно условию, 8 – x и 7 – y мышей перешли в третий домик (правый нижний). Далее, по условию,
(8 – x) + (7 – y) = 4, т.е.
15 – (x + y) = 4, откуда
(x + y) = 11.
Задание 27
|

Боря представил число 1015 как сумму чисел, в записи которых используются только цифры 7. Как видно на рисунке, всего он использовал эту цифру 10 раз. Теперь он хочет представить число 2023 в виде суммы чисел, используя только цифру 7 ровно 19 раз. Сколько слагаемых в такой сумме будут равны 77?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 55 - 1.25 = 53.75
|
Первое решение.
Поскольку цифра единиц в сумме, полученной после сложения чисел, составленных из цифр 7, равна 3, то таких слагаемых 9 (7 · 9 = 63). Если больше, то их должно быть 19, т.е. все слагаемые однозначные. Но их сумма
7 · 19 ≠ 2023.
Далее, так как 7 · 9 = 63, из разряда единиц в разряд десятков будет перенесена цифра 6. Чтобы при суммировании цифра десятков стала равна 2, необходимо 8 семёрок в разряде десятков (7 · 8 = 56).
Так как 8 · 70 + 9 · 7 = 623, то число семёрок в разряде сотен равно
(2023 – 623) : (7 · 100) = 1400 : 700 = 2.
Итак, в искомой сумме имеется 2 трёхзначных числа, 9 – 8 = 1 однозначное число и, значит, 9 – 2 – 1 = 6 двузначных чисел.
Второе решение.
Ясно, что все слагаемые нужной суммы не более чем трёхзначные. Трёхзначных слагаемых меньше 3, поскольку
3 · 777 = 2331 > 2023.
Кроме того, одного слагаемого 777 недостаточно, так как
(2023 – 777) : 77 > 16.
Но в таком случае число цифр 7 будет заведомо больше 19, что противоречит условию задачи. Итак, в данной сумме два слагаемых 777. Тогда сумма двузначных и однозначных слагаемых равна
2023 – 2 · 777 = 469.
Кроме того, количество цифр 7 в этих числах равно
19 – 2 · 3 = 13.
Это значит, что слагаемых 77 не более шести. И это количество подходит, так как
77 · 6 + 7 = 469.
Если же количество слагаемых 77 меньше шести, то и сумма двузначных и однозначных слагаемых будет меньше 469. Поэтому правильным является ответ 6.
Задание 28
|
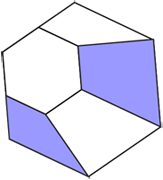
Правильный шестиугольник разрезали на четыре четырехугольника и один меньший правильный шестиугольник, как показано на рисунке. Площадь окрашенной части относится к площади меньшего шестиугольника как 4 : 3. Как относится площадь малого шестиугольника к площади большого шестиугольника?
A) 3 : 11
Б) 1 : 3
В) 2 : 3
Г) 3 : 4
Д) 3: 5
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 53.75 + 5 = 58.75
|
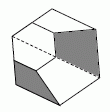
Штриховая линия на рисунке является линией симметрии данного шестиугольника. Видим, что окрашенные и неокрашенные четырёхугольники соответственно равны. Поэтому, если площадь большого шестиугольника равна S, а площадь меньшего шестиугольника равна s, то площадь окрашенной части равна
(S – s) : 2.
Согласно условию задачи,
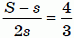 ,
,
откуда 3S – 3s = 8s,
или 3S = 11s,
откуда s : S = 3 : 11.
Задание 29
|

Женя написал шесть последовательных натуральных чисел на шести листочках бумаги, по одному числу на каждом листочке. Затем он приклеил эти листочки сверху и снизу на сторонах трёх монет. Затем он трижды подбросил эти три монеты. При первом броске выпали числа 6, 7 и 8. При втором броске сумма выпавших чисел оказалась равна 23, а при третьем броске - 17. Какова сумма чисел, не выпавших при первом броске?
A) 18 Б) 19 В) 23 Г) 24 Д) 30
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 58.75 - 1.25 = 57.5
|
Если среди последовательных шести чисел есть числа 6, 7, 8, то есть только четыре возможности:
1) этими числами являются числа от 3 до 8;
2) числа от 4 до 9;
3) числа от 5 до 10;
4) числа от 6 до 11.
Сумму 24 не дают никакие три числа в случае 1), так как в этом случае наибольшая сумма трёх чисел равна
6 + 7 + 8 = 21 < 24.
Сумму 17 не дают никакие три числа в случае 3), так как в этом случае наименьшая сумма трёх чисел равна
5 + 6 + 7 = 18 > 17.
В случае 4) все числа больше, чем в 3), и, значит, сумму 17 также нельзя получить.
Поэтому числами, которые записал Женя, могут быть только числа от 4 до 9. Следовательно, сумма чисел, не выпавших
после первого броска, равна
4 + 5 + 9 = 18.
Задание 30
|
Команда по регби набрала 24, 17 и 25 очков в седьмой, восьмой и девятой играх сезона 2022 года. Среднее количество очков за игру после 9 игр оказалось больше, чем после первых 6 игр. Среднее количество очков после 10 игр составило более 22. Какое наименьшее количество очков могла набрать команда в своей десятой игре?
A) 22 Б) 23 В) 24 Г) 25 Д) 26
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 57.5 - 1.25 = 56.25
|
Среднее значение в седьмой, восьмой и девятой играх равно
(24 + 17 + 25) : 3 = 66 : 3 = 22.
Тогда из условия следует, что среднее значение после первых 6 игр было меньше 22. То есть за первые 6 игр команда могла набрать не более
22 · 6 – 1 = 131 очка.
После 10 игр среднее значение должно быть больше 22. Поэтому всего за 10 матчей команда должна набрать не менее
10 · 22 + 1 = 221 очка.
Тогда наименьшее число очков, которое могло быть набрано в последнем матче, равно
221 – 131 – 66 = 24.
Это значение достигается. Например, если в играх от первой до десятой были набраны соответственно очки 21, 22, 22, 22, 22, 22, 24, 17, 25, 24, то среднее значение числа очков за первые 6 игр равно
(21 + 22 · 5 ) : 6 = 131 : 6 = 21,8(3).
Среднее значение за первые 9 игр равно
(131 + 24 + 17 + 25) : 9 = 197 : 9 = 21,8(8),
а среднее значение после всех 10 игр равно
(197 + 24) : 10 = 22,1.
Видим, что все условия задачи выполняются. Поэтому правильным является ответ 24.




















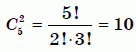


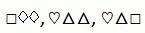
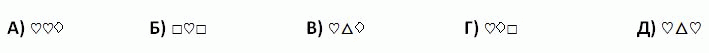














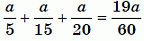 мин.
мин.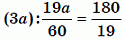 см/мин.
см/мин.



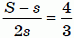 ,
,
