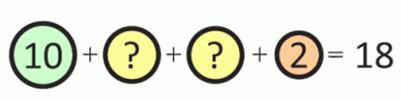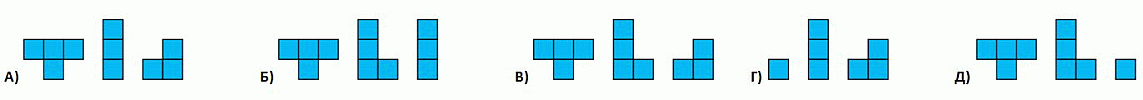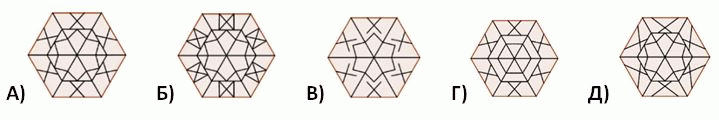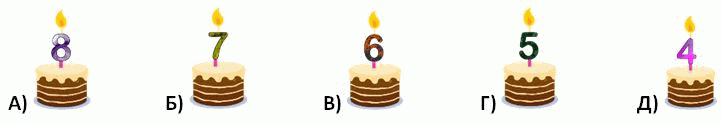Задание 1
|

Сколько кругов на рисунке?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 24 + 3 = 27
|
Внутри жёлтого круга находятся ещё 3 круга (см. рис.). Всего их 4. Внутри двух голубых кругов находится ещё по одному кругу. Всего их также 4. Итого: на рисунке 4 + 4 = 8 кругов.
Задание 2
|
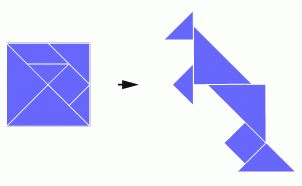
Квадрат разрезали на фигурки, как показано на рисунке. Боря сложил из полученных фигурок кенгуру. Но одна фигурка осталась. Какая?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 27 + 3 = 30
|
Кенгуру на рисунке состоит из 5 треугольников разных размеров и квадрата. Следовательно, у Бори осталась фигурка А).
Задание 3
|
На рисунке моей лодки более 1 круга, а треугольников на 2 больше, чем квадратов. На каком из следующих рисунков изображена моя лодка?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 30 - 0.75 = 29.25
|
По условию, на моей лодке более 1 круга. Поэтому ответ В
не является верным (см. рис. в условии задачи). Далее, по условию, разность между числом треугольников и числом квадратов на парусе мой лодки должна быть равна 2. Подсчитаем такие разности в четырёх оставшихся вариантах ответа. Получим
А) 2 – 1 = 1;
Б) 3 – 2 = 1;
Г) треугольников меньше, чем квадратов;
Д) 4 – 2 = 2.
Таким образом, правильным является ответ Д.
Задание 4
|
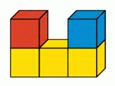
На рисунке показаны 5 кубиков. Что мы увидим, если посмотрим на них сверху?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Крайние верхние кубики – красный и синий (см рис.). Они будут видны сверху. Выше среднего жёлтого кубика в нижнем ряду нет кубиков. Поэтому этот жёлтый кубик будет виден сверху. Следовательно, правильным является ответ Б.
Задание 5
|
В каждой чаше на следующих рисунках находятся шарики с числами. В какой чаше сумма чисел на всех шариках наибольшая?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Можно непосредственно подсчитать суммы чисел во всех вариантах ответа. Получим:
А) 8 + 7 + 4 + 9 = 28;
Б) 4 + 6 + 7 + 9 = 26;
В) 7 + 9 + 4 + 7 = 27;
Г) 9 + 7 + 4 + 4 = 24;
Д) 7 + 4 + 9 + 5 = 25.
Сравнивая результаты, видим, что наибольшая сумма 28 – сумма в ответе А. Он и является правильным.
Но правильный ответ можно найти и без вычисления сумм. Заметим, что во всех чашах есть по три шарика с одинаковыми числами: 9, 7 и 4. Поэтому сумма будет наибольшей в той чаше, в которой число у четвёртого шарика наибольшее. Такое число – число 8 у четвёртого
шарика в чаше А.
Задание 6
|

Моему дедушке на день рождения приготовили торт. Свечи на торте показывают, сколько лет ему исполнилось. Высокая свеча означает 10 лет, а низкая – 1 год. Сколько лет исполнилось моему дедушке?
A) 65 Б) 66 В) 76 Г) 77 Д) 78
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 35.25 + 3 = 38.25
|
На рисунке в условии задачи 7 высоких свечей и 6 низких. Поэтому, согласно условию, дедушке исполнилось
7 × 10 + 6 = 76 лет.
Задание 7
|
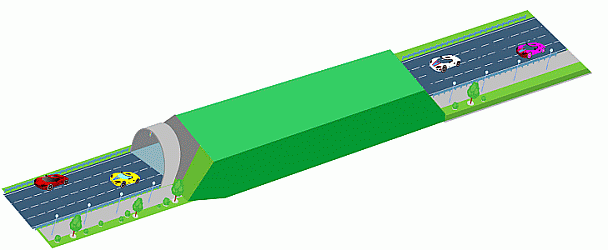
По трассе движутся 10 автомобилей. Те из них, которые не видны на рисунке, находятся в туннеле. Сколько автомобилей в туннеле?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
На рисунке в условии задачи мы видим 2 автомобиля слева от туннеля и 2 – справа от него. Всего их
2 + 2 = 4.
Следовательно, в туннеле
10 – 4 = 6 автомобилей.
Задание 8
|
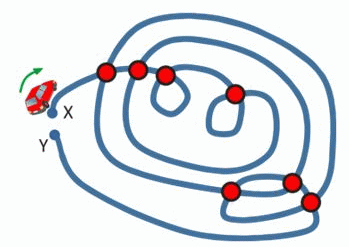
Стёпа проехал из X в Y, как показано на рисунке. На каждом перекрёстке он останавливался, прежде чем двигаться прямо. Сколько всего раз он останавливался?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
На рисунке в условии задачи отмечены 7 перекрёстков (красных кружочков). Заметим, что каждый перекрёсток автомобиль пересёк 2 раза. По условию, перед пересечением он каждый раз останавливался. Поэтому всего по пути автомобиль совершил
7 × 2 = 14 остановок.
Задание 9
|
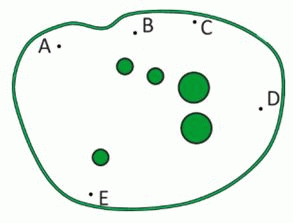
В парке 5 деревьев. Бобёр видит только два дерева, потому что все остальные скрыты за другими деревьями. В какой из отмеченных точек сидит бобёр?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.5 + 4 = 44.5
|
Из точки D видны только 2 ближайших крупных дерева. Остальные деревья скрыты за ними. Из точек A, B, C можно видеть по 3 дерева, а из точки Е – 4 дерева. По условию, бобёр видит только 2 дерева. Значит, он сидит в точке D.
Задание 10
|
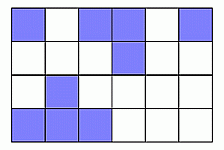
Лист бумаги разбит на 24 клетки. Соня окрасила некоторые из клеток, как показано на рисунке. Сколько ещё клеток ей нужно окрасить, чтобы были окрашены половина всех клеток?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 44.5 + 4 = 48.5
|
Половина от 24 клеток – это
24 : 2 = 12 клеток.
На рисунке окрашено
1 + 4 + 3 + 1 = 9 клеток.
Поэтому Соне нужно окрасить ещё
12 – 9 = 3 клетки.
Задание 11
|
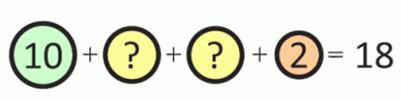
На рисунке на двух жетонах со знаком вопроса записаны одинаковые числа. Что это за числа, если сумма чисел на всех четырёх жетонах равна 18?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 48.5 + 4 = 52.5
|
Согласно условию, сумма чисел на двух жетонах со знаком «?» равна
18 – 10 – 2 = 6.
Поэтому число на одном жетоне со знаком «?» равно
6 × 2 = 3.
Задание 12
|
Рая рисует пчелу

Ей нужно добавить ещё несколько элементов, чтобы получить

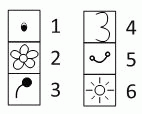
Чему равна сумма номеров этих элементов?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 52.5 - 1 = 51.5
|
Для завершения рисунка не хватает четырёх элементов. Их номера: 1 (глаз); 3 (антенна); 4 (правые крылья) и 5 (рот). Сумма этих номеров равна
1 + 3 + 4 + 5 = 13.
Задание 13
|

В таблице 30 клеток. Все клетки 3 и 6 строчек и все клетки столбцов C и D закрасили. Сколько клеток остались незакрашенными?
A) 8 Б) 10 В) 12 Г) 18 Д) 22
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 51.5 + 4 = 55.5
|
Окрасим клетки указанных в условии строчек и столбцов (см. рис.).
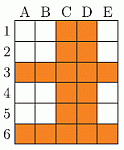
После этого легко подсчитать, что не окрашены 12 клеток.
По-другому ответ можно найти так. Если окрашены 2 строчки, то остались
6 – 2 = 4 строчки, окрашенные не полностью.
Если после этого ещё окрашены 2 столбца, то в этих 4-х строчках остаётся по
5 – 2 = 3 неокрашенные клетки, т.е. всего
4 × 3 = 12 неокрашенных клеток во всей таблице.
Задание 14
|
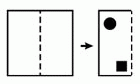
Лист бумаги согнули пополам и сделали два отверстия: круглое и квадратное. Как будет выглядеть этот лист, если его развернуть обратно?

|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 55.5 - 1 = 54.5
|
Развёрнут лист будет по штриховой линии. Поэтому два квадратных отверстия окажутся ближайшими к штриховой линии, а два круглых отверстия – наиболее удалёнными от неё. Таким условиям удовлетворяет только ответ Б.
Задание 15
|
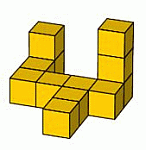
Вася склеил фигуру из 12 кубиков. Для склеивания любых двух соседних кубиков ему понадобилась одна капля клея. Сколько всего капель клея израсходовал Вася?
A) 8 Б) 9 В) 10 Г) 11 Д) 12
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 54.5 + 4 = 58.5
|
У фигуры, которую склеил Вася, 3 кубика имеют только по 1 соседнему кубику (с которым они склеены), 1 кубик – 3 соседних, остальные 8 кубиков – по 2 соседних. Поэтому всего склеено
1 + 1 + 1 + 3 × 1 + 8 × 2 = 22 грани.
По условию, на склеивание двух соседних граней ушла 1 капля клея. Следовательно, всего Вася израсходовал
22 : 2 = 11 капель клея.
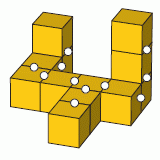
По-другому ответ можно получить, непосредственно отметив на рисунке по одному ребру тех граней, которые были склеены (см. рис.).
Задание 16
|
Максим складывает квадрат из клетчатых фигурок.

У него остались ещё фигурки:
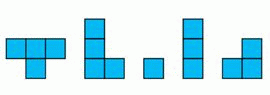
Какие из них понадобятся для завершения работы?
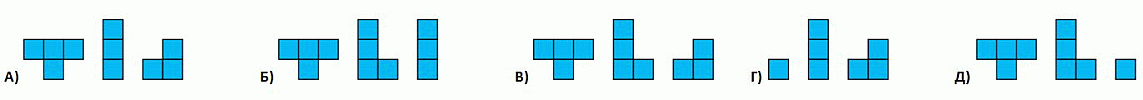
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 58.5 + 4 = 62.5
|
В квадрате остаются пустыми 10 клеток. В совокупности
10 = 4 + 3 + 3 клеток имеют фигуры только в ответе А.
В других ответах число клеток:
Б) 4 + 4 + 3 = 11,
В) 4 + 4 + 3 = 11,
Г) 1 + 3 + 3 = 7,
Д) 4 + 4 + 1 = 9.
Поэтому правильным может быть только ответ А. На рисунке показано, что, действительно, фигуры из ответа А позволяют закончить построение квадрата.

Задание 17
|
У Лизы имеется 6 одинаковых треугольников вида
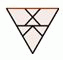
Какую из следующих фигур она может сложить из этих треугольников?
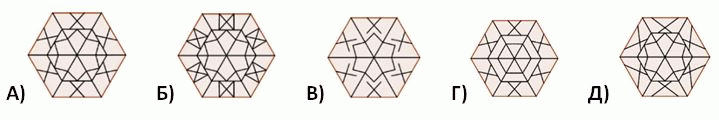
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 62.5 + 5 = 67.5
|
Сравним только одну (верхнюю треугольную) часть шестиугольников в вариантах ответа с тем треугольником, который указан в условии задачи. Видим, что только треугольная часть шестиугольника А совпадает с треугольником из условия задачи. Поэтому правильным является ответ А.
Задание 18
|
Эмма заняла третье место в конкурсе сольных танцев. Между ней и тем, кто занял последнее место, оказалось 3 танцора. Сколько всего танцоров приняло участие в конкурсе?
A) 4 Б) 5 В) 6 Г) 7 Д) 1
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 67.5 - 1.25 = 66.25
|
Так как Эмма заняла 3 место, то у неё выиграли 2 участницы. Согласно условию,
3 + 1 = 4 участницы Эмме проиграли. Поэтому всего в конкурсе участвовало
1 + 2 + 4 = 7 танцоров.
Задание 19
|
У пятерых детей разные возрасты, но один и тот же день рождения. Каждому приготовили торт с числом, указывающим возраст. Лена на два года старше Васи, но на год моложе Алины. Виктор ̶ самый младший. Какой торт у Вари?
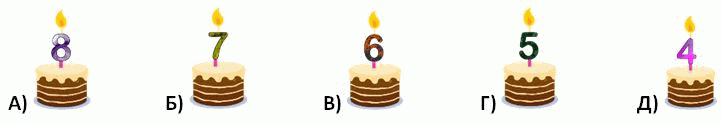
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 66.25 + 5 = 71.25
|
По условию, возрасты детей – 8, 7, 6, 5 и 4 года. Так как Виктор младший, ему 4 года. Далее, Лена на 2 года старше Васи, но на 1 год моложе Алины. Поэтому Алина старше Васи на 2 + 1 = 3 года. Но Васе не менее 5 лет. Тогда Алине не менее 8 лет. Но более быть и не может. Следовательно, Алине 8 лет, Васе 5 лет, а тогда Лене 5 + 2 = 7 лет. Остаётся: Варе 6 лет. Таким образом, правильным является ответ В.
Задание 20
|
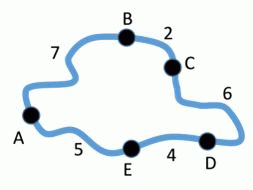
На карте показаны пять деревень A, B, C, D, E, и расстояния в километрах между соседними. Только две деревни находятся на одинаковом расстоянии друг от друга независимо от того, по какому из двух возможных маршрутов ехать. Какие это деревни?
A) B и E
Б) B и D
В) C и E
Г) A и C
Д) A и D
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 71.25 - 1.25 = 70
|
Длина всего кругового пути между указанными деревнями равна
7 + 2 + 6 + 4 + 5 = 24 км.
Поэтому, если между какими-то двумя деревнями два из возможных путей имеют одинаковую длину, то эта длина равна
24 : 2 = 12 км.
На рисунке видно, что это не две соседние деревни. Заметим также, что кратчайшие из двух возможных путей между любыми двумя деревнями не более 12 км. Кратчайшее расстояние от А до С равно
7 + 2 = 9 км,
а до D также равно 5 + 4 = 9 км.
Видим, что ответы Г) и Д), в которых указана деревня А, не являются верными. В трёх парах из оставшихся трёх деревень дважды встречается деревня В. Расстояние между В и Е по обоим путям равно
7 + 5 = 2 + 6 + 4 = 12 км.
Поэтому ответ А) – это один из ответов, который может быть правильным. Он исключает ответ Б). Что касается ответа В), то кратчайшее расстояние от С до Е равно
6 + 4 = 10 км. Видим, что единственным правильным является ответ А) B и Е.
Задание 21
|
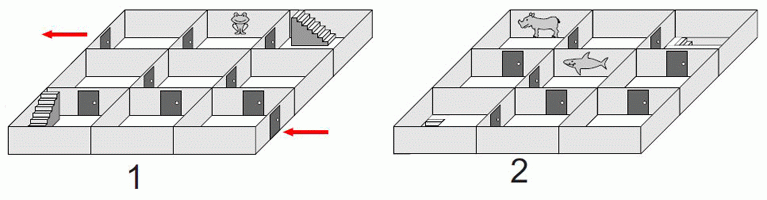
Сеня идёт по двухэтажному лабиринту от входа до выхода, оба расположены на этаже 1. В каком порядке он будет проходить рисунки, изображённые на некоторых стенах?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 70 + 5 = 75
|
Так как Сеня выходит из лабиринта по стрелке на первом этаже, то последним изображением будет рисунок лягушки (см. рис. в условии задачи). Обходных путей для этого не существует. Войдя в лабиринт, он должен подняться на второй этаж по левой ближней лестнице. Далее, закончить свой путь Сеня может, только спустившись со второго этажа по лестнице в правом дальнем углу. Спуститься по этой лестнице непосредственно перед этим он может, только пройдя возле рисунка носорога. Этот рисунок будет предпоследним. Тогда первым будет рисунок акулы. Поэтому правильным
является ответ Б).
Задание 22
|
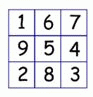
Имеется клетчатая таблица с числами. Амалия хочет наложить на неё одну из следующих 5-клеточных фигур так, чтобы сумма накрытых чисел оказалась наибольшей. Какую из фигур ей следует выбрать? (Фигуры нельзя поворачивать и переворачивать.)

|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 75 - 1.25 = 73.75
|
Все фигуры в вариантах ответа состоят из 5 клеток. Отметим в данном квадрате 5 клеток с наибольшими числами: 9, 8, 7, 6 и 5 (см. рис.).

Видим, что эти клетки образуют фигуру в ответе Д), который и является правильным.
Задание 23
|
В пруду живут три лягушки. Каждую ночь одна из лягушек поёт песню двум другим лягушкам. За 9 ночей одна из лягушек пропела 2 раза. Другая лягушка прослушала 5 песен. Сколько песен прослушала третья лягушка?
A) 7 Б) 6 В) 5 Г) 4 Д) 3
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 73.75 - 1.25 = 72.5
|
По условию, одна из лягушек пела 2 раза. Вторая за 9 ночей прослушала 5 песен. Значит, вторая лягушка пела
9 – 5 = 4 ночи.
Поэтому данные две лягушки пели
2 + 4 = 6 ночей.
Тогда третья лягушка пела
9 – 6 = 3 ночи.
Следовательно, она прослушала
9 – 3 = 6 песен.
Задание 24
|
На четырёх различных карточках напечатаны цифры 1, 1, 2 и 3. Три карточки положили так, чтобы получилось упражнение на вычитание однозначного числа из двухзначного.
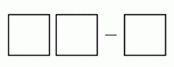
Сколько разных результатов можно получить, если выполнить упражнение?
A) 6 Б) 8 В) 10 Г) 12 Д) 24
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 72.5 + 5 = 77.5
|
Используя цифры 1, 1, 2 и 3 и следуя условию задачи, можно составить 12 разностей:
11 – 3 = 8;
11 – 2 = 9;
12 – 3 = 9;
12 – 1 = 11;
13 – 2 = 11;
13 – 1 = 12;
21 – 3 = 18;
21 – 1 = 20;
23 – 1 = 22;
31 – 2 = 29;
31 – 1 = 30;
32 – 1 = 31.
Но среди них два значения (9 и 11) повторяются дважды. Поэтому различных значений только
12 – 2 = 10.
Таким образом, правильным является ответ В).