Задание 1
|
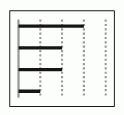
Диаграмма показывает, сколько времени на прошлой неделе Генрих пользовался приложениями, установленными на его смартфоне. На этой неделе на два приложения он потратил столько же времени, а на два другие – в два раза меньше. Как НЕ МОЖЕТ выглядеть соответствующая диаграмма?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Показания на диаграмме в условии задачи можно представить как {3; 2; 2; 1}. Показания в вариантах ответа:
А) {3; 1; 1; 1},
Б) {2; 2; 1,5; 0,5},
В) {2; 1,5; 1; 1},
Г) {3; 2; 1; 0,5},
Д) {3; 2; 2; 0,5}.
Здесь подчёркнуты уменьшенные в 2 раза значения, остальные – равны каким-то исходным. Видим, что в ответе Д уменьшилось не два, а только одно число. Поэтому правильным является ответ Д.
Задание 2
|
Сколько трёхзначных натуральных чисел делятся на 13?
A) 68 Б) 69 В) 70 Г) 76 Д) 77
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Данные числа образуют арифметическую прогрессию с разностью d = 13. Наименьшим трёхзначным числом является число 100. Но 100 = 13 · 7 + 9 на 13 не делится. Тогда первый член этой прогрессии a1 = 13 · 8 = 104. По формуле общего члена арифметической прогрессии, an = 104 + 13(n – 1). Тогда искомое количество чисел – это наибольшее натуральное значение n, для которого выполняется неравенство an < 1000, т.е.
104 + 13(n – 1) < 1000,
или 13n < 909, откуда n < 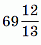 . Поэтому правильным является ответ 69.
. Поэтому правильным является ответ 69.
Задание 3
|
Белла старше Чарли, но моложе Лили. Тедди старше Беллы. У кого из них может быть одинаковый возраст?
A) у Чарли и Тедди
Б) у Тедди и Лили
В) у Лили и Чарли
Г) у Беллы и Лили
Д) у Тедди и Беллы
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 32.25 + 3 = 35.25
|
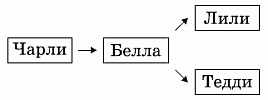
Построим схему, на которой укажем стрелками, кто, в соответствии с условием задачи, старше. Видим, что одного возраста могут быть только Тедди и Лили.
Задание 4
|
Произведение цифр 10-значного числа равно 15. Чему равна сумма цифр этого числа?
A) 8 Б) 12 В) 15 Г) 16 Д) 20
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Так как 15 есть произведение простых чисел 3 и 5, то в записи данного числа должна быть одна цифра 3 и одна цифра 5. Поскольку это число 10-значное, то ещё оно должно иметь восемь цифр 1. Сумма цифр такого числа равна 3 + 5 + 8 · 1 = 16.
Задание 5
|
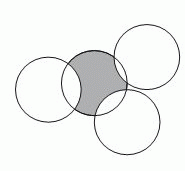
Четыре круга радиуса 1 пересекаются, как показано на рисунке. Чему равен периметр окрашенной фигуры?
A) π
Б) числу между π и 1,5π
В) 1,5π
Г) 2π
Д) π2
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
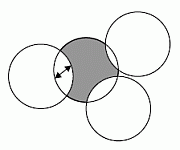
Дуги пересекающихся окружностей одинакового радиуса, заключённые внутри этих окружностей, имеют одинаковую длину (см. рис.). Поэтому периметр окрашенной фигуры равен длине одной такой окружности, т.е. равен 2π.
|
Задание 6
|
Давид выписывает в порядке возрастания все числа от 2 до 2022, в записи которых нет других цифр, кроме 0 и 2. Какое число окажется ровно посередине в таком списке?
A) 200 Б) 220 В) 222 Г) 2000 Д) 2022
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Выпишем в порядке возрастания числа, о которых идёт речь:
2, 20, 22, 200, 202, 220, 222, 2000, 2002, 2020, 2022.
Всего их одиннадцать, и средним является число 220.
Задание 7
|
Сколько действительных корней имеет уравнение
(x − 2)2 + (x + 2)2 = 0?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 41.25 + 3 = 44.25
|
Каждое слагаемое в уравнении неотрицательно и, значит, должно быть равно 0. Поэтому уравнение равносильно системе
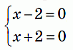 ,
,
которая решений не имеет. Таким образом, число корней данного уравнения равно 0.
Задание 8
|
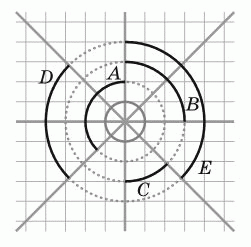
Четыре прямые пересекаются в одной точке и образуют восемь равных углов. Какая из чёрных дуг имеет такую же длину, как серая окружность в центре?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 44.25 - 0.75 = 43.5
|
Примем сторону клетки за 1. Тогда длина окружности в центре равна 2π.
Далее, длины рассматриваемых дуг, учитывая, какую часть окружности они составляют, и учитывая радиусы соответствующих окружностей, равны:
А) 2π · 2 · 3/8 = 3π/2
Б) 2π · 3 · 1/4 = 3π/2
В) 2π · 3 · 1/8 = 3π/4
Г) 2π · 4 · 1/4 = 2π
Д) 2π · 4 · 3/8 = 3π
Видим, что правильным является ответ Г) D.
Задание 9
|
Пусть a, b и c – ненулевые числа. Известно, что числа −2a4b3c2 и 3a3b5c-4 имеют один и тот же знак. Какое из следующих утверждение верно?
A) ab > 0
Б) b < 0
В) c > 0
Г) bc > 0
Д) a < 0
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 43.5
Поскольку чётные степени ненулевых чисел положительны, совпадение знаков у чисел -2a4b3c2 и 3a3b5c-4 равносильно совпадению знаков у чисел -b и ab. А это возможно только при условии a < 0.
По-другому получить правильный ответ можно так. Заметим, что два ненулевых числа имеют один и тот же знак тогда и только тогда, когда их произведение положительно. Поэтому условие задачи равносильно неравенству: –2a4b3c2 · 3a3b5c-4 > 0, или -6a7b8c-2 > 0, откуда a < 0.
|
Задание 10
|

Миша отметил четыре точки на прямой так, как показано на рисунке. Известно, что AC = 12 cм, BD = 18 cм. Каково расстояние между серединами отрезков AB и CD?
A) 15 см Б) 12 см В) 18 см Г) 6 см Д) 9 см
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Пусть BC = x см. Тогда, согласно условию, AC = 12 – x см и CD = 18 – x см. В результате, расстояние между серединами отрезков AB и CD равно
(12-х)/2 + х + (18-х)/2 = 6 + 9 = 15 см.

Задание 11
|
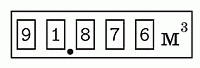
Толя заметил, что на счётчике воды в его квартире все цифры различные (см. рис.). Сколько воды должно быть использовано до ближайшего момента, когда снова на счётчике все цифры будут различными?
A) 0,006 м3 Б) 0,034 м3 В) 0,086 м3 Г) 0,137 м3 Д) 1,048 м3
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 46.5 + 4 = 50.5
|
Увеличение только последних трёх цифр (как по отдельности, так и в совокупности) приводит к числу с совпадающими цифрами. Поэтому, чтобы получить число с различными цифрами, необходимо изменить вторую слева цифру 1. Наименьшее число с различными цифрами, которое больше данного числа на счётчике, – это число 92,013. Оно появится на счётчике после того, как будет израсходовано
92,013 – 91,876 = 0,137 м3 воды.
Задание 12
|
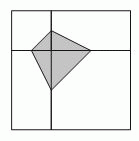
Квадрат разбили на два меньших неравных квадрата и два прямоугольника, как показано на рисунке. Вершины окрашенного четырёхугольника являются серединами соответствующих сторон полученных квадратов. Площадь этого четырёхугольника равна 3. Чему равна площадь неокрашенной части исходного квадрата?
A) 12 Б) 15 В) 18 Г) 21 Д) 24
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 50.5
Пусть сторона исходного квадрата равна а. Заметим, что сумма длины стороны одного из полученных при разбиении квадратов и стороны другого квадрата равна стороне исходного квадрата, т.е. равна а. Тогда длины диагоналей окрашенного четырёхугольника равны половине суммы длин сторон полученных квадратов, т.е. равны a/2. Так как эти диагонали перпендикулярны, площадь окрашенного четырёхугольника можно вычислить по формуле
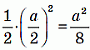
Согласно условию, a2/8 = 3, откуда площадь исходного квадрата a2 = 24. Тогда площадь неокрашенной части квадрата равна 24 – 3 = 21.
По-другому получить правильный ответ можно так. Проведём через вершины окрашенного четырёхугольника отрезки, параллельные сторонам исходного квадрата, как показано на рисунке.
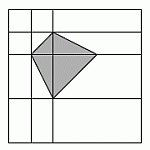
В результате, каждый из меньших квадратов и каждый из двух полученных прямоугольников разбивается на 4 равные части. Только половина от каждой из группы таких частей принадлежит окрашенному четырёхугольнику. Поэтому площадь этого четырёхугольника составляет 1/2 · 1/4 = 1/8 от площади данного квадрата, а неокрашенная часть – 7/8, т.е. в 7 раз больше. Следовательно, площадь неокрашенной части исходного квадрата равна 7 · 3 = 21.
|
Задание 13
|
Чему равен наибольший общий делитель чисел 22021 + 22022 и 32021 + 32022?
A) 22021 Б) 1 В) 2 Г) 6 Д) 12
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 50.5 - 1 = 49.5
|
Имеем:
22021 + 22022 = 22021 · 3
и
32021 + 32022 = 32021 · 4
Поэтому наибольший общий делитель данных двух чисел равен 3 · 4 = 12.
Задание 14
|
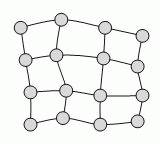
16 городов соединены дорогами так, как показано на рисунке. Правительство хочет построить электростанции в некоторых из этих городов. Каждая электростанция должна обеспечить электроэнергией город, в котором она расположена, и другие города, связанные с данным городом одной дорогой. Какое наименьшее количество электростанций нужно построить, чтобы все города были обеспечены электроэнергией?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 49.5 - 1 = 48.5
|
Каждый из данных городов соединён дорогами не более чем с 4 другими городами. Поэтому если построить не более трёх электростанций, то энергией
будут обеспечены не более 3 + 3 · 4 = 15 городов, что недостаточно. Поэтому понадобится не менее 4 электростанций.
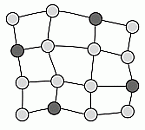
С другой стороны, если 4 электростанции построить в городах, обозначенных на следующем рисунке чёрным цветом, то все условия задачи будут выполнены.
Задание 15
|
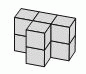
Из каких двух фигур в вариантах ответа можно сложить фигуру на рисунке сверху?

|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 48.5
Рассмотрим фигуры в варианте ответа А). Они одинаковы. Возьмём одну из них и повернём в горизонтальной плоскости (вокруг вертикали) так, как показано на рисунке. Затем повернём её в вертикальной плоскости (вокруг горизонтали).
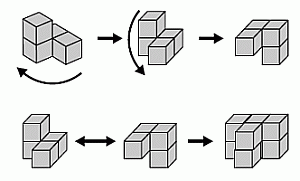
Теперь, если сложить две данные фигуры в двух полученных ракурсах так, как показано на втором рисунке, то видно, что получится фигура, указанная в условии задачи. Следовательно, правильным является ответ А.
Хотя правильный ответ уже найден, можно убедиться, что из фигур в других вариантах ответа нельзя сложить фигуру, указанную в условии задачи.
|
Задание 16
|
В турнире участвуют 8 игроков. Марта знает, что победит всех, кроме Эллы, которая самая сильная и победит всех. В первом туре игроки случайным образом разбиваются на четыре пары. Победитель каждого матча проходит во второй тур, в котором снова пары формируются случайным образом. Победители второго тура выходят в финал. Какова вероятность того, что Марта не пройдёт в финал?
A) 1 Б) 1/2 В) 2/7 Г) 3/7 Д) 4/7
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 48.5 + 4 = 52.5
|
Марта не пройдёт в финал, если она встретится в матче с Эллой в первом туре, либо если она встретится с ней во втором туре. Эти события несовместные. Поэтому искомая вероятность равна сумме вероятностей встречи Марты с Эллой в первом туре и встречи Марты с Эллой во втором туре. В первом туре Марта может встретиться с любой из других 7 соперниц. Элла – одна из них. Поэтому вероятность встречи с Эллой равна 1/7. Вероятность пройти Марты во второй тур равна 1 – 1/7 = 6/7. При этом Элла во втором туре будет одной из трёх её соперниц. Поэтому вероятность встречи Марты с Эллой во втором туре равна (6/7) · (1/3) = 2/7. В результате, вероятность того, что Марта не пройдёт в финал, равна 1/7 + 2/7 = 3/7.
Задание 17
|
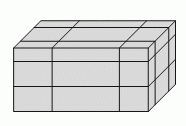
Прямоугольный параллелепипед плоскостями, параллельными граням, разбит на 27 меньших параллелепипедов, как показано на рисунке. Площадь поверхности данного параллелепипеда равна S. Чему равна сумма поверхностей всех 27 полученных параллелепипедов?
A) 2S Б) 2,5S В) 3S Г) 4S Д) другой ответ
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 52.5
Пусть площади различных граней данного параллелепипеда равны a, b и c. Тогда
S = 2(a + b + c).
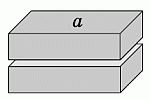
Заметим, что один разрез параллелепипеда, параллельный грани площадью а, увеличивает общую поверхность получаемых частей на 2a (см. рис.), соответственно, два разреза – на 4a. Аналогичные изменения происходят и при разрезах, параллельных другим граням. Поэтому после всех указанных разрезов общая поверхность всех полученных частей будет равна
6(a + b + c) = 3S.
|
Задание 18
|
Среднее арифметическое пяти чисел равно 24. Среднее арифметическое трёх наименьших из них равно 19, а трёх наибольших – 28. Чему равно среднее по величине число?
A) 20 Б) 21 В) 22 Г) 23 Д) 24
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 52.5 + 4 = 56.5
|
Из условия задачи следует, что сумма данных пяти чисел равна 24 · 5 = 120, сумма трёх наименьших из них равна 19 · 3 = 57, а сумма трёх наибольших равна 28 · 3 = 84. Среднее по величине число входит как слагаемое и в меньшую тройку, и в большую. Поэтому, если сложить сумму трёх наименьших чисел и сумму трёх наибольших, то мы получим сумму всех пяти чисел плюс среднее число. Следовательно, это число равно
57 + 84 – 120 = 21.
Задание 19
|
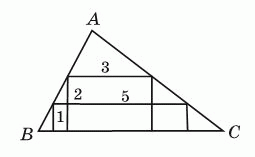
Два прямоугольника 1 × 5 и 2 × 3 вписаны в треугольник ABC так, как показано на рисунке. Чему равна высота данного треугольника, опущенная на сторону BC?
A) 3
Б) 3,5
В) 8/3
Г) 16/5
Д) другой ответ
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 56.5
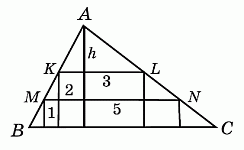
Пусть h – искомая высота треугольника
ABC (см. рис.). Из условия задачи следует, что треугольники AKL и AMN подобны. Вследствие их подобия имеем (h - 2)/3 = (h - 1)/5, откуда 5(h – 2) = 3(h – 1), или 5h – 10 = 3h – 3, или 2h = 7, т.е. h = 3,5.
|
Задание 20
|
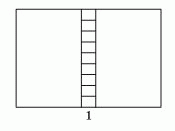
Прямоугольник на рисунке разбит на 11 меньших прямоугольников, подобных исходному. Ориентация самых маленьких прямоугольников такая же как у исходного прямоугольника. Большая сторона одного из самых маленьких прямоугольников равна 1. Чему равен периметр исходного прямоугольника?
A) 20 Б) 24 В) 27 Г) 30 Д) 36
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 56.5
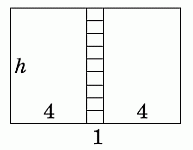
На рисунке в условии задачи видно, что по высоте исходного прямоугольника помещается 9 прямоугольников с основанием 1. Они подобны исходному прямоугольнику (с той же ориентацией). Поэтому основание исходного прямоугольника равно 9, и тогда основания левого и правого больших прямоугольников равны (9 - 1)/2 = 4.
Пусть высота исходного прямоугольника (а значит, и высота двух боковых прямоугольников) равна h. Из подобия получаем пропорцию 9/h = h/4, откуда h2 = 36 и, значит, h = 6. В результате, периметр исходного прямоугольника равен 2(9 + 6) = 30.
|
Задание 21
|
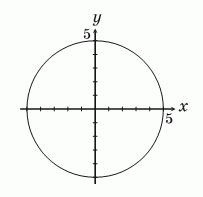
Окружность с центром в начале координат имеет радиус 5. Сколько всего на этой окружности точек, у которых обе координаты являются целыми числами?
A) 5 Б) 8 В) 12 Г) 16 Д) 20
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 56.5 + 5 = 61.5
|
Данная окружность имеет уравнение x2 + y2 = 52.
Все возможные значения переменных, удовлетворяющие условию задачи, находятся в пределах от –5 до 5. Рассмотрим все целые значения x в этих пределах.
При x = 0 получаем два значения y = ±5. Это даёт две точки с целыми координатами: (0; ±5).
При x = ±1 получаем
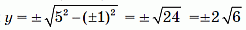 – не целые значения.
– не целые значения.
При x = ±2 получаем
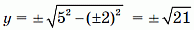 – также не целые значения.
– также не целые значения.
При x = ±3 получаем
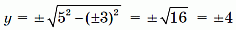 – целые значения. Это даёт четыре целые точки: (±3; ±4) (с любыми комбинациями знаков).
– целые значения. Это даёт четыре целые точки: (±3; ±4) (с любыми комбинациями знаков).
При x = ±4 получаем
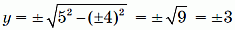 – целые значения. Это даёт ещё четыре целые точки: (±4; ±3).
– целые значения. Это даёт ещё четыре целые точки: (±4; ±3).
Наконец, при x = ±5 получаем
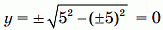 – целое значение. Это даёт две целые точки: (±5; 0).
– целое значение. Это даёт две целые точки: (±5; 0).
Таким образом, всего на данной окружности находится 2 + 4 + 4 + 2 = 12 точек с целыми координатами.
Задание 22
|
Сколько существует трёхзначных натуральных чисел, которые в 5 раз больше произведения их цифр?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 61.5
Пусть искомое число равно 100a + 10b + c (a, b, c – его цифры). Тогда, согласно условию,
100a + 10b + c = 5abc.
Из полученного равенства следует, что с делится на 5. При этом с ≠ 0, иначе правая часть уравнения равна 0, а значит, искомое число тоже 0, противоречие. Следовательно, с = 5. Тогда, сократив на 5, получим:
20a + 2b + 1 = 5ab.
Левая часть последнего неравенства – нечётное число. Значит, и правая часть – нечётное число. Поэтому обе цифры a и b тоже нечётные. Кроме того, из равенства следует, что 2b + 1 делится на 5. Тогда единственное возможное значение b = 7. Подставив его в уравнение выше, получим 20a + 15 = 35a, откуда a = 1. Таким образом, только число 175 удовлетворяет условию задачи. Тем самым, правильным является ответ 1.
|
Задание 23
|
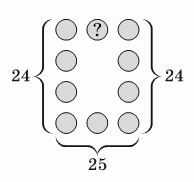
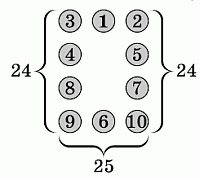
В кружочки на рисунке вписаны числа от 1 до 10 (каждое ровно один раз). Суммы чисел в левом и в правом столбцах равны 24. Сумма чисел в нижней строке равна 25. Чему равно число в кружочке, отмеченном знаком вопроса?
A) 2
Б) 4
В) 5
Г) 6
Д) ни одно из предыдущих
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 61.5
Согласно условию задачи, сумма чисел в столбцах и нижней строчке равна 24 + 24 + 25 = 73. В эту сумму входят все данные числа, кроме искомого числа. При этом два числа (нижние в столбцах) входят в эту сумму дважды. Оценим наибольшее возможное значение такой суммы. Оно равно
10 + 10 + 9 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 = 73.
Следовательно, условия задачи могут быть выполнены, только если искомым является число 1. Тем самым, правильным является ответ Д.
Хотя это не обязательно для решения, приведём пример, показывающий, что описанная в условии ситуация возможна (см. рис.).
|
Задание 24
|
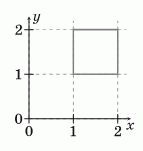
Квадрат со стороной 1 расположен на координатной плоскости так, как показано на рисунке. Каждую его точку (x, y) заменили на точку 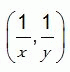 .
.
Какая фигура в результате получилась?

|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 61.5 - 1.25 = 60.25
|
Вершины данного квадрата переходят в вершины квадрата со стороной 0,5:
(1; 1) → (1; 1), (1; 2) → (1; 0,5), (2; 2) → (0,5; 0,5), (2; 1) → (0,5; 1).
Видим, что ответы Б, Г и Д не являются верными.
Далее, на каждой из сторон данного квадрата одна из координат точек принимает фиксированное значение. Поэтому и у полученного образа имеет место такое же свойство, т.е. граница образа состоит из вертикальных и горизонтальных отрезков. Следовательно, образ – это квадрат и, значит, правильным является ответ В.
Задание 25
|
Вершины 20-угольника пронумерованы числами от 1 до 20 так, что номера соседних вершин отличаются только на 1 или на 2. Стороны, вершины на концах которых отличаются на 1, окрасили в красный цвет. Сколько красных сторон могло получиться?
A) 1
Б) 2
В) 5
Г) 10
Д) имеется несколько различных возможностей
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 60.25
Заметим, что числа 1 и 20 (разность между ними наибольшая) должны находиться в противоположных вершинах. Действительно, предположим, что это не так. Тогда из двух путей, которые состоят из сторон данного 20-угольника и ведут от вершины с номером 1 до вершины с номером 20, один будет состоять не более чем из 9 отрезков. Однако переход по отрезку от одной вершины к соседней, по условию, увеличивает номер вершины не более чем на 2. Поэтому на концах такого пути не могут стоять числа, разница между которыми больше 9 · 2 = 18.
Итак, числа 1 и 20 должны быть номерами противоположных вершин. При этом, чтобы условия задачи были
выполнены, на каждом из двух путей, ведущем от числа 1 к числу 20, должно быть 9 отрезков, на которых номер увеличивается на 2, и 1 отрезок, на котором номер увеличивается на 1. Такая нумерация возможна. Для этого на одном
из рассматриваемых путей должны быть все чётные номера, а на другом – все нечётные (см. рис.). Таким образом,
могло быть только 2 красные стороны.
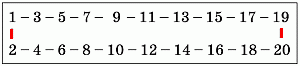
|
Задание 26
|
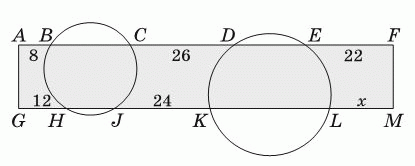
Две окружности пересекают прямоугольник AFMG так, как показано на рисунке. Известно, что AB = 8, CD = 26, EF = 22, GH = 12 и JK = 24. Какую длину имеет отрезок LM?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 60.25 + 5 = 65.25
|
Решим задачу в общем виде. Пусть отрезки, длины которых указаны в условии задачи, и отрезок, который нужно найти, – это a, b, c, d, e и f.
Докажем, что справедливо равенство:
a + e + c = d + b + f. (*)
Для этого проведём серединный перпендикуляр к хорде BС. Он пройдёт через центр окружности и будет также перпендикуляром к хорде HJ, а значит, будет серединным перпендикуляром и для этой хорды. Такой же перпендикуляр проведём и для хорд другой окружности. Обозначим половины хорд так, как показано на рисунке.
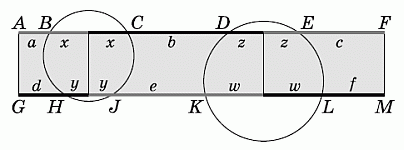
Построенные перпендикуляры разбивают данный прямоугольник на три меньших прямоугольника. А поскольку противоположные стороны прямоугольника равны, справедливы равенства:
a + x = d + y,
y + e + w = x + b + z,
z + c = w + f.
Сложив эти три равенства, получим:
a + x + y + e + w + z + c = d + y + x + b + z + w + f.
Удалив слева и справа одинаковые слагаемые, получаем равенство (*). При числовых данных в условии задачи,
согласно доказанному равенству, имеем: 8 + 24 + 22 = 12 + 26 + x, откуда x = 16.
Задание 27
|
Пусть N – натуральное число. Сколько натуральных чисел на числовой прямой находится между числами
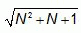 и
и 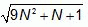 ?
?
A) N + 1
Б) 2N – 1
В) 2N
Г) 2N + 1
Д) 3N
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 65.25
Заметим, что
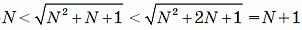
и
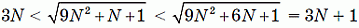
Поэтому натуральными на указанном промежутке являются числа от N + 1 до 3N включительно. Количество таких чисел равно 2N.
|
Задание 28
|
В последовательности an: 0 < a1 < 1 и a2n = a2an + 1, a2n + 1 = a2an – 2 для всех n ≥ 1. Известно, что a7 = 2. Чему равно значение a2?
A) a1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 65.25 - 1.25 = 64
|
Будем вести расчёты с конца, начав с a7 = 2. Из условия задачи следует, что
a2n – a2n + 1 = 3.
Тогда a6 = a7 + 3 = 2 + 3 = 5.
Далее, так как
a6 = a2a3 + 1, то
a2a3 = 5 – 1 = 4. Кроме того,
a2 – a3 = (a2a1 + 1) – (a2a1 – 1) = 3,
откуда a3 = a2 – 3. Тогда получаем уравнение
a2 (a2 – 3) = 4,
или a22 – 3a2 – 4 = 0. Оно имеет два корня: 4 и –1.
Но если a2 = –1, то из a2 = a2a1 + 1 получим -1 = -a1 + 1, откуда a1 = 2. Получаем противоречие с условием 0 < a1 < 1.
Если же a2 = 4, то аналогично из равенства a2 = a2a1 + 1 находим a1 = 3/4. Тем самым, все условия выполнены и,
значит, правильным является ответ 4.
Задание 29
|
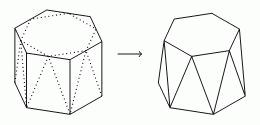
Верхние углы правильной шестиугольной призмы срезали, как показано на рисунке. Верхняя грань стала меньшим правильным шестиугольником, а 6 боковых прямоугольных граней преобразовались в 12 равнобедренных треугольников двух разных размеров. На какую часть уменьшился объём призмы?
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 64
Пусть сторона шестиугольника в основании данной призмы равна а, а высота призмы равна h. Правильный шестиугольник со стороной а состоит из 6 равносторонних треугольников со стороной а. Площадь одного такого треугольника равна 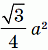 .
.
Тогда площадь основания данной призмы равна 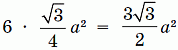 ,
,
а объём 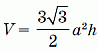 .
.
Теперь найдём объём вырезанных частей. Они представляют собой 6 одинаковых пирамид высотой h. Основаниями таких пирамид являются равнобедренные треугольники с боковыми сторонами a/2 и углом 120° между ними (эти углы – углы шестиугольника в основании призмы; см. рис.).
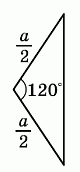
Площадь такого треугольника равна  .
.
Тогда объём одной вырезанной пирамиды равен 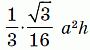 ,
,
а объём всех шести вырезанных частей равен 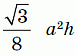 .
.
Это составляет 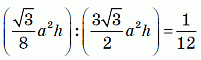 часть от объёма призмы.
часть от объёма призмы.
По-другому решить задачу можно так. Разобьём правильный шестиугольник в основании данной призмы на равнобедренные треугольники так, как показано на следующем рисунке.
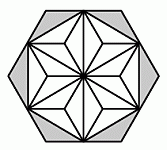
Всего таких треугольников 24, все они одинаковые и имеют такие размеры, как на верхнем рисунке. Шесть окрашенных треугольников оказались вырезаны из верхней грани, что составляет 6/24 = 1/4 часть от её площади. Поскольку были вырезаны пирамиды, а объём пирамиды в 3 раза меньше объёма призмы с тем же основанием и той же высотой, то объём вырезанных частей составляет 1/3 · 1/4 = 1/12 часть объёма данной призмы.
|
Задание 30
|
Футбольный матч между командами Северного Берракана и Южного Берракана проходит на стадионе с прямоугольной трибуной для зрителей. В каждом ряду кресел сидят 11 фанатов Северного Берракана, а в каждом столбце трибуны – 14 фанатов Южного Берракана. 17 мест оказались пустыми. Какое наименьшее количество мест может быть на зрительской площадке стадиона?
A) 500 Б) 660 В) 690 Г) 840 Д) 994
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 64 - 1.25 = 62.75
|
Пусть на зрительской площадке стадиона r рядов и в каждом ряду m мест. Тогда всего на стадионе rm мест.
С другой стороны, согласно условию, на стадионе 11r + 14m + 17 мест. Получаем уравнение:
rm = 11r + 14m + 17 ⇔
⇔ rm – 11r – 14m + 14 · 11 = 14 · 11 + 17 ⇔
⇔ r(m – 11) – 14(m – 11) = 171 ⇔
⇔ (r – 14)(m – 11) = 32 · 19.
Тогда пара (r – 14; m – 11) может принимать следующие значения:
(1; 171), (3; 57), (9; 19), (19; 9), (57; 3), (171; 1).
Вследствие этого пара (r; m) может принимать соответственно следующие значения
(15; 182), (17; 68), (23; 30), (33; 20), (71; 14), (185; 12).
В результате, число мест на стадионе, равное rm, может принимать значения 15 · 182 = 2730, 17 · 68 = 1156, 23 · 30 = 690, 33 · 20 = 660, 71 · 14 = 994, 185 · 12 = 2220.
Видим, что наименьшее возможное количество мест на стадионе равно 660.





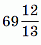 . Поэтому правильным является ответ 69.
. Поэтому правильным является ответ 69.


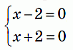 ,
,




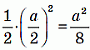













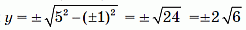 – не целые значения.
– не целые значения.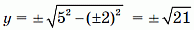 – также не целые значения.
– также не целые значения.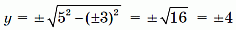 – целые значения. Это даёт четыре целые точки: (±3; ±4) (с любыми комбинациями знаков).
– целые значения. Это даёт четыре целые точки: (±3; ±4) (с любыми комбинациями знаков).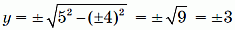 – целые значения. Это даёт ещё четыре целые точки: (±4; ±3).
– целые значения. Это даёт ещё четыре целые точки: (±4; ±3).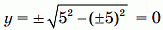 – целое значение. Это даёт две целые точки: (±5; 0).
– целое значение. Это даёт две целые точки: (±5; 0).


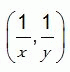 .
.
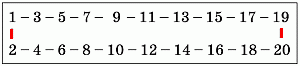


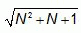 и
и 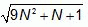 ?
?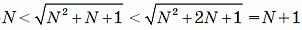
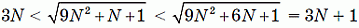

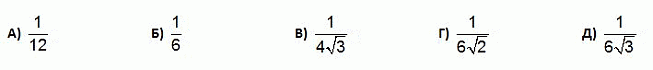
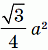 .
.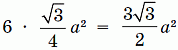 ,
,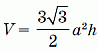 .
.
 .
.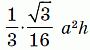 ,
,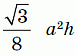 .
.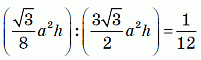 часть от объёма призмы.
часть от объёма призмы.
