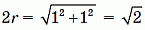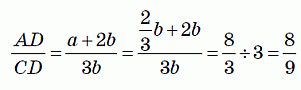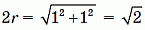Задание 1
|
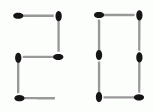
Кирилл складывает число 2022 из спичек в коробке. Вначале в коробке было 30 спичек. Кирилл сложил первые две цифры так, как показано на рисунке. Сколько спичек останется в коробке после того, как он сложит все четыре цифры?
A) 20 Б) 192 В) 10 Г) 9 Д) 5
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 30 + 3 = 33
|
На рисунке в условии задачи видно, что цифра 2 состоит из пяти спичек,
а цифра 0 – из шести спичек. Поэтому, чтобы сложить число 2022, нужно использовать 3 · 5 + 6 = 21 спичку. После этого в коробке останется 30 – 21 = 9 спичек.
Задание 2
|
Квадрат и равносторонний треугольник имеют одинаковые периметры. Сторона треугольника равна 12. Чему равна сторона квадрата?
A) 9 Б) 12 В) 16 Г) 24 Д) 36
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Периметр треугольника со стороной 12 равен 12 · 3 = 36. Сторона квадрата, имеющего такой же периметр, равна 36 : 4 = 9.
Задание 3
|
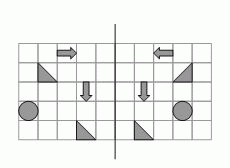
На листе бумаги нарисованы некоторые фигуры (см. рис.). Учитель согнул лист так, что левая половина листа совместилась с правой. Сколько фигур на левой части листа в точности совместились с фигурами на правой части листа?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
После сгибания листа совместятся ровно 3 фигуры: в первой, второй и третьей строчках (см. рисунок). Кружочки в четвёртой строчке не совместятся вследствие разного расстояния до
линии сгиба. Треугольники в пятой строчке не совместятся вследствие их несимметричности.
Задание 4
|
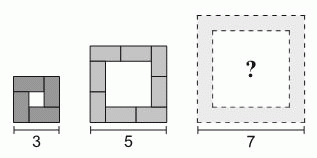
Катя складывает квадратные фигуры из доминошек 2 × 1 так, как показано на рисунке. Сколько доминошек ей понадобится для третьей фигуры?
A) 10 Б) 11 В) 12 Г) 14 Д) 16
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 31.5 + 3 = 34.5
|

Третья фигура на рисунке справа состоит из 12 доминошек.
Задание 5
|
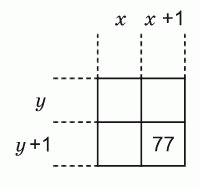
В клетки таблицы вписывают произведения целых чисел, записанных в соответствующих строчках и столбцах. На рисунке указано одно из произведений. Чему равно произведение xy?
A) 72 Б) 70 В) 66 Г) 60 Д) 56
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
Согласно условию, (x + 1)(y + 1) = 77. Учитывая, что множители в скобках больше 1, произведение 77 можно получить (с точностью до порядка следования множителей) только единственным образом: 77 = 7 · 11. Поэтому xy = 6 · 10 = 60.
Задание 6
|
Некоторое число меньше его половины, но больше удвоенного значения. А сумма этого числа и его квадрата равна 0. Какое это число?
A) -2 Б) -1 В) 0 Г) 1 Д) 2
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 33.75 - 0.75 = 33
|
Пусть x – искомое число. Согласно условию,
2x < x < 0,5x и x + x2 = 0.
Второе условие равносильно x(1 + x) = 0, откуда x = 0 или x = –1. Но x = 0 не удовлетворяет первому условию (оно приобретает вид 0 < 0 < 0). А при x = –1 первое условие превращается в правильное двойное неравенство –2 < –1 < –0,5. Поэтому правильным является ответ –1.
Задание 7
|
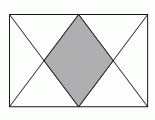
В прямоугольнике середины горизонтальных сторон соединены отрезками с вершинами так, как показано на рисунке. Какую часть от площади данного прямоугольника составляет площадь серого четырёхугольника?
A) 1/5 Б) 1/4 В) 2/7 Г) 1/3 Д) 2/5
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 33 + 3 = 36
|
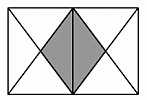
Соединив отрезком середины горизонтальных сторон данного прямоугольника, мы получим его разбиение на 8 треугольников. Легко видеть, что они равновелики. Два из них образуют серый четырёхугольник. Поэтому его площадь составляет 2/8 = 1/4 часть от площади данного прямо угольника.
Задание 8
|
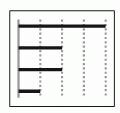
Диаграмма показывает, сколько времени на прошлой неделе Надя пользовалась приложениями, установленными на её смартфоне. На этой неделе на два приложения она потратила столько же времени, а на два другие – в два раза меньше. Как может выглядеть соответствующая диаграмма?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 36 + 3 = 39
|
В ответе А время на все приложения сократилось в 2 раза. В ответе Б время только на третье приложение уменьшилось в 2 раза. Оба эти ответа не являются верными. А в ответе В время ровно на два приложения уменьшилось в 2 раза. Это и есть правильный ответ.
Хотя правильный ответ уже найден, можно убедиться, что диаграммы Г и Д не соответствуют изменениям, указанным в условии задачи.
Задание 9
|
В школьных выборах участвуют 5 кандидатов. После подсчёта 90% голосов результаты оказались следующими: Алексей – 14; Белла – 11; Валя – 10; Галя – 8; Дима – 2. Сколько из кандидатов сохраняют шансы оказаться победителем после подсчёта всех голосов?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Согласно условию задачи, 90% голосов – это
14 + 11 + 10 + 8 + 2 = 45 голосов.
Тогда 10% голосов, которые ещё не подсчитаны, – это
45 · (10% : 90%) = 5 голосов.
Поэтому шансы выиграть выборы сохраняют 3 кандидата с числами голосов 14, 11 и 10. Если любое из этих чисел увеличить на 5, то получим число, большее всех остальных
четырёх чисел, указывающих количество полученных другими кандидатами голосов.
Кандидаты с 8 и 2 голосами не имеют шанса победить. При увеличении их числа голосов на 5 они не выиграют у Алексея с его 14 голосами.
Задание 10
|
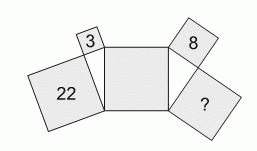
Пять квадратов и два прямоугольных треугольника расположены так, как показано на рисунке. Площади трёх из этих квадратов указаны. Чему равна площадь квадрата, отмеченного знаком вопроса?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Площадь квадрата равна квадрату его стороны. Тогда, согласно теореме Пифагора, квадрат стороны среднего квадрата на рисунке равен 22 + 3 = 25.
Далее, по теореме Пифагора, квадрат стороны квадрата со знаком вопроса равен 25 – 8 = 17. Таким образом, знаком вопроса отмечен квадрат, площадь которого равна 17.
Задание 11
|
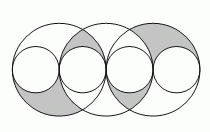
На рисунке показаны три больших окружности одинакового радиуса и четыре меньших окружности радиуса 1. Центры всех окружностей и точки их касания находятся на одной прямой. Чему равна площадь серой фигуры?
A) π Б) 2π В) 3π Г) 4π Д) 6π
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 41.25 - 1 = 40.25
|
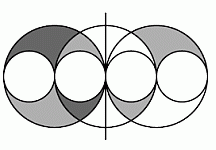
Отразим две серые части, расположенные внутри третьего круга, симметрично относительно вертикальной прямой, проходящей через центр второй большой окружности (см. рис.). Тогда
все серые части данной фигуры образуют первый большой круг, без двух находящихся внутри меньших кругов. Из условия следует, что радиусы больших кругов равны 2. Поэтому площадь одного большого круга равна 4π. Площадь двух маленьких кругов радиуса 1 равна 2π. В результате, площадь серой фигуры равна 4π – 2π = 2π.
Задание 12
|
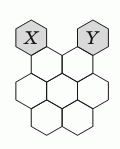
Пчела переползает по сотам через общие стороны ячеек из X в Y. Она хочет по пути побывать ровно один раз в каждой из семи белых ячеек. Сколько различных путей для этого существует?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.25 + 4 = 44.25
|
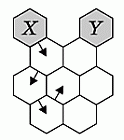
Заметим, что существует ровно 5 способов, как можно войти в центральную белую ячейку. На рисунке показан один из них (здесь вход в центральную соту осуществлён с третьей после X соты). После центральной соты дальнейший путь продолжается однозначно. Поэтому существует ровно 5 путей, удовлетворяющих условию задачи.
Задание 13
|
В семье 6 детей. Их возрасты – 6 последовательных натуральных чисел. Каждому из детей задали вопрос: «Сколько лет самому старшему из твоих пяти братьев и сестёр?» Каким из следующих чисел НЕ МОЖЕТ быть сумма всех шести полученных в ответах чисел?
A) 55 Б) 125 В) 167 Г) 205 Д) 233
Примечание:
Правильными являются два варианта: A и Г
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 44.25 + 4 = 48.25
|
Пусть n – возраст старшего из детей в данной семье. Тогда пять детей на заданный вопрос назовут число n, а самый старший назовёт число (n – 1). В результате сумма шести названных чисел будет равна
(6n – 1). Это значит, что сумма всех названных детьми чисел, увеличенная на 1, делится на 6. Легко убедиться, что числами в вариантах ответа, которое этим свойством не обладают, являются числа 55 и 205.
Задание 14
|
Ева выложила в ряд 2022 карточки. Адам взял каждую шестую из этих карточек. Затем Боря взял каждую пятую из оставшихся карточек, Валя – каждую четвёртую из оставшихся, а Галя – все оставшиеся карточки. Сколько карточек досталось Гале?
A) 0 Б) 337 В) 674 Г) 1011 Д) 1348
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 48.25 - 1 = 47.25
|
После того как Адам взял каждую шестую карточку, осталось пять шестых от того, что было, т.е.
2022 · 5/6 карточек.
Далее, после того как Боря взял каждую пятую карточку, осталось четыре пятых от того, что осталось после Адама, т.е.
2022 · 5/6 · 4/5 карточек.
Аналогично, после того как Валя взяла каждую четвёртую карточку, осталось
2022 · 5/6 · 4/5 · 3/4 = 2022 · 1/2 = 1011 карточек.
Столько карточек досталось Гале.
По-другому правильный ответ можно было найти так. Если разбить все карточки на 6 равных частей (2022 делится на 6), то можно заметить, что Адаму, Боре и Вале досталось по одной такой части. Поэтому Гале достались оставшиеся 3 части из шести, т.е. половина, а именно,
2022 : 2 = 1011 карточек.
Задание 15
|
Трое внуков спросили у бабушки, сколько ей лет. Бабушка сказала: «Угадайте.» Первый из внуков, предположил, что бабушке 75 лет, второй – 78, третий – 81. Оказалось, что кто-то из них ошибся на 1 год, кто-то – на 2 и кто-то – на 4. Сколько лет бабушке?
A) 76
Б) 77
В) 79
Г) 80
Д) невозможно определить однозначно
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 47.25 + 4 = 51.25
|
Бабушке не может быть 76 лет, так как числа 76 и 81 отличаются более чем на 4. А также бабушке не может быть 80 лет, так как числа 80 и 75 отличаются более чем на 4.
Но бабушке может быть 77 лет или 79 лет, так как 77 = 75 + 2 = 78 – 1 = 81 – 4 и 79 = 75 + 4 = 78 + 1 = 81 – 2, т.е. все условия задачи для этих чисел выполняются. Поэтому однозначно определить возраст бабушки невозможно.
Задание 16
|
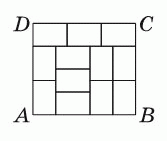
Прямоугольник ABCD на рисунке состоит из 12 меньших одинаковых прямоугольников. Чему равно отношение AD/CD?
A) 8/9 Б) 5/6 В) 7/8 Г) 2/3 Д) 9/8
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 51.25 - 1 = 50.25
|
Пусть прямоугольник ABCD составлен из прямоугольников размера a × b.
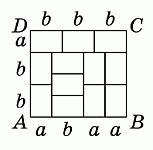
Тогда 3b = b + 3a (см. рис.), откуда a = 2/3 b. Тогда
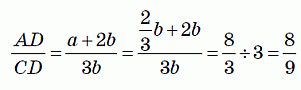
Задание 17
|
Кролик и ёжик соревновались в беге по круговой дорожке длиной 550 м. Они выбежали одновременно с точки старта с постоянными скоростями в противоположных направлениях. Скорость кролика равна 10 м/с, а ёжика – 1 м/с. Когда они встретились, ёжик тут же развернулся и побежал за кроликом. Через какое время после кролика ёжик достиг точки старта?
A) 45 с Б) 50 с В) 55 с Г) 100 с Д) 505 с
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 50.25 - 1 = 49.25
|
Скорость кролика – 10 м/с. Поэтому весь круг (от точки старта до точки старта) длиной 550 м он пробежал за 550 : 10 = 55 с. Двигаясь навстречу, кролик и ёжик сближались со скоростью 10 + 1 = 11 м/с. Поэтому они встретились через 550 : 11 = 50 с. На обратный путь (от точки встречи до точки старта) ёжику понадобилось также 50 с. В результате он прибыл в точку старта через 50 + 50 = 100 с после начала движения. Следовательно, он достиг точки старта через 100 – 55 = 45 с после кролика.
Задание 18
|
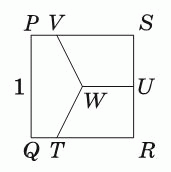
Сторона квадрата PQRS равна 1. Точка U – середина стороны SR, а точка W – центр квадрата. Отрезки TW, VW и UW делят квадрат на три равновеликие части. Чему равна длина VS?
A) 1/2 Б) 2/3 В) 3/4 Г) 4/5 Д) 5/6
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 49.25 - 1 = 48.25
|
Из условия следует, что площадь данного квадрата равна 1 и, значит площадь каждой из трёх частей, на которые он разделён, равна 1/3. Рассмотрим одну из таких частей – трапецию VSUW.
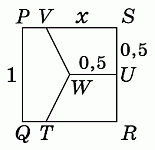
Пусть VS = x. Так как W – центр данного квадрата, WU = 0,5 и SU = 0,5. Тогда, согласно формуле площади трапеции, получаем уравнение:
(x + 0,5)/2 · 0,5 = 1/3,
или x + 0,5 = 4/3 , откуда
x = 4/3 – 1/2 = 5/6.
Задание 19
|
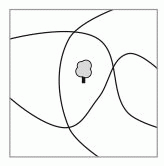
На рисунке показаны три дорожки в парке и одно дерево. Какое наименьшее количество деревьев нужно ещё посадить в парке, чтобы у каждой дорожки по обе стороны было одинаковое число деревьев?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 48.25 - 1 = 47.25
|
Рассмотрим какую-нибудь дорожку. Если в парке по обе стороны от неё деревьев будет поровну, то это значит, что число деревьев в парке будет чётным.
Далее, двух деревьев для выполнения условия задачи для всех трёх дрожек недостаточно. (Действительно, рассмотрим, например, дорожку, соединяющую нижнюю и верхнюю стороны квадратного парка. Если будет посажено ещё только одно дополнительное дерево, то оно должно быть слева по отношению к уже имеющемуся. Слева есть три области, ограниченные дорожками. Рассматривая их по очереди, непосредственно убеждаемся, что ни в одной из них нельзя посадить дерево так, чтобы условие задачи было выполнено для всех трёх дорожек.). Таким образом, в парке должно быть не менее четырёх деревьев, т.е. ещё нужно посадить не менее трёх деревьев.
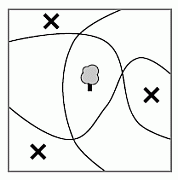
С другой стороны, если 3 дерева посадить в тех частях парка, которые на
рисунке отмечены крестиком, то для
каждой дорожки по обе стороны будет по
2 дерева, тем самым, все условия задачи будут выполнены. Следовательно, правильным является ответ 3.
Задание 20
|
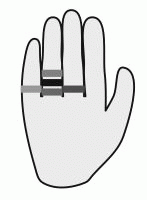
У Вероники 5 колец на пальцах руки расположены так, как показано на рисунке. Она хочет снять их по очереди одно за другим. Сколько существует различных способов это сделать?
A) 16 Б) 20 В) 24 Г) 30 Д) 45
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 47.25 - 1 = 46.25
|
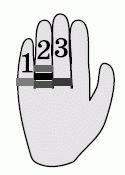
Пронумеруем пальцы, на которых находятся кольца, так, как показано на рисунке. Тогда каждый способ можно представить в виде кода – пятизначного числа, цифры которого указывают номер пальца, с которого на данном шаге снимается кольцо. Такой код имеет по одной цифре 1 и 3 и три цифры 2. Искомое число способов равно количеству таких кодов. Количество перестановок пяти различных элементов равно
5! = 1 · 2 · 3 · 4 · 5 = 120.
Однако в наших кодах имеется 3 одинаковые цифры, перестановки которых не меняют код. Число таких перестановок равно
3! = 1 · 2 · 3 = 6.
Поэтому число различных кодов (и тем самым, число способов снятия колец) равно
(5!) : (3!) = 120 : 6 = 20.
Задание 21
|
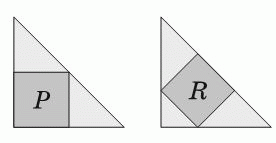
В два одинаковых равнобедренных прямоугольных треугольника вписаны квадраты так, как показано на рисунке. Площадь квадрата P равна 45. Чему равна площадь квадрата R?
A) 35 Б) 40 В) 45 Г) 50 Д) 60
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 46.25 - 1.25 = 45
|
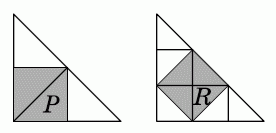
Разобьём данные треугольники на части так, как показано на рисунке. Первый треугольник состоит из четырёх равных частей, две из них образуют квадрат P. Так как площадь этого квадрата равна 45, площадь всего треугольника равна 90. Второй треугольник состоит из девяти равных частей, четыре из них образуют квадрат R. Поэтому, так как площадь всего треугольника равна 90, площадь квадрата R равна 4/9 · 90 = 40.
Задание 22
|
В футбольном турнире участвуют 8 команд. Каждая команда должна сыграть с каждой другой один матч. За выигрыш в матче команда получает 3 очка, за проигрыш – 0 очков, за ничью – 1 очко. После окончания турнира все команды в сумме имели 61 очко. Какое наибольшее число очков могла получить команда-победитель турнира?
A) 21 Б) 19 В) 18 Г) 17 Д) 16
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 45 + 5 = 50
|
Если каждая из 8 команд сыграет с каждой из других 7 команд, то всего будет сыграно 8 · 7 / 2 = 28 матчей (учитывая, что в каждом матче участвует 2 команды).
Минимальное число очков, разыгрываемое в матче, равно 2 (тот случай, когда матч закончился вничью). Если бы все матчи закончились вничью, то в сумме все команды набрали бы 28 · 2 = 56 очков. Но в данном матче команды набрали на 61 – 56 = 5 очков больше. Это значит, что было ровно 5 результативных матчей, когда одна команда победила другую и получила 3 очка. Поэтому наибольшее число очков могла получить команда, которая выиграла все эти 5 матчей и 2 свела вничью. Она получила бы 5 · 3 + 2 · 1 = 17 очков.
Задание 23
|
Пираты поделили между собой 200 золотых и 600 серебряных монет. Каждый офицер получил 5 золотых и 10 серебряных монет. Каждый моряк получил 3 золотых и 8 серебряных монет. Каждый юнга получил 1 золотую и 6 серебряных монет. Сколько всего было пиратов?
A) 50 Б) 60 В) 72 Г) 80 Д) 90
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Заметим, что каждый из пиратов (офицер, моряк, юнга) получил ровно на 5 серебряных монет больше, чем золотых. Поэтому, если N – число пиратов, то разность между числом серебряных и золотых монет: 600 – 200 = 5N, откуда N = 80.
Задание 24
|
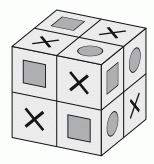
В клетках на поверхности куба 2 × 2 × 2 изображён один из трёх символов: квадрат, круг или крестик. В любых двух клетках с общей стороной находятся разные символы. На рисунке показан один из примеров. Какой из следующих наборов символов на всей поверхности куба возможен?
A) 6 кругов, 8 квадратов, остальные крестики
Б) 7 кругов, 8 квадратов, остальные крестики
В) 5 кругов, 8 квадратов, остальные крестики
Г) 7 кругов, 7 квадратов, остальные крестики
Д) ни один из предыдущих
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
Рассмотрим вершину куба 2 × 2 × 2 и три клетки на его поверхности, для
которых эта вершина является общей. Каждая из этих клеток имеет общие стороны с двумя другими. Поэтому символы на этих трёх клетках для каждой вершины куба различны. Поскольку это верно для всех 8 вершин куба (и других клеток на поверхности куба, у которых ни одна вершина не является вершиной куба, нет),
то всех трёх символов на его поверхности – поровну, т.е. по 8. Следовательно, ни один из ответов А) – Г) не является верным. Тем самым, верным является ответ Д).
Задание 25
|
Жители города всегда общаются только с помощью вопросов. При этом жители делятся на две группы: «позитивисты», на вопросы которых всегда ответом является «да», и «негативисты», на вопросы которых всегда ответом является «нет». Я встретил Альберта и Берту, и Берта спросила меня: «Я и Альберт оба негативисты?». К каким группам жителей относятся Альберт и Берта?
A) оба позитивисты
Б) оба негативисты
В) Альберт позитивист, Берта негативист
Г) Альберт негативист, Берта позитивист
Д) недостаточно информации, чтобы определить
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 47.5 - 1.25 = 46.25
|
Ясно, что Берта не может быть позитивистом. Действительно, если бы это было так, то ответ на её вопрос был бы положительными. Это, в частности, означало бы, что она негативист, противоречие. Итак, Берта – негативист, и из её вопроса следует, что они вместе с Альбертом не являются оба негативистами. Следовательно, Альберт – позитивист. Таким образом, правильным является ответ
Альберт – позитивист, Берта – негативист.
Задание 26
|
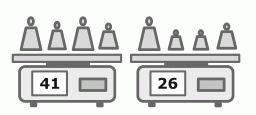
У бакалейщика имеется двенадцать гирь, массы которых выражаются целыми числами от 1 кг до 12 кг. Он распределил гири на три группы по четыре гири в каждой. Вес гирь в первой группе равен 41 кг, во второй ─ 26 кг. Какая из следующих гирь находится в одной группе с гирей весом 9 кг?
A) 3 кг Б) 5 кг В) 7 кг Г) 8 кг Д) 10 кг
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 46.25 - 1.25 = 45
|
Вес всех 12 гирь равен
1 + 2 + ... + 12 = 78 кг.
Поэтому вес третьей группы равен 78 – 41 – 26 = 11 кг. Заметим, что вес четырёх самых лёгких гирь равен
1 + 2 + 3 + 4 = 10 кг.
Поэтому единственный способ, как можно получить сумму 11, – это 1 + 2 + 3 + 5 = 11.
Далее, вес четырёх самых тяжёлых гирь равен 12 + 11 + 10 + 9 = 42. Поэтому единственный способ, как можно
получить сумму 41, – это 12 + 11 + 10 + 8 = 41. Таким образом, разбиение на группы следующее:
{1, 2, 3, 5}, {8, 10, 11, 12}, {4, 6, 7, 9}.
Видим, что из гирь, указанных в вариантах ответа, только гиря весом 7 кг находится в одной группе с гирей весом 9 кг.
Задание 27
|
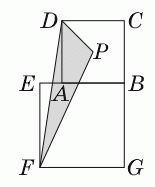
Длины диагоналей квадратов ABCD и EFGB равны 7 см и 10 см соответственно. Точка P – точка пересечения диагоналей квадрата ABCD. Чему равна площадь треугольника FPD?
A) 14,5 cм2 Б) 15 cм2 В) 15,75 cм2 Г) 16,5 cм2 Д) 17,5 cм2
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 45 + 5 = 50
|
Рассмотрим треугольник FBD. Он является прямо угольным:
∠FBD = ∠FBE + ∠EBD = 45° + 45° = 90°.
Далее, согласно условию, его катеты DB = 7 см и FB = 10 см. Поэтому его площадь
SFBD = 1/2 · 7 · 10 = 35 cм2.
Отрезок FP является медианой треугольника FBD и поэтому разбивает этот треугольник на две равновеликие части. Следовательно, площадь треугольника FPD равна
SFPD = 1/2 SFBD = 1/2 · 35 = 17,5 cм2.
Задание 28
|
Произведение цифр натурального числа N равно 20. Каким из следующих НЕ МОЖЕТ быть произведение цифр числа N + 1?
A) 40 Б) 30 В) 25 Г) 35 Д) 24
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 50 - 1.25 = 48.75
|
Так как произведение цифр числа N равно 20, число N не может иметь других цифр, кроме 1, 2, 4, 5. При добавлении 1 к числу N последняя цифра увеличится на 1, остальные цифры не изменятся. В частности, число N + 1 не может иметь цифры 7 и, значит, произведение его цифр не может равняться Г) 35 = 7 · 5. Это и есть правильный ответ.
Хотя правильный ответ уже найден, можно убедиться, что произведения цифр числа N + 1, указанные в других вариантах ответа, могли получиться. Для этого достаточно
взять значения N: А) 451, Б) 1252, В) 54, Д) 45.
Задание 29
|
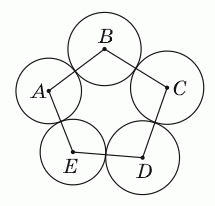
Пять соприкасающихся окружностей с центрами A, B, C, D и E расположены так, как показано на рисунке. Известно, что АВ = 16 см, ВC = 14 см, CD = 17 см, DE = 13 см, АE = 14 см. Какая точка является центром окружности наибольшего радиуса?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 48.75 - 1.25 = 47.5
|
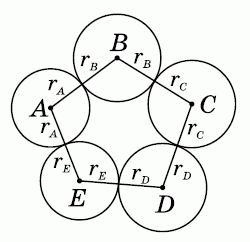
Пусть rA, rB, rC, rD, rE – радиусы окружностей с центрами A, B, C, D, E соответственно. Тогда
rA + rB = 16 см, rB + rC = 14 см, rC + rD = 17 см, rD + rE = 13 см, rE + rA = 14 см.
Сложив эти пять равенств, получим
2(rA + rB + rC + rD + rE) = 74 см,
откуда rA + rB + rC + rD + rE = 37 см
Тогда rA = (rA + rB + rC + rD + rE) – (rB + rC) – (rD + rE) = 37 – 14 – 13 = 10 см –
радиус окружности с центром A. Радиус этой окружности – наибольший, поскольку при вычислении этого радиуса из суммы всех радиусов вычитались длины наименьших сторон данного пятиугольника, а именно BC = rB + rC = 14 см и DE = rD + rE = 13 см.
Задание 30
|
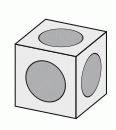
На каждой грани куба вырезано углубление в форме полушара. Эти полушары одинаковы, их центры совпадают с центрами граней, и они касаются с полушарами, вырезанными на соседних гранях. Сторона куба равна 2. Каков диаметр полушаров?
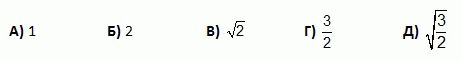
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 47.5 + 5 = 52.5
|
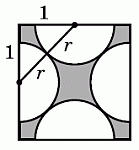
Рассмотрим сечение куба горизонтальной плоскостью, проходящей через центры боковых граней. Поскольку вырезанные шары касаются друг друга и их центры совпадают с центрами граней, в сечении получим квадрат со стороной 2, в котором вырезаны соприкасающиеся полукруги, и их центрами
являются середины сторон данного квадрата (см. рис.). Пусть r – радиус вырезанных полушаров (и, значит, вырезанных полукругов в сечении). Тогда, по теореме Пифагора, искомый диаметр