Задание 1
|

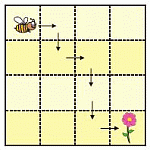
Пчёлка Бззз хочет перелететь на цветок. Какую из следующих последовательностей перелётов ей нужно совершить?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 24 + 3 = 27
|
Чтобы перелететь на цветок, пчёлке нужно переместиться на 3 клетки вниз и на 3 клетки вправо (неважно, в каком порядке). Поэтому в правильном ответе должно быть 3 стрелки вниз и 3 стрелки вправо. Во всех ответах, кроме ответа А, это условие не выполняется: в них только 5 стрелок. А путь в ответе А действительно является искомым (см. рис.).
Задание 2
|
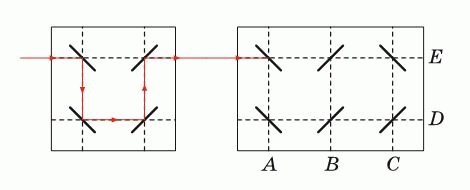
Луч лазера отражается от зеркал так, как показано на первом рисунке. В какой точке выйдет луч лазера на втором рисунке?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 27
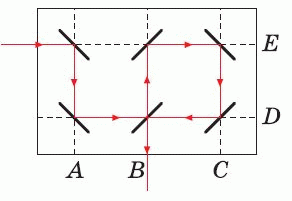
Путь луча показан на следующем рисунке. Видим, что луч выйдет в точке В.
|
Задание 3
|
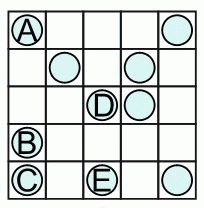
Раиса хочет, чтобы в каждой строчке и в каждом столбце следующей клетчатой доски лежало ровно 2 монеты. Какую монету ей нужно переместить в пустую клетку?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 27 - 0.75 = 26.25
|
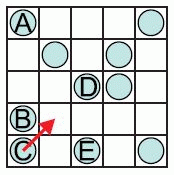
Заметим, что в левой строчке и нижнем столбце находится по 3 монеты. Поэтому нужно переместить монету, которая находится в указанных строчке и столбце, т.е. монету С. Заметим также, что во втором слева столбце и во второй снизу строчке находится по одной монете. Следовательно, монету С нужно переместить в клетку, которая является общей у этих столбца и строчки (см. рис.).
Задание 4
|
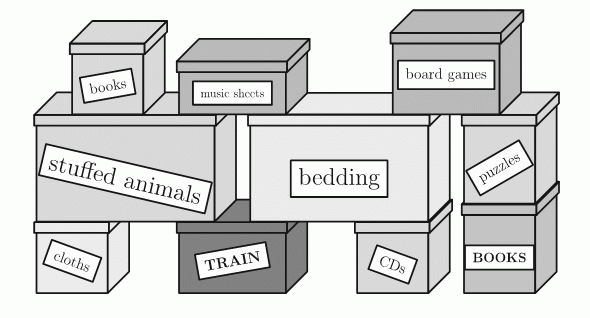
Какое наименьшее количество вышестоящих коробок нужно убрать, чтобы можно было открыть коробку с надписью «TRAIN»?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 26.25 + 3 = 29.25
|
На рисунке в условии задачи видно, что непосредственно над коробкой с надписью «TRAIN» находятся 2 коробки («stuffed animals» и «bedding»). А над этими двумя коробками находятся ещё 3 («books», «music sheets» и «board games»). Поэтому необходимо убрать по крайне мере 2 + 3 = 5 коробок.
Задание 5
|
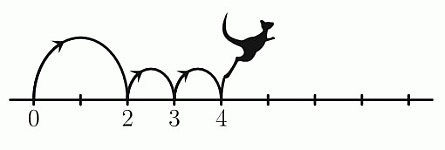
Кенгуру прыгает по прямой и делает один длинный прыжок после двух коротких, как показано на рисунке. Кенгуру начал прыгать с отметки 0 и закончил на отметке 16. Сколько прыжков он сделал?
A) 6 Б) 8 В) 10 Г) 11 Д) 12
|
Правильный ответ: Д
|
Ответ участника: БВ
|
Промежуточный результат: 29.25 - 0.75 = 28.5
|
Согласно условию, за 3 подряд прыжка кенгуру перемещается на 4 деления вправо. Такие тройки прыжков повторяются. Так как кенгуру закончил на отметке 16, то таких повторяющихся троек было 16 : 4 = 4. Следовательно, кенгуру сделал 4 · 3 = 12 прыжков.
Задание 6
|
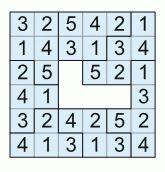
Аня хочет сложить квадрат так, чтобы в любых соседних по стороне клетках были записаны разные числа. Каким из недостающих фрагментов ей нужно воспользоваться?

|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 28.5 - 0.75 = 27.75
|
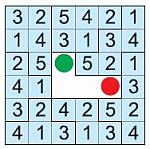
Рассмотрим крайние клетки недостающего фрагмента. Согласно условию, в клетке, отмеченной зелёным кружочком, не могут находиться числа 5 и 3. Поэтому ответ Д не является верным. Далее, в клетке, отмеченной красным кружочком, не могут находиться числа 2, 3 и 5. Поэтому ответы А, Б и В также не являются верными. Остаётся ответ Г – единственный, который может быть верным. Можно убедиться непосредственно, что он всем нужным условиям удовлетворяет.
Задание 7
|
Дано равенство:
2022 + ☐ = 2020 + ☐.
Какие из следующих чисел должны быть вписаны вместо квадратиков, чтобы оно стало правильным?
A) 3 и 5
Б) 4 и 1
В) 3 и 4
Г) 7 и 2
Д) 9 и 8
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 27.75 + 3 = 30.75
|
В левой части данного равенства первое слагаемое на 2 больше первого слагаемого в правой части равенства. Поэтому, чтобы равенство было верным, необходимо и достаточно, чтобы, наоборот, второе слагаемое в левой части было на 2 меньше, чем второе слагаемое в правой части. Такую разность имеют только числа 3 и 5. Поэтому правильным является ответ А.
Задание 8
|
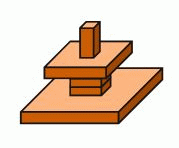
Женя построил башню, показанную на рисунке справа. Как выглядит башня, если на неё смотреть сверху?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 30.75 + 3 = 33.75
|
Если смотреть на башню сверху, то будут видны только три из пяти фигур: верхняя, вторая сверху и нижняя. Видим, что ответы А, Г и Д этому условию не удовлетворяют. Далее заметим, что горизонтальные
размеры второй (видимой сверху) фигуры являются третьими по величине и уступают только размерам самой большой нижней фигуры. Поэтому из двух оставшихся ответов верным является ответ В.
Задание 9
|

Пять автомобилей движутся в одном направлении. Сначала автомобиль 5 обогнал два автомобиля. Затем автомобиль 3 обогнал два впереди идущих автомобиля. После этого автомобиль 2 обогнал два впереди идущих автомобиля. В каком порядке движутся автомобили в результате?
A) 1, 2, 3, 5, 4
Б) 2, 1, 3, 5, 4
В) 2, 1, 5, 3, 4
Г) 3, 1, 4, 2, 5
Д) 4, 1, 2, 5, 3
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 33.75 - 1 = 32.75
|
Согласно условию задачи, порядок автомобилей во время гонки менялся так:
1, 2, 3, 4, 5 → 1, 2, 5, 3, 4 → 1, 3, 2, 5, 4 → 2, 1, 3, 5, 4.
Видим, что правильным является ответ Б.
Задание 10
|
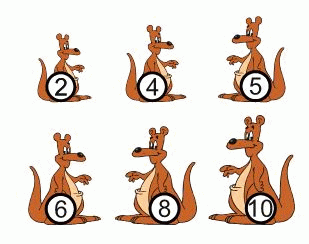
Возрасты шести кенгуру: 2, 4, 5, 6, 8 и 10 лет. Сумма лет четырёх из них равна 22 года. Сколько лет двум остальным кенгуру?
A) 2 и 8
Б) 4 и 5
В) 5 и 8
Г) 6 и 8
Д) 6 и 10
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 32.75
Сумма лет всех шести кенгуру равна 2 + 4 + 5 + 6 + 8 + 10 = 35. По условию, сумма лет четырёх из них равна 22 года. Поэтому сумма лет двух остальных кенгуру равна 35 – 22 = 13. Поскольку 13 – нечётное число, то одно из двух слагаемых, которые имеют такую сумму, также нечётное. Единственным нечётным среди данных чисел является число 5. Поэтому одному из двух рассматриваемых кенгуру 5 лет, а тогда другому 13 – 5 = 8. В результате видим, что правильным является ответ В.
|
Задание 11
|
Во время каникул я отправил своим друзьям пять открыток, показанных ниже. На открытке Мише нет уток. На открытке Кате есть солнце. На открытке Полине ровно два живых существа. На открытке Люсе изображена собака. На открытке Вите изображены кенгуру. Какую открытку получил Миша?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 32.75 + 4 = 36.75
|
Будем рассматривать утверждения задачи, начиная с последнего. На открытке Вити изображены кенгуру. Единственная открытка с кенгуру – это Б. Далее, на открытке для Люси изображена собака. Единственная открытка с собакой – это Д. На открытке для Полины ровно два живых существа. Таких открыток две: Б и В. Но открытка Б, как мы уже знаем, была отправлена Вите. Значит, Полине была отправлена открытка В. Так как, по условию, на открытке Мише нет уток, то из двух оставшихся открыток А и Г ему досталась открытка А.
Задание 12
|
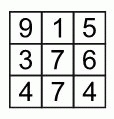
Миша хотел, заполнить клетки таблицы числами так, чтобы суммы чисел во всех строчках и столбцах были одинаковыми. Но он сделал одну ошибку. Какое число он должен исправить?
A) 1 Б) 3 В) 4 Г) 5 Д) 7
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 36.75 - 1 = 35.75
|
Вычислим суммы чисел в строчках и столбцах таблицы. Результаты указаны на рисунке справа от строчек и снизу от столбцов.
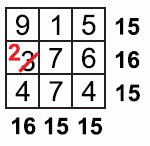
Видим, что сумма чисел в первом столбце и сумма чисел во второй строчке на 1 больше всех остальных сумм. Поэтому, чтобы суммы во всех строчках и столбцах стали одинаковыми, нужно уменьшить на 1 сумму чисел в первом столбце и второй строчке. На их пересечении находится клетка с числом 3. Следовательно, именно это число следует исправить на число 2.
Задание 13
|
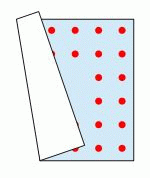
У Аладдина квадратный ковер. Вдоль каждой стороны ковра в две линии расположены одинаковые количества точек. К несчастью, ковёр завернулся как показано на рисунке. Сколько всего точек на ковре?
A) 48 Б) 44 В) 40 Г) 36 Д) 32
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 35.75 + 4 = 39.75
|
Из условия следует, что если развернуть ковёр, то он будет выглядеть так, как на рисунке.
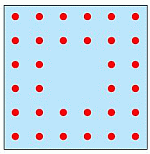
Если подсчитать количество
точек по горизонталям, то получаем сумму
6 + 6 + 4 + 4 + 6 + 6 = 32. По-другому это количество можно вычислить так. На рисунке в условии видим, что в двух крайних строчках и столбцах по 6 точек. Если бы во всех строчках и столбцах было по 6 точек, то всего их было бы 6 · 6 = 36 точек. Но на пересечении двух средних строчек и столбцов 4 точки отсутствуют. Поэтому на данном ковре их 36 – 4 = 32.
Задание 14
|
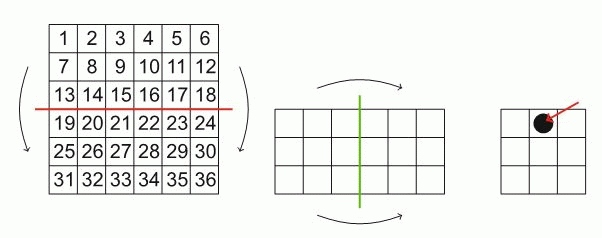
Жанна согнула квадрат с числами дважды, как показано на рисунке. Затем она проткнула сложенный квадрат в указанной точке. Какие числа записаны в клетках, которые она проткнула?
A) 8, 11, 26, 29
Б) 14, 17, 20, 23
В) 15, 16, 21, 22
Г) 14, 16, 21, 23
Д) 15, 17, 20, 22
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 39.75 + 4 = 43.75
|
После первого изгиба, в частности, наложатся друг на друга клетки с числами 14 и 20, а также клетки с числами 17 и 23. После второго изгиба все четыре указанные клетки наложатся друг на друга и окажутся в той позиции, в которой Жанна проткнула сложенный лист.
Задание 15
|
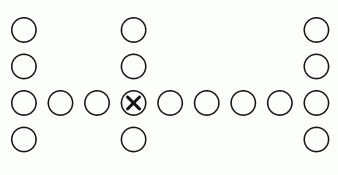
Учащиеся в классе сидят рядами. В каждом ряду одинаковое количество учеников. Перед Робертом 2 ряда учеников, а позади него – 1 ряд учеников. В его ряду 3 ученика слева от него и 5 учеников справа. Сколько учеников в этом классе?
A) 10 Б) 17 В) 18 Г) 27 Д) 36
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 43.75 + 4 = 47.75
|
Согласно условию, в классе 4 ряда сидений и в каждом ряду по 9 сидений. На рисунке крестиком указано место Роберта. Следовательно, в классе 4 · 9 = 36 учеников.
Задание 16
|
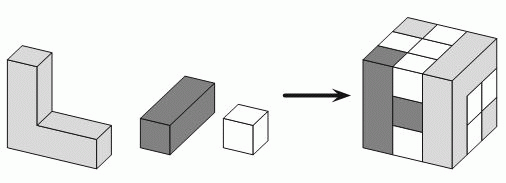
Куб построен из блоков трёх видов (см. рис.). Сколько белых блоков было при этом использовано?
A) 8 Б) 11 В) 13 Г) 16 Д) 19
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 47.75 - 1 = 46.75
|
Заметим, что весь построенный куб состоит из 3 · 3 · 3 = 27 единичных кубиков (таких, как белый блок). Серый блок состоит из 5 кубиков. На рисунке куба видно, что куб имеет 2 таких блока. Далее, чёрный блок состоит из трёх единичных кубиков. Чёрных блоков тоже 2. Поэтому серые и чёрные блоки в общей сложности состоят из 2 · 5 + 2 · 3 = 16 единичных кубиков. Тогда число белых блоков, использованных для построения куба, равно 27 – 16 = 11.
По-другому найти правильный ответ можно так. Будем подсчитывать число белых блоков по слоям, рассматривая их, например, справа. Первый (самый правый) слой полностью виден на рисунке данного
куба. Он содержит 3 белых блока. Следующие слои (средний и левый) на рисунке куба видны только частично. Но, учитывая размеры блоков, нетрудно определить, что они имеют вид такой, как на следующем рисунке.
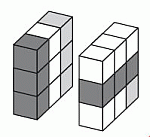
Тогда средний слой содержит 5 белых блоков, а левый слой – 3 белых блока. В результате, общее число белых блоков, использованных для построения куба, равно 3 + 5 + 3 = 11.
Задание 17
|
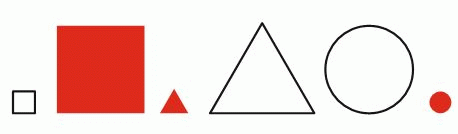
Ванда решила выбрать несколько из следующих фигур. Она хочет, чтобы среди них были 2 окрашенные фигуры, 2 большие и 2 круглые. Какое наименьшее число фигур она может выбрать, чтобы все эти условия были выполнены?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 46.75 - 1.25 = 45.5
|
Среди имеющихся фигур – только две круглые. Поэтому Ванда должна выбрать их обе. Но среди них только одна окрашенная и одна большая. Поэтому двух фигур недостаточно. А трёх фигур для выполнения условий будет достаточно, если дополнительно выбрать большой окрашенный квадрат. Таким образом, правильным является ответ Б 3.
Задание 18
|
В турнире по футболу участвуют 3 команды. Каждая команда должна сыграть с каждой другой один матч. За выигрыш в матче команда получает 3 очка, за ничью – 1 очко, а за проигрыш – ни одного очка. Какое из следующих чисел НЕ МОГЛО быть числом очков ни у одной из команд после завершения турнира?
A) 1 Б) 2 В) 4 Г) 5 Д) 6
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 45.5 - 1.25 = 44.25
|
Согласно условию, каждая команда должна сыграть два матча. В каждом матче можно получить 0, 1 или 3 очка. Поэтому общее число очков у команды после завершения турнира может быть равно только
0 = 0 + 0,
1 = 1 + 0,
2 = 1 + 1,
3 = 3 + 0,
4 = 3 + 1 и
6 = 3 + 3.
Видим, что команда не могла набрать 5 очков.
Задание 19
|
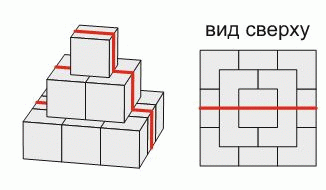
Пирамида построена из кубиков с ребром 10 см. Муравей переползает через пирамиду по красной линии, изображенной на рисунке. Какую длину имеет данный путь муравья?
A) 30 см Б) 60 см В) 70 см Г) 80 см Д) 90 см
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 44.25 - 1.25 = 43
|
Путь муравья состоит из вертикальных
и горизонтальных участков (см. рис.). Горизонтальные участки полностью видны сверху и вместе составляют переход через 3 кубика от левого края основания пирамиды до правого. Поэтому длина горизонтальной части пути равна
3 · 10 = 30 см.
Найдём длину вертикальных участков пути. Муравей 3 раза должен подняться по граням кубиков и столько же раз опуститься. Поэтому общая длина вертикальных участков пути равна
6 · 10 = 60 см.
Таким образом, длина всего пути равна 30 + 60 = 90 см.
Задание 20
|
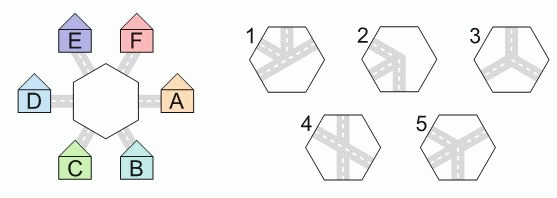
Аня хочет вложить в центр между домиками одну из плиток, указанных на рисунке справа. Она хочет при этом, чтобы от домика A можно было пройти по дорожкам к домикам B и E, но нельзя было пройти к D. Какую из плиток ей нужно выбрать. Плитки можно поворачивать.
A) 1 или 2
Б) 2 или 3
В) 1 или 4
Г) 4 или 5
Д) 1 или 5
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 43 - 1.25 = 41.75
|
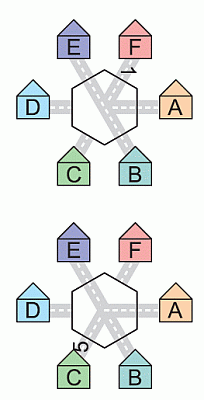
Заметим, что если можно добраться из А до В и Е, то можно добраться и от В до Е. Но домики В и Е расположены в точности напротив друг друга (на противоположных сторонах шестиугольника
в центре рисунка, куда нужно вложить плитку). Поэтому на искомой шестиугольной плитке должен быть прямой путь от одной её стороны до противоположной. Такими плитками являются плитки 1, 4 и 5. Но на плитке 4 имеются прямые пути межу двумя парами противоположных сторон. И если её положить в центре между домиками так, чтобы можно было пройти от А до В (заметим, что эти домики являются соседними), то будет прямой путь от А до D. Поэтому плитка 4 не подходит (по условию, такого пути не должно быть). А
плитки 1 и 5 всем условиям задачи удовлетворяют. Следовательно,
правильным является ответ Д.
Задание 21
|
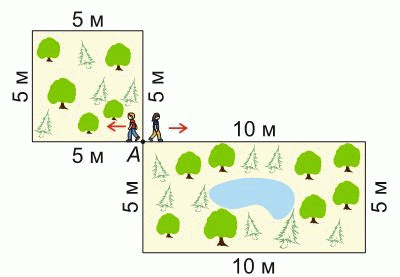
Лёша и Серёжа начинают идти из точки А вокруг квадратного и прямоугольного парков, соответственно, в указанных направлениях с одинаковой скоростью. Через некоторое время они снова встретились в точке А. Сколько раз обошёл вокруг квадратного парка Лёша до этой встречи?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 41.75 - 1.25 = 40.5
|
Периметр квадратного парка, который обходит Лёша, равен 4 · 5 = 20 метрам. Поэтому Лёша будет находиться в точке А после того, как пройдёт 20 метров, 40 метров, 60 метров, 80 метров и так далее.
Периметр прямоугольного парка, который обходит Серёжа, равен 2 · 5 + 2 · 10 = 30 метрам. Поэтому Лёша будет находиться в точке А после того, как пройдёт 30 метров, 60 метров, 90 метров и так далее. При этом, так как скорости Лёши и Серёжи одинаковые, чтобы встретиться, они должны пройти одинаковые расстояния. Видим, что наименьшее расстояние, которое они должны пройти, чтобы снова встретиться в точке А, равно 60 метрам. При этом Серёжа обойдёт свой парк 2 раза, а Лёша свой парк – 3 раза.
Задание 22
|
Пятеро девочек ели сливы. Лена съела на 2 сливы больше, чем Соня. Варя съела на 3 сливы меньше, чем Лена. Катя съела на 1 сливу больше, чем Варя, но на 3 сливы меньше, чем Алиса. Какие две девочки съели одинаковое количество слив?
A) Катя и Лена
Б) Катя и Соня
В) Лена и Алиса
Г) Соня и Алиса
Д) Алиса и Варя
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 40.5 + 5 = 45.5
|
Для наглядности построим схему, описывающую условие задачи. Стрелками укажем, кто съел слив больше, числом возле стрелки – на сколько больше.
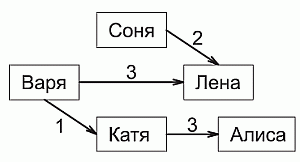
Рассмотрим на схеме Варю, Лену и Катю. Видим, что Катя съела на 3 – 1 = 2 сливы меньше, чем Лена. По условию, Соня также съела на 2 сливы меньше, чем Лена. Следовательно, Катя и Соня съели слив поровну. На схеме также видно, что других пар девочек, которые съели слив поровну, нет. В частности, Алиса съела на 1 сливу больше, чем Лена. Таким образом, правильным является ответ Б.
Задание 23
|

Маленькая «гусеница» на рисунке свернулась, чтобы заснуть. Как теперь она может выглядеть?

|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 45.5 - 1.25 = 44.25
|
Будем считать, что оранжевый кружочек – это голова гусеницы (см. рис. в условии задачи). Видим, что если двигаться вдоль гусеницы, начав с головы, то чёрные и жёлтые кружочки чередуются, начиная с чёрного. Если в варианте ответа можно построить непрерывный путь, проходящий через центры кружочков, вдоль которого цвета кружочков чередуются так же, то соответствующим образом гусеница могла свернуться. Если же такого пути не существует, то не могла. На следующем
рисунке показаны два варианта такого пути для ответа А.
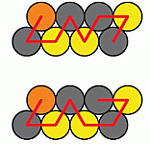
Значит, поскольку, по правилам конкурса, только один ответ может быть правильным, им является ответ А. Хотя правильный ответ найден, можно непосредственно убедиться, что в других вариантах ответа построить требуемый путь нельзя.
Задание 24
|
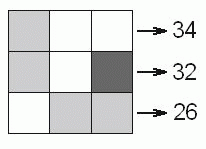
Под клетками одного и того же цвета скрыты одинаковые числа так, что суммы чисел в строчках такие, как показано на рисунке. Какое число скрыто под чёрной клеткой?
A) 6 Б) 8 В) 10 Г) 12 Д) 14
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 44.25 - 1.25 = 43
|
Будем называть числа «белыми», «серыми» и «чёрными» в соответствии с цветом клеток, под которыми они скрыты.
Рассмотрим числа в первой и третьей строчках. Если все их сложить, то это будет сумма 3 «белых» и 3 «серых» чисел. И эта сумма равна 34 + 26 = 60. Тогда сумма одного «белого» и одного «серого» числа равна 60 : 3 = 20. Во второй строчке – по одному числу каждого цвета. Так как сумма первых двух из них равна 20, а сумма всех трёх равна 32, чёрное число равно 32 – 20 = 12.
По-другому, но немного длиннее, можно решить задачу так. Найдём сначала значения «белого» числа и «серого» числа. Заметим, что если в первой строчке заменить одно «белое» число на «серое», то получится такой же набор чисел, как в третьей строчке. При этом сумма чисел в строчке уменьшится на 34 – 26 = 8. Следовательно, «белое» число на 8 больше «серого» числа. Поэтому, если в первой строчке заменить «серое» число на «белое», то получим, что сумма трёх белых чисел равна 34 + 8 = 42. Тогда одно «белое» число равно 42 : 3 = 14. Аналогично, если в третьей строчке заменить одно «белое» число на «серое», то получим 3 «серых» числа, сумма которых равна 26 – 8 = 18. Тогда одно «серое» число равно 18 : 3 = 6. В результате, рассматривая вторую строчку, находим, что «чёрное» число равно 32 – 14 – 6 = 12.