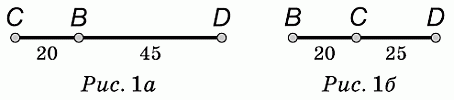Задание 1
|
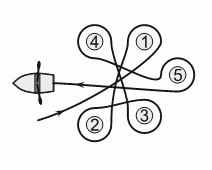
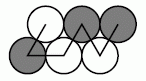
Миша проплыл на лодке вокруг пяти буёв, как показано на рисунке. Какие буи он огибал по ходу часовой стрелки?
A) 2, 3 и 4
Б) 1, 2 и 3
В) 1, 3 и 5
Г) 2, 4 и 5
Д) 2, 3 и 5
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 30 - 0.75 = 29.25
|
Двигаясь вдоль указанного пути, отметим стрелками направления поворота вокруг буёв.
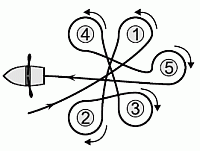
Видим, что по ходу часовой стрелки лодка огибала буи 2, 3 и 5.
Задание 2
|
Света хочет сложить в некотором порядке следующие 5 карточек с числами так, чтобы у неё получилось наименьшее возможное 9-значное число. Какую карточку ей нужно положить на краю справа?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Чтобы число из некоторого набора цифр было наименьшим, необходимо, чтобы на старшие разряды приходились как можно меньшие цифры, т.е. цифры (слева направо) должны располагаться в порядке неубывания. Но в данном случае не на всех карточках изображены цифры. На трёх карточках записаны многозначные числа. Цифры на них нельзя поменять местами, тем более использовать отдельно. Поэтому, чтобы составить из карточек наименьшее число, нужно расположить карточки в порядке неубывания первых цифр на этих карточках. (В случае совпадения первых цифр такое же правило следует применить для вторых цифр и т.д. Но у нас таких совпадений нет.) Поэтому последней должна быть карточка с
наибольшей первой цифрой, т.е. карточка 
Хотя правильный ответ уже найден, укажем расположение всех карточек, дающее наименьшее число:
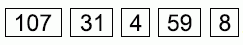
Задание 3
|
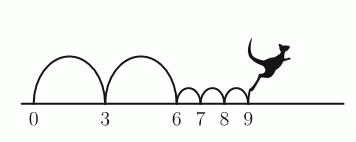
Кенгуру прыгает вдоль числовой прямой, начав с числа 0. Он чередует длинные и короткие прыжки. После двух длинных прыжков он делает три короткие, затем – снова два длинные, три короткие и т.д. На какое из следующих чисел выпадет прыжок кенгуру?
A) 82 Б) 83 В) 84 Г) 85 Д) 86
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 32.25 + 3 = 35.25
|
После каждой серии повторяющихся прыжков кенгуру перемещается на 9 единиц вперёд (см. рисунок). Поэтому после 9 таких серий он окажется на позиции 9 · 9 = 81, после чего начнётся новая серия с двух длинных прыжков. После первого из них кенгуру окажется на позиции 81 + 3 = 84, а после второго – на позиции 84 + 3 = 87. Видим, что из приведённых вариантов ответа
только на число 84 приходится один из прыжков кенгуру.
Задание 4
|
У автомобиля Кенгуру отвалился номер. Кунгуру прикрепил его на место, но перепутал верх и низ. Однако, номер стал читаться так же, как и раньше. Каким из следующих мог быть номер автомобиля Кенгуру?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 35.25 + 3 = 38.25
|
Ниже показано, как выглядят перевёрнутые номера.
A) 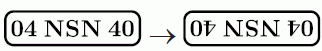
Б) 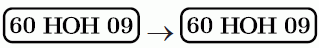
В) 
Г) 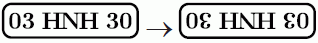
Д) 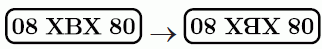
Видим, что только в варианте Б прочтение номера после переворачивания не меняется.
Задание 5
|
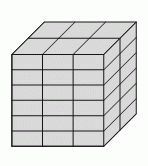
У Роба Билдера есть кирпичи. Меньшая их сторона равна 4 см. Роб сложил из таких кирпичей куб так, как показано на рисунке. Какие размеры (в см) имеют кирпичи?
A) 4 × 6 × 12
Б) 4 × 6 × 16
В) 4 × 8 × 12
Г) 4 × 8 × 16
Д) 4 × 12 × 16
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 38.25 + 3 = 41.25
|
По условию задачи, высота кирпича равна 4 см. Куб состоит из 6 слоёв такой высоты (см. рисунок). Следовательно, длина ребра куба равна 6 · 4 = 24 см. Такое ребро «образуют» 3 кирпича по его ширине или 2 кирпича по его длине. Поэтому ширина кирпича равна 24 : 3 = 8 см, а длина – 24 : 2 = 12 см. Таким образом, размеры кирпича (в см): 4 × 8 × 12.
Задание 6
|
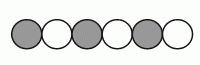
Черно-белая гусеница (см. рис.) свернулась калачиком. Как теперь она может выглядеть?
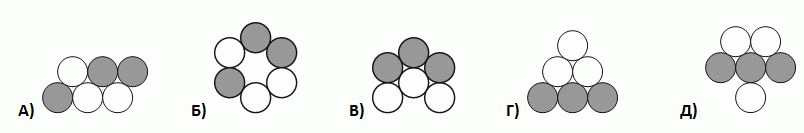
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
На рисунке в условии задачи видно, что если двигаться вдоль гусеницы, то чёрные и белые кружочки чередуются. Если в варианте ответа можно построить непрерывный путь, проходящий через центры кружочков, вдоль которого цвета кружочков также чередуются, то в свёрнутом виде гусеница может выглядеть так, как указано в данном ответе. Если же такого пути не существует, то не может. В варианте ответа А такой путь существует.
Можно убедиться, что в других вариантах ответа такие пути построить нельзя.
Задание 7
|

В следующем выражении 5 пустых клеток. Саня хочет вписать в них четыре знака плюс и один знак минус так, чтобы получилось правильное равенство. В какую клетку ей следует вписать знак минус?
A) между 6 и 9
Б) между 9 и 12
В) между 12 и 15
Г) между 15 и 18
Д) между 18 и 21
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Если поставить все знаки «+», то получим сумму
6 + 9 + + 12 + 15 + 18 + 21 = 81.
Поэтому нужно поменять один знак «+» на знак «–» так, чтобы сумма уменьшилась на 81 – 45 = 36. Заметим, что если просто в сумме убрать какое-то слагаемое, то и сумма уменьшится на значение, равное этому слагаемому. Если же оставить данное слагаемое, но заменить знак «+» на «–», то сумма уменьшится на величину, в два раза большую этого слагаемого. Поэтому, чтобы получить нужное равенство, нужно поставить знак «–» перед числом 36 : 2 = 18. Действительно, равенство
6 + 9 + 12 + 15 – 18 + 21 = 45
является верным.
Задание 8
|
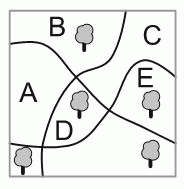
В парке растут 5 деревьев и имеется 3 дорожки (см. рис.). В какой части парка следует посадить ещё одно дерево, чтобы у каждой дорожки с обеих сторон было одинаковое количество деревьев?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 43.5 - 0.75 = 42.75
|
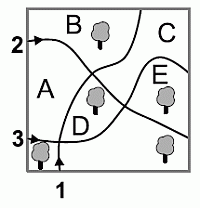
Рассмотрим путь 1. Если идти по нему в указанном направлении, то слева мы насчитаем 2 дерева, а справа – 3. Поэтому дерево следует посадить слева по этому пути, т.е. в части А или В.
Если идти по пути 2 в указанном направлении, то также слева будет 2 дерева, а справа – 3. Поэтому дерево следует посадить слева по этому пути, т.е. в части В, С или Е. Видим, что оба эти условия будут выполнены, если дерево посадить
в части В.
Можно убедиться, что тогда и для пути 3 с обеих сторон будет по 3 дерева.
Задание 9
|
Сколько чисел от 100 до 300 состоят только из нечётных цифр?
A) 25 Б) 50 В) 75 Г) 100 Д) 150
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 42.75 - 0.75 = 42
|
Нечётными цифрами являются цифры 1, 3, 5, 7 и 9. Всего их пять. Но чтобы получилось нечётное число от 100 до
300, первой должна быть цифра 1. Второй и третьей может быть любая из пяти нечётных цифр. Поэтому общее количество таких чисел равно 1 · 5 · 5 = 25.
Задание 10
|

Жора вычислил сумму квадратов двух чисел. К сожалению, на бумагу пролились чернила и некоторые цифры оказались скрыты. Какой цифрой заканчивается первое число?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Г
|
Промежуточный результат: 42 - 0.75 = 41.25
|
Так как второе число заканчивается цифрой 2, то его квадрат заканчивается цифрой 4. Тогда квадрат первого числа должен заканчиваться цифрой 9 – 4 = 5. А отсюда следует, что и само первое число должно заканчиваться цифрой 5.
Покажем, что описанная в условии ситуация действительно возможна (для решения задачи это не обязательно):
23852 + 12022 = 7133029.
Задание 11
|
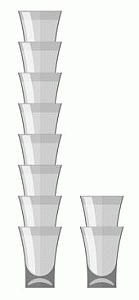
Расстояние между двумя полками в кухонном шкафу Моники составляет 36 см. Она знает, что стопка из 8 её стаканов имеет высоту 42 см, а стопка из 2 стаканов – 18 см (см. рис.). Какое наибольшее число стаканов Моника может собрать в стопку, чтобы её можно было поставить на полку в шкафу?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 41.25 + 4 = 45.25
|
Стопка из 8 стаканов имеет высоту 42 см, а стопка из 2 стаканов – высоту 18 см. Это значит, что при увеличении стопки на 8 – 2 = 6 стаканов её высота увеличивается на 42 – 18 = 24 см. Следовательно, при увеличении стопки на 1 стакан высота увеличивается на 24 : 6 = 4 см.
Получаем, если стопку из 8 стаканов уменьшить на 1 стакан, её высота станет равна 42 – 4 = 38 см. Такая стопка не помещается в шкаф, так как расстояние между полками меньше.
Если же убрать ещё 1 стакан, то получим стопку из 6 стаканов, высота которой будет равна 38 – 4 = 34 см. Такая стопка помещается в шкаф. Таким образом, правильным является ответ 6.
Задание 12
|
У стандартного игрального кубика количество точек на противоположных гранях равно 7. Четыре стандартных кубика склеили так, как показано на рисунке. Какое наименьшее количество точек может быть на поверхности полученной фигуры?
A) 52 Б) 54 В) 56 Г) 58 Д) 60
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 45.25 - 1 = 44.25
|
Количество точек на всех шести гранях каждого стандартного кубика равно
1 + 2 + 3 + 4 + 5 + 6 = 21.
Тогда количество точек на всех гранях четырёх кубиков равно 21 · 4 = 84. Ясно, что количество точек на поверхности фигуры, склеенной из этих кубиков, будет наименьшим, если количество точек на склеенных гранях будет наибольшим. У двух средних кубиков склеены по две противоположные грани. По условию, независимо от того, какие это грани, количество точек на них равно 7 + 7 = 14. Наибольшее количество точек на склеенных гранях каждого из крайних кубиков равно 6. Поэтому наибольшее количество точек на всех склеенных гранях равно 14 + 6 + 6 = 26. Следовательно, наименьшее количество точек на поверхности данной фигуры равно 84 – 26 = 58.
Задание 13
|
Средний возраст трёх сестёр составляет 10 лет. Если считать их возраст парами, то в двух из пар средний возраст равен 11 и 12 лет. Сколько лет старшей из сестёр?
A) 10 Б) 11 В) 12 Г) 14 Д) 16
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 44.25 + 4 = 48.25
|
Определим возрасты всех трёх сестёр. Если средний возраст трёх сестёр равен 10 лет, то им вместе 10 · 3 = 30 лет.
Так как средний возраст первой пары равен 11 годам, то вместе двум сёстрам этой пары 11 · 2 = 22 года. Тогда сестре, которая не вошла в эту пару, 30 – 22 = 8 лет.
Аналогично, так как средний возраст второй пары равен 12 годам, то вместе двум сёстрам этой пары 12 · 2 = 24 года. Тогда сестре, которая не вошла в эту пару, 30 – 24 = 6 лет.
Наконец, возраст третьей сестры равен 30 – 8 – 6 = 16 лет. Видим, что она самая старшая, и в результате правильным является ответ 16.
Задание 14
|
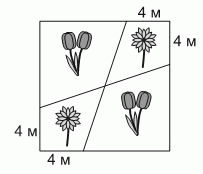
Садовник Тони посадил тюльпаны  и ромашки
и ромашки  на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?
на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?
A) 48 м2 Б) 46 м2 В) 44 м2 Г) 40 м2 Д) 36 м2
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 48.25 + 4 = 52.25
|
Легко видеть, что две части клумбы, на которых растут ромашки, одинаковые
и их общая точка – это центр данного квадрата. Поэтому перпендикуляры, опущенные из этой точки на стороны данного квадрата, разбивают его
на 4 квадрата со стороной 6 м.
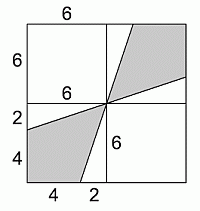
Площадь одного такого квадрата равна 36 м2. Тот квадрат, который содержит участок с ромашками, состоит ещё из прямоугольных треугольников с катетами 6 и 2. Их суммарная площадь равна 12 м2. Поэтому площадь одного участка с ромашками равна
36 – 12 = 24 м2. А тогда площадь двух частей клумбы, на которых посажены ромашки, равна 2 · 24 = 48 м2.
Задание 15
|
В моём кабинете двое настенных часов. Одни спешат на 1 минуту в час, а другие на 2 минуты в час отстают. Вчера я установил правильное время на обоих часах. Но сегодня, когда я посмотрел на часы, то обнаружил, что одни часы показывают 11:00, а другие 12:00. Когда вчера я установил время на часах?
A) 23:00 Б) 19:40 В) 15:40 Г) 14:00 Д) 11:20
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 52.25 - 1 = 51.25
|
Так как одни часы каждый час спешат на 1 минуту, а другие отстают на 2 минуты, то каждый час разница в показаниях часов увеличивается на 1 + 2 = 3 минуты. Поэтому, если разница в показаниях за какое-то время оказалась равна
1 час, т.е. 60 минут, то с момента установки правильного времени прошло 60 : 3 = 20 часов. За это время часы, которые спешат, ушли вперёд на 20 мин. Поэтому точное время на данный момент: 12:00 – 0:20 = 11:40. Понятно, что 24 часа назад точное время было
таким же. А тогда 20 часов назад (в момент установки часов), т.е. через 24 – 20 = 4 часа после этого, время было 11:40 + 4:00 = 15:40.
Задание 16
|
Ваня записал на доске несколько натуральных чисел, меньших 7. Рита стёрла все эти числа и каждое число Вани заменила числом, которое получится, если от 7 отнять число Вани. Сумма чисел, записанных Ваней, равнялась 22, сумма чисел, записанных Ритой, оказалась равна 34. Сколько чисел записал на доске Ваня?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 51.25 + 4 = 55.25
|
Сумма всех чисел, записанных Ваней и Ритой, равна 22 + 34 = 56. В то же время, если рассмотреть пару чисел (число Вани a и число 7 – a, которое записала вместо него Рита), то
видим, что сумма чисел такой пары равна a + (7 – a) = 7. Все числа
Вани и Риты разбиваются на такие пары. Поэтому количество пар равно 56 : 7 = 8. Следовательно, Ваня записал 8 чисел.
Задание 17
|
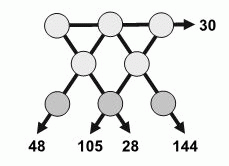
Числа от 1 до 8 вписаны в кружочки на рисунке (каждое ровно один раз). Произведения троек чисел, расположенных на одной прямой, указаны на данном рисунке. Чему равна сумма трёх чисел в нижнем ряду?
A) 11 Б) 12 В) 15 Г) 17 Д) 19
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 55.25 + 4 = 59.25
|
Начнём с того, что имеется ровно два произведения (30 и 105), которые делятся на 5. Поэтому на пересечении соответствующих этим произведениям прямых должно быть записано число 5. В свою очередь, только произведения 105 и 28 делятся на 7. Поэтому на пересечении соответствующих прямых должно быть число 7. Тогда произведение 105 дают числа 5, 3, 7 (сверху вниз в указанном порядке).
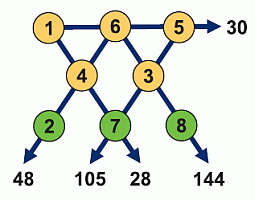
Далее, произведение 28 делится на 4. Поэтому на соответствующей прямой, помимо числа 7, должны быть числа 1 и 4 (по условию, среди данных чисел только одно число 2). Так как произведение 30 не делится на 4, то произведение 28 дают числа 1, 4, 7 (в указанном порядке сверху вниз).
Теперь, так как крайние числа в верхнем ряду – это 1 и 5, между ними должно быть число 30 : (1 · 5) = 6.
Наконец, два крайних числа в нижнем ряду – это 48 : (6 · 4) = 2 и
144 : (6 · 3) = 8. Таким образом, сумма трёх чисел в нижнем ряду равна 2 + 7 + 8 = 17.
Задание 18
|
Площадь пересечения круга и треугольника составляет 45% от площади их объединения. Площадь части треугольника вне круга составляет 40% от площади их объединения. Сколько (по площади) процентов круга лежит за пределами треугольника?
A) 20% Б) 25% В) 30% Г) 35% Д) 50%
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 59.25 + 4 = 63.25
|
Примем площадь объединения за 100 (квадратных единиц). Тогда, согласно условию, площадь пересечения равна 45, а площадь части треугольника вне круга равна 40.
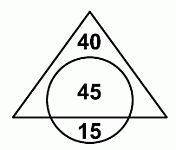
Поэтому площадь круга вне треугольника равна 100 – 45 – 40 = 15, а площадь всего круга равна 45 + 15 = 60. В результате, часть круга вне треугольника составляет 15/60 · 100% = 25%.
Задание 19
|
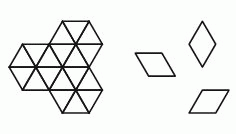
Сколько существует различных способов замощения следующей фигуры указанными на рисунке ромбиками?
A) 1 Б) 6 В) 8 Г) 9 Д) 12
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 63.25 - 1 = 62.25
|
Существует 3 способа покрыть ромбиком треугольник А.
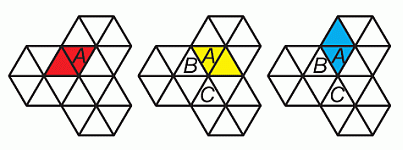
В первом случае дальнейшее замощение продолжается однозначно. Во втором и третьем случае существует 4 способа продолжения замощения. Действительно, имеется две возможности покрыть
треугольник В и при каждой из
них – две возможности покрыть треугольник С. Таким образом, существует 1 + 4 + 4 = 9 способов замощения данной фигуры указанными ромбиками.
Задание 20
|
Марк всегда ездит на велосипеде с одной и той же скоростью и ходит с одной и той же скоростью. На расстояние от дома до школы и обратно на велосипеде ему нужно 20 минут, а на такое же расстояние пешком ─ 60 минут. Вчера Марк поехал в школу на велосипеде, но оставил его у дома Евы и дальше пошёл пешком. На обратном пути он дошел до дома Евы и дальше поехал на велосипеде. На этот раз на всю дорогу от дома до школы и обратно Марку понадобилось 52 минуты. Какую часть пути Марк ехал на велосипеде?
A) 1/6 Б) 1/5 В) 1/4 Г) 1/3 Д) 1/2
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 62.25 - 1 = 61.25
|
Примем весь путь до школы и обратно за 1. Пусть x – часть
пути, которую Марк ехал на велосипеде. Тогда (1 – x) – часть пути, которую он шёл пешком. Поэтому время на весь путь смешанным способом можно представить в виде
20x + 60(1 – x).
Согласно условию, получаем уравнение
20x + 60(1 – x) = 52.
Упрощая уравнение, получаем: 60 – 40x = 52, или 40x = 8, откуда x = 1/5.
Задание 21
|

Аня решила вписать числа в клетки таблицы 3 × 3 так, чтобы суммы чисел во всех квадратах 2 × 2 были одинаковыми. Три числа она уже вписала так, как показано на рисунке. Какое число должно быть вписано в клетку, отмеченную знаком вопроса?
A) 0 Б) 1 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 61.25 + 5 = 66.25
|

Рассмотрим два верхних квадрата 2 × 2. Две
клетки в среднем столбце у этих квадратов общие. Поэтому суммы чисел в этих квадратах будут одинаковыми,
если 2 + a = 4 + b, откуда a = b + 2. Теперь рассмотрим два нижних квадрата 2 × 2. Точно так же суммы чисел в них будут равны, если ? + a = b + 3, т.е. если ? + (b + 2) = b + 3, откуда ? = 1.

По-другому правильный ответ можно найти так. По условию, суммы чисел во всех квадратах 2 × 2 должны быть равны. Тогда
(2 + c + a + e) + (e + b + d + 3) = (c + 4 + e + b) + (a + e + ? + d).
Взаимно уничтожая одинаковые слагаемые в обеих частях данного равенства, получим 2 + 3 = 4 + ?, откуда ? = 1.
Задание 22
|
Деревни A, B, C и D расположены (в каком-то порядке) вдоль длинной прямой дороги. Расстояние между A и C равно 75 км, расстояние между B и D – 45 км, а между B и C – 20 км. Каким из следующих НЕ МОЖЕТ быть расстояние между A и D?
A) 10 км Б) 50 км В) 80 км Г) 100 км Д) 140 км
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 66.25 - 1.25 = 65
|
Рассмотрим сначала деревни B, C и D. Есть две возможности: либо деревня B расположена между C и D (см. рис. 1а), либо нет (см. рис. 1б). Во втором случае расстояние между C и D равно 45 – 20 = 25 км.
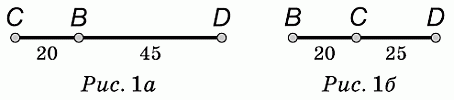
Теперь рассмотрим местоположение деревни А.
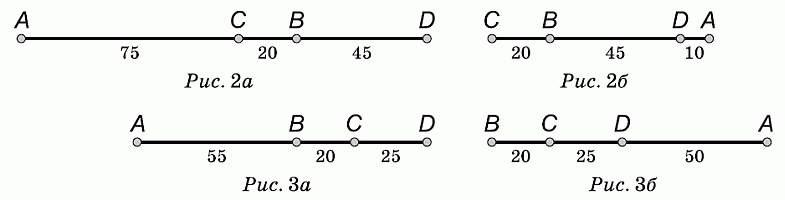
В каждом из рассмотренных случаев есть две возможности: либо она расположена (по условию, на расстоянии 75 км) слева от С, либо – справа (см. рис. 2а, 2б, 3а, 3б). Таким образом, расстояние между A и D может принимать, соответственно, следующие значения: 140 км, 10 км, 100 км и 50 км. Следовательно, среди предложенных вариантов ответа правильным является ответ 80 км.
Задание 23
|
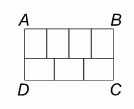
Прямоугольник ABCD состоит из семи меньших равных прямоугольников (см. рис.). Чему равно отношение AB : BC?
A) 1/2 Б) 3/4 В) 8/5 Г) 12/7 Д) 7/3
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 65 - 1.25 = 63.75
|
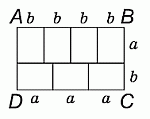
Пусть прямоугольник ABCD составлен из прямоугольников размера a × b. Тогда 3a = 4b, откуда a = 4/3 b. Тогда
AB : BC = (4b) : (a + b) = (4b) : (7/3 b) = 4/1 : 7/3 = 12/7.
Задание 24
|
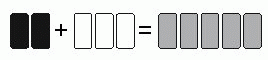
Художник хотел смешать 2 литра чёрной краски с 3 литрами белой краски, чтобы получилось 5 литров серой краски. Однако, по ошибке он смешал 3 литра чёрной с 2 литрами белой. В результате получился неправильный оттенок серого цвета. Какое наименьшее количество этой серой краски нужно отлить, чтобы в остаток этой краски можно было добавить некоторое количество белой краски и получить 5 литров серой краски нужного оттенка?
A) 5/3 литра Б) 3/2 литра В) 2/3 литра Г) 3/5 литра Д) 5/9 литра
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 63.75 - 1.25 = 62.5
|
В полученной неправильной смеси 1 лишний литр чёрной краски. Поэтому нужно отлить столько неправильной серой краски, чтобы при этом из раствора изъять 1 литр чёрной краски. В неправильном растворе в каждом литре содержится 3/5 чёрной краски. Поэтому, чтобы отлить 1 литр чёрной краски из этого раствора, нужно отлить 1 : 3/5 = 5/3 литра раствора.
Несколько по-другому ответ можно получить так. Нужно уменьшить объём чёрной краски на 1 литр из 3, т.е. на 1/3. Тогда и все 5 литров объёма неправильного раствора нужно уменьшить на треть, т.е. нужно отлить 5/3 литра раствора.
Задание 25
|
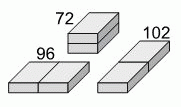
У строителя есть два одинаковых кирпича. Если сложить их тремя разными способами, как показано на рисунке, то получатся блоки, площади поверхности которых равны 72 см2, 96 см2 и 102 см2. Чему равна площадь поверхности одного такого кирпича?
A) 36 см2 Б) 48 см2 В) 52 см2 Г) 54 см2 Д) 60 см2
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 62.5 + 5 = 67.5
|
Пусть площади поверхности разных граней кирпича равны А, В и С.
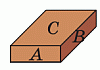
Тогда
4A + 4B + 2C = 72,
4A + 2B + 4C = 96,
2A + 4B + 4C = 102.
Сложив все эти три уравнения, получим
10(A + B + C) = 270.
Тогда площадь поверхности одного кирпича равна
2(A + B + C) = 270 : 5 = 54 см2.
Задание 26
|

Какое наименьшее количество клеток нужно окрасить в квадрате 5 × 5, чтобы в любом прямоугольнике 1 × 4 и 4 × 1, состоящем из четырёх клеток, была хотя бы одна окрашенная клетка?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 67.5 - 1.25 = 66.25
|
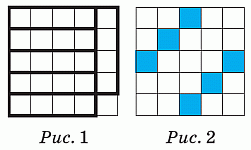
В квадрате можно выделить 6 непересекающихся прямоугольников 1 × 4 и 4 × 1 (см. рис.1). Поэтому не менее 6 клеток должны быть окрашены.
С другой стороны, если окрасить 6 клеток так, как показано на рис.2, то все условия будут выполнены. Следовательно, правильным является ответ 6.
Задание 27
|
Маугли спрашивает зебру и пантеру, какой сегодня день. Зебра всегда врёт в понедельник, вторник и среду. Пантера всегда врёт в четверг, пятницу и субботу. Зебра говорит: «Вчера был один из дней, когда я вру». Пантера говорит: «Вчера тоже был один из дней, когда я вру». Какой сегодня день?
A) четверг Б) пятница В) суббота Г) воскресенье Д) понедельник
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 66.25 - 1.25 = 65
|
Если сегодня зебра говорит правду, то в предшествующий день она, действительно, врёт. Поэтому сегодня может быть только четверг. Если же зебра сегодня врёт, то предшествующий день должен быть днём, когда она говорит правду. Поэтому сегодня может быть только понедельник. Итак, по ответу зебры Маугли может заключить, что сегодня либо четверг, либо понедельник.
Аналогично, из ответа пантеры следует, что сегодня либо воскресенье (если пантера говорит правду), либо четверг (если пантера врёт).
Чтобы оба утверждения (и пантеры, и зебры) соответствовали условию задачи, сегодня должен быть день, который назвали и зебра, и пантера. Следовательно, сегодня четверг.
Задание 28
|
На прямой было отмечено несколько точек. Роман между любыми двумя соседними отмеченными точками отметил ещё по одной точки. Затем он повторил эту процедуру ещё 3 раза. В результате получилось 225 отмеченных точек. Сколько отмеченных точек было вначале?
A) 10 Б) 12 В) 15 Г) 16 Д) 25
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 65 + 5 = 70
|
Пусть в начале на прямой было отмечено n точек. Тогда между соседними точками было (n – 1) промежутков. Поэтому на первом шаге Роман отметил (n – 1) точку, и их стало (2n – 1).
Аналогично, после второго шага их стало
2(2n – 1) – 1,
после третьего шага их стало
2(2(2n – 1) – 1) – 1,
наконец, после четвёртого шага их стало
2(2(2(2n – 1) – 1) – 1) – 1.
Раскрыв скобки, получим 16n – 15. Согласно условию, имеем уравнение 16n – 15 = 225, из которого n = 15.
Задание 29
|
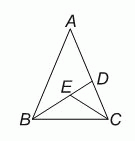
Равнобедренный треугольник АВС (АВ = АС) разрезали на три меньших равнобедренных треугольника, как показано на рисунке. При этом AD = DB, CE = CD = ВE. Найдите величину угла BAC.
A) 24° Б) 28° В) 30° Г) 35° Д) 36°
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 70 + 5 = 75
|
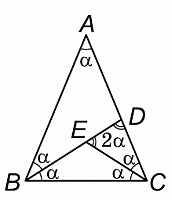
Пусть искомый угол BAC равен α. По условию, треугольник ABD – равнобедренный. Поэтому ∠ABD = ∠BAD = α. Тогда
∠BDC = ∠ABD + ∠BAD = 2α
(как внешний угол треугольника ABD).
Так как, по условию, и треугольник EDC равнобедренный, его угол ∠DEC также равен 2α. Но этот угол является внешним углом равнобедренного треугольника BEC. Поэтому его внутренние углы ∠CBE = ∠BCE = (2α) : 2 = α. Тогда ∠ABC = 2α.
Так как треугольник ABC равнобедренный, его угол ∠ACB также равен 2α. Подсчитывая сумму углов треугольника ABC, получаем уравнение
α + 2α + 2α = 180°,
или 5α = 180°, откуда α = 36°.
Задание 30
|
В семи парках обитает 2022 кенгуру и несколько коал. В каждом парке количество кенгуру равно общему количеству коал во всех остальных парках. Сколько всего коал обитает во всех семи парках?
A) 288 Б) 337 В) 576 Г) 674 Д) 2022
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 75 - 1.25 = 73.75
|
Пусть в парке номер n обитает Kn кенгуру и Cn коал. По условию,
K1 + K2 + K3 + K4 + K5 + K6 + K7 = 2022.
Пусть С = С1 + С2 + С3 + С4 + С5 + С6 + С7 – количество коал во всех семи парках. Согласно условию, справедливы 7 равенств:
K1 = C – C1, K2 = C – C2, K3 = C – C3, K4 = C – C4, K5 = C – C5, K6 = C – C6, K7 = C – C7.
Сложив их, получим:
K1 + K2 + K3 + K4 + K5 + K6 + K7 = 7С – (С1 + С2 + С3 + С4 + С5 + С6 + С7),
или 2022 = 6C, откуда C = 2022 : 6 = 337.







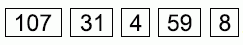


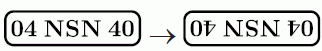
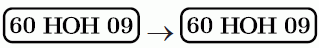

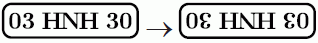


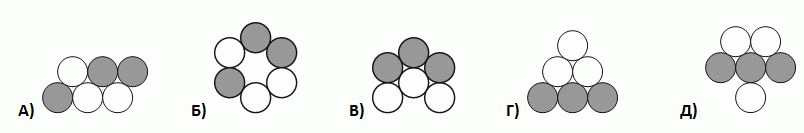








 и ромашки
и ромашки  на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?
на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?