Опубликованы результаты конкурса "Кенгуру-2015"
 |
Подведены итоги конкурса "Кенгуру-2015". Международная математическая игра-конкурс "Кенгуру-2015" проводилась 19 марта 2015 года. 127 524 учащихся из 2 792 учреждений образования Республики Беларусь приняли участие в самом массовом математическом соревновании школьников в мире. |
В один день ребята из Армении, Австрии, Бельгии, Болгарии, Бразилии, Беларуси, Канады, Швейцарии, Кипра, Чешской Республики, Германии, Эквадора, Эстонии, Испании, провинции Каталония, Финляндии, Франции, Грузии, Греции, Хорватии, Венгрии, Индонезии, Ирана, Италии, Кыргызстана, Казахстана, Колумбии, Литвы, Молдовы, Македонии, Мексики, Монголии, Нидерландов, Норвегии, Республики Берег Слоновой Кости, Пакистана, Польши, Пуэрто-Рико, Португалии, Парагвая, Румынии, Сербии, России, Швеции, Словении, Словакии, Туниса, Украины, Великобритании, Соединенных Штатов Америки, Венесуэлы, Чили, Ганы, Ирландии, Израиля, Коста-Рики, Латвии и Малайзии пробовали свои силы в решении оригинальных математических задач.
В нашей стране наиболее массово в этом интеллектуальном соревновании участвовали учащиеся столичных учреждений образования. Более 28 тысяч юных минчан старались решить как можно больше интересных нестандартных задач. По сравнению с «Кенгуру-2014» в конкурсе 2015 года общее количество участников уменьшилось на 5585. Уменьшение количества участников произошло во всех регионах. По регионам участники распределились следующим образом:
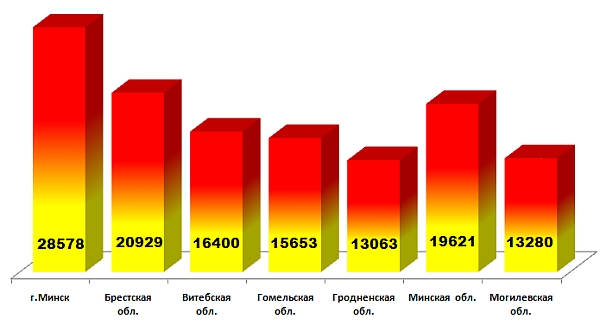
Ребята из всех стран выполняли практически одинаковые задания. С учётом национальных программ изучения математики оргкомитеты имеют право заменить не более пяти вопросов в одном из шести заданий, которые готовятся лучшими учителями и преподавателями математики, и утверждаются на ежегодной рабочей встрече представителей стран-участниц, которую организует Ассоциация «Кенгуру» без границ». Задания разрабатываются для шести возрастных групп: учащихся 1-2-х, 3-4-х, 5-6-х, 7-8-х, 9-10-х и 11-х классов. Распределение участников в соответствии с классами следующее:
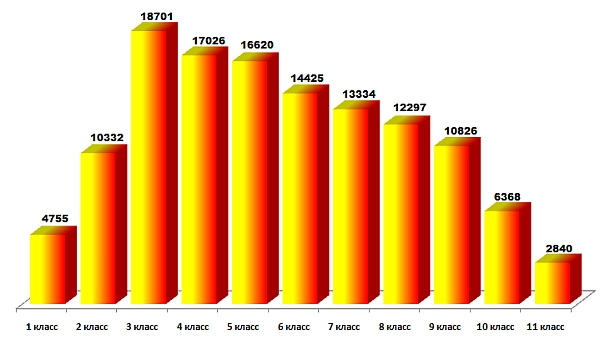
Напомним, что все задачи в задании условно разделены на три уровня сложности: вопросы легкие, каждый из которых оценивается в 3 балла; задачи среднего уровня сложности, которые оцениваются в 4 балла; и, наконец, сложные, нестандартные задачи, для решения которых надо проявить смекалку, умение рассуждать, анализировать, оцениваются в 5 баллов. Успешность выполнения заданий, т.е. процент участников правильно ответивших на каждый вопрос задания, для каждого возрастного уровня отражена на следующих диаграммах.
Диаграмма успешности выполнения задания для 1-2-х классов:
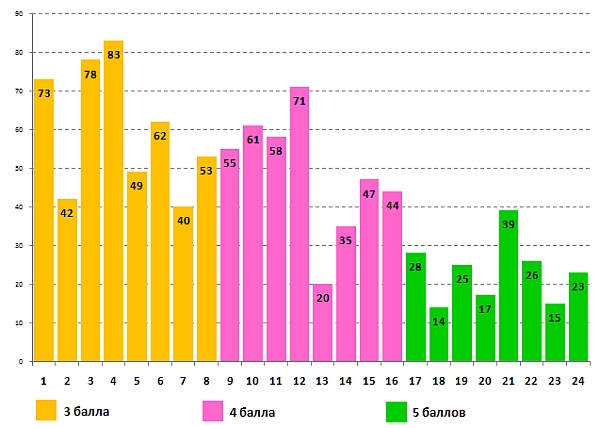
Диаграмма для 3-4-х классов:
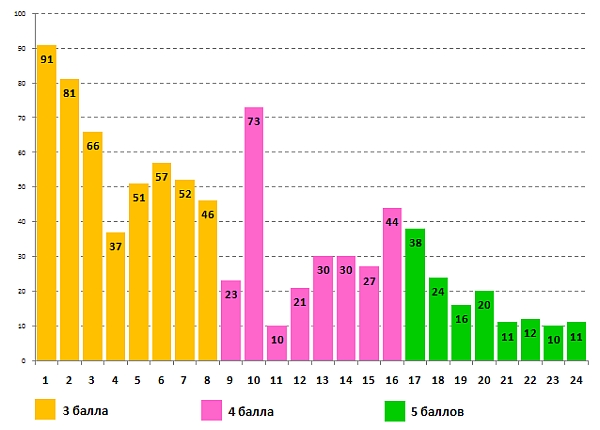
Проценты участников, правильно решивших задачи задания для 5-6-х классов:
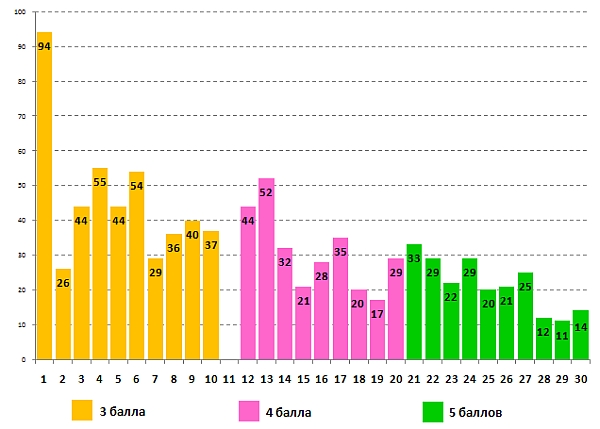
В этом задании из-за технической ошибки в задаче №11 задания на белорусском языке отсутствовал правильный рисунок-иллюстрация. Из-за неправильного изображения к заданию в белорусском переводе, чтобы всех участников поставить в одинаковые условия, эта задача не оценивалась.
Диаграмма по 7-8-м классам:
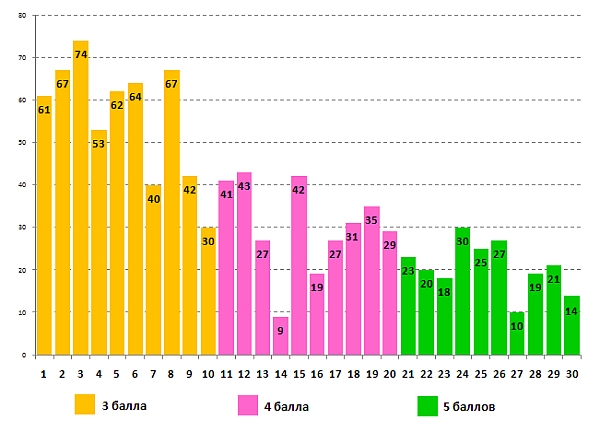
Данные о выполнении задания участниками – учащимися 9-10-х классов:
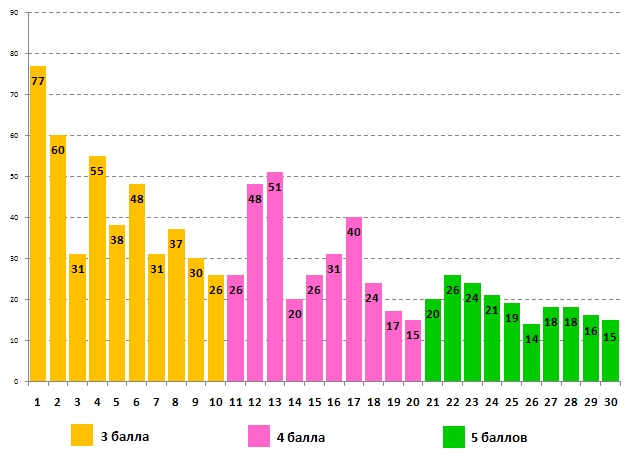
Информация об успешности выполнения задания учащимися 11 класса:
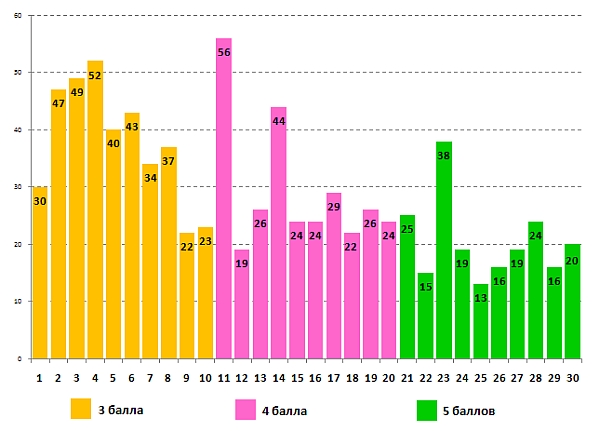
Следующая диаграмма характеризует уровень сложности заданий в целом. На ней представлены средние баллы участников для каждой параллели:
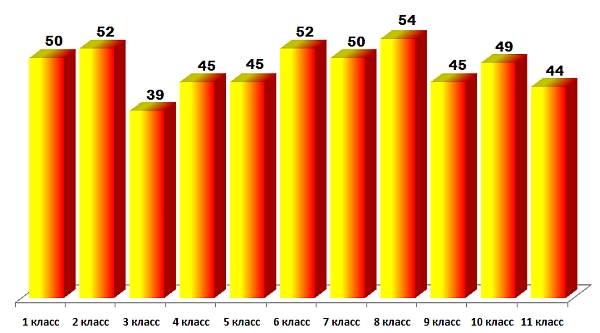
Эти диаграммы наглядно демонстрируют, что в отведённое время выполнить задание полностью, решив правильно все задачи, под силу далеко не каждому. Объём и содержание задания не предполагают его полного выполнения. Организаторы конкурса «Кенгуру» и авторы заданий надеются, что участники заинтересуются оригинальными, сложными и интересными задачами и после игры-конкурса продолжат поиск решения самостоятельно или с помощью учителя, родителей, совместно с друзьями. «Математика существует не для того, чтобы навязывать кому-либо тяжелую работу. Наоборот, она существует только для удовольствия. Для удовольствия тех, кто любит анализировать то, что он делает, или может сделать, или то, что уже сделал в надежде сделать это еще лучше» (Роберт Брингхерст, канадский поэт, типограф, литератор).
Посмотреть ответы участника на каждую задачу задания, правильные варианты ответов, промежуточные и окончательный результаты можно, воспользовавшись ссылкой в поле с фамилией и именем учащегося в итоговой таблице результатов (подробнее см. статью Как посмотреть результаты участия в конкурсе).
Обращаем внимание всех участников, родителей и учителей, что самостоятельная и честная работа над заданием – главное требование к организаторам и участникам конкурса. Оргкомитет сожалеет, что по итогам работы дисквалификационной комиссии обнаружены случаи нарушения правил игры-конкурса в отдельных учреждениях образования и отдельными участниками. Игра-конкурс "Кенгуру" проводится с целью развития и поддержки интереса школьников к изучению математики. А «математику нельзя изучать, наблюдая, как это делает сосед!» (Айвен Нивен, канадско-американский математик, специалист в теории чисел), «…если хотите научиться решать задачи, то решайте их!» (Дьёрдь Пойа, венгерский, швейцарский и американский математик).
Оргкомитет поздравляет всех участников игры-конкурса "Кенгуру-2015". Каждый участник получит приз «для всех». Учащиеся, показавшие лучшие результаты, будут поощрены дополнительными призами. Часто увлечение математикой начинается с решения какой-либо понравившейся нестандартной задачи. Мы надеемся, что каждый участник нашёл для себя интересные, занимательные, развивающие нестандартное мышление задачи.
Выражаем благодарность организаторам-координаторам игры-конкурса в районах (городах) и в учреждениях образования, которые ответственно отнеслись к организации и проведению конкурса, поддерживают и развивают интерес своих учеников к математике, помогают им поверить в силы и возможности, учат радоваться своим, пусть даже пока не очень большим, успехам.
Всем участникам конкурса желаем хороших впечатлений от игры. Успехов в изучении математики!



