Результаты конкурса "Кенгуру-2016"

Подведены итоги конкурса "Кенгуру-2016". Международная математическая игра-конкурс "Кенгуру-2016" проводилась 17 марта 2016 года. 136 832 учащихся из 2 754 учреждений образования Республики Беларусь приняли участие в самом массовом математическом соревновании школьников в мире.

Математика — одна из самых древних наук, которая постоянно развивается и эволюционирует, оказывая влияние на нашу повседневную жизнь. А.Д. Александров, математик, физик и философ сказал: «Ничего нельзя сделать без математики: мост построить нельзя, плотину – нельзя, гидростанцию – нельзя. Сокращать объём преподавания математики – преступление! Надо изучать её как можно в большем объёме, а главное – как можно основательнее». Математика есть во всем, что нас окружает, благодаря математике мы имеем все доступные нам сегодня технологии. Эта наука является одним из самых важных достижений цивилизации. Без нее развитие технологий и познание природы были бы немыслимы! Особенно математика важна для формирования личности школьников, она дает огромный толчок для умственного развития и рационального мышления на всю жизнь вперед.

Математики во всём мире прилагают усилия для популяризации этой дисциплины среди школьников, стремятся показать, что математика не так скучна, как она представляется некоторым учащимся на уроках при изучении тем из школьной программы. С целью развития и поддержки интереса школьников к изучению этого предмета во многих странах ежегодно, в каждый третий четверг марта месяца, проводится международная математическая игра-конкурс «Кенгуру». Задания этой игры подобраны так, что каждый её участник видит, где в жизни могут конкретно пригодиться знания математики, а самый «неисправимый гуманитарий» может найти в них интересную для себя задачу.

В международную ассоциацию «Кенгуру без границ» (KSF — Le Kangourou sans Frontieres) сегодня входит 59 стран. Девиз ассоциации — «Математика для всех!».

17 марта ребята из разных стран пробовали свои силы в решении оригинальных математических задач, которые готовятся лучшими учителями и преподавателями и утверждаются на ежегодной конференции стран-участниц KSF. В нашей стране в этот день задачи решали 136 832 учащихся, что на 9308 больше по сравнению с предыдущим конкурсом. Увеличение количества участников произошло по всем регионам. Наибольшее количество учащихся, участников этого интеллектуального соревнования, зарегистрировано в столице. Количество участников по регионам отражено на диаграмме:

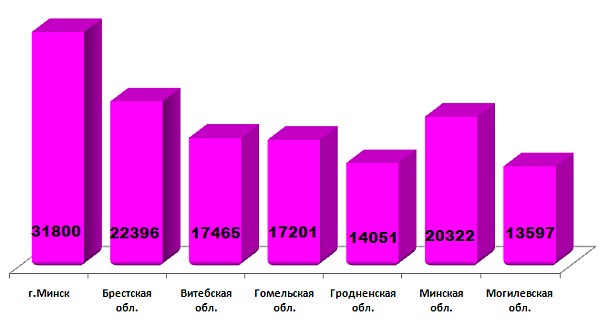
Задания «Кенгуру» разрабатываются для шести возрастных групп: для 1-2, 3-4, 5-6, 7-8, 9-10 и 11 классов. Распределение участников в соответствии с классами следующее:

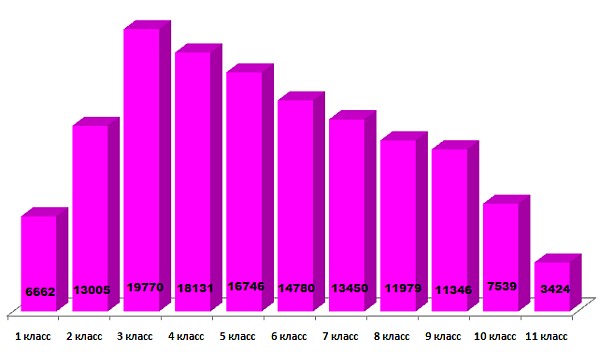
Напомним, что по правилам конкурса все задачи в задании условно разбиты на три уровня сложности: простые и занимательные вопросы, каждый из которых оценивается в 3 балла; более сложные задачи, для решения которых иногда требуется хорошее знание школьной программы по математике (оцениваются в 4 балла); сложные, нестандартные задачи, для решения которых надо проявить смекалку, умение рассуждать, анализировать (оцениваются в 5 баллов). Успешность выполнения заданий отражена на следующих диаграммах.

Информация об успешности выполнения задания для 1-2-х классов, над которым трудились самые юные участники:

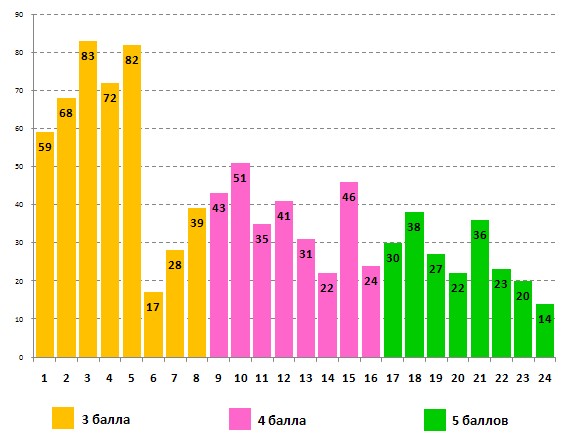
Успешность выполнения этого же задания учащимися 2-х классов:

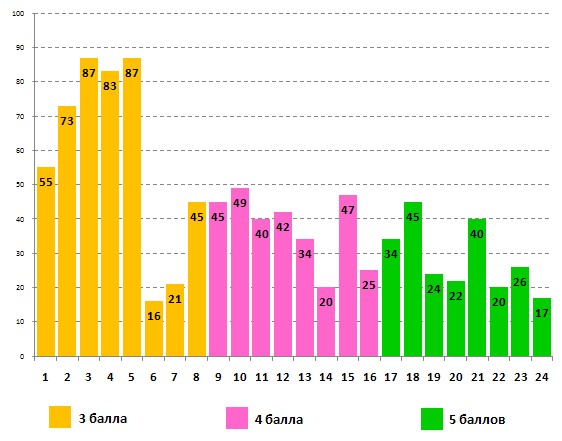
При анализе результатов этого задания удивление вызывает низкий процент правильных ответов участников на решение задач №6 и №7, относящихся к простым, трехбалльным вопросам. Объяснить это можно невнимательностью ребят: в задаче №6 участники забыли посчитать самого именинника, а в задаче №7 – дома, с которых начинается или заканчивается доставка телеграмм. Удивительно также, что с некоторыми задачами, в том числе и с упомянутыми выше, первоклассники справились более успешно, чем второклассники. Это задачи задания №1, №6, №7, №10, №14, №19 и №22. Этот факт наводит на некоторые размышления, и у оргкомитета конкурса есть на этот счёт свои соображения, которые они могут высказать только конкретным учреждениям и конкретным организаторам в этих учреждениях.

Процент правильно решённых задач задания для 3-4-х классов третьеклассниками:

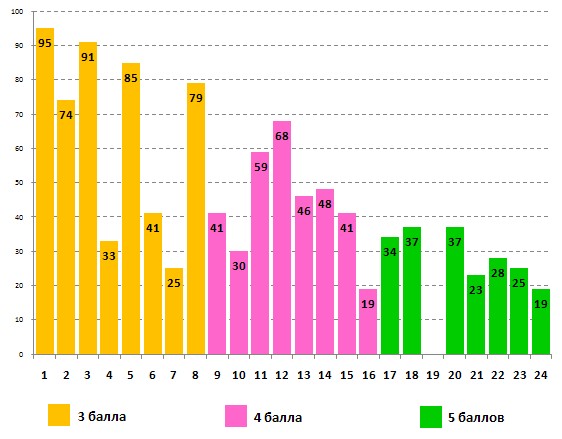
Успешность выполнения этого же задания учащимися 4-х классов:

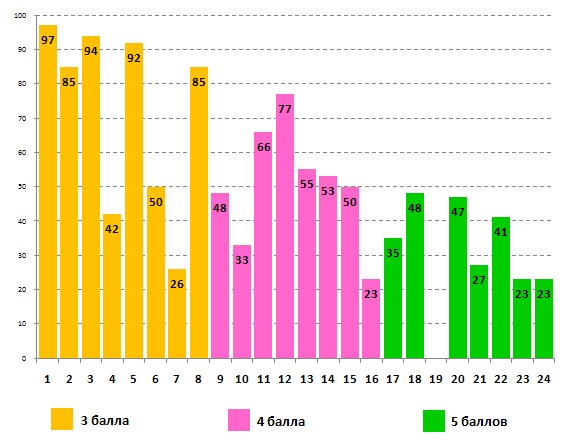
В этом задании задача №19 не оценивалась из-за наличия двух правильных вариантов ответа.

В этом задании, как и в задании для 1-2 классов, оказалась «лёгкая» задача, на которую правильных ответов участниками дано меньше, чем ожидалось. При ответе на вопрос №7 большая часть ребят выбрали вариант ответа «квадрат», видимо, не обратив внимания, на формулировку вопроса («часть чёрного квадрата, которая накрыта серым прямоугольником»). В процентном отношении по количеству правильно решённых задач четвероклассники подтвердили более высокий уровень знаний по сравнению с третьеклассниками. Со всеми задачами, за исключением задачи №23, старшие ребята справились более успешно.

Статистические данные о выполнении задания для 5-6-х классов учащимися 5-х классов:

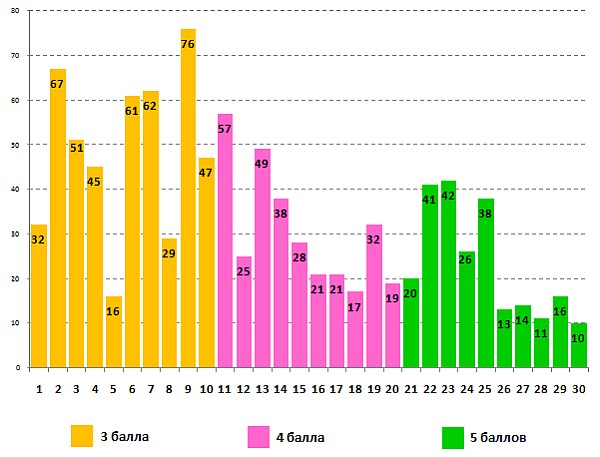
Успешность выполнения этого же задания учащимися 6-х классов:

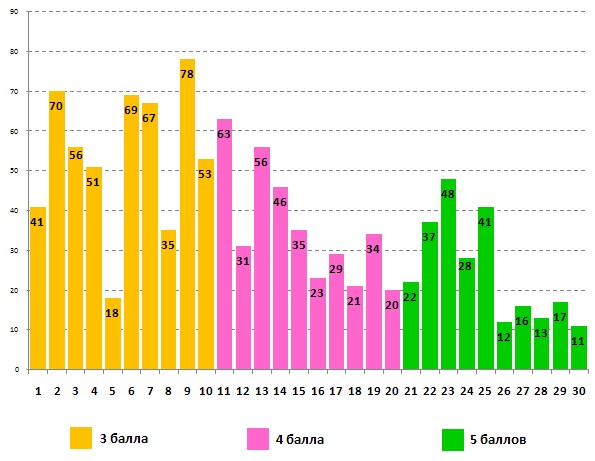
В этом задании также оказался «простой», в три балла, вопрос, удивляющий количеством неправильных ответов, – это задача №5. Только 16% пятиклассников и 18% шестиклассников правильно определили, что площадь маленького квадрата равна половине площади большого. Решая одни и те же задачи с пятиклассниками, шестиклассники подтвердили, что приобрели больше знаний, успешнее справившись с заданием. Только на задачи №22 и №26 процент правильных ответов у пятиклассников выше, чем у шестиклассников.

Данные об успешности выполнения задания для 7-8-х классов учащимися 7-х классов:

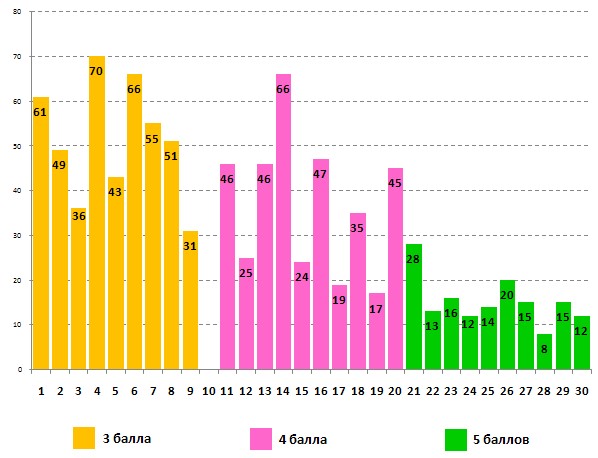
Данные о выполнении этого же задания участниками – учащимися 8-х классов:

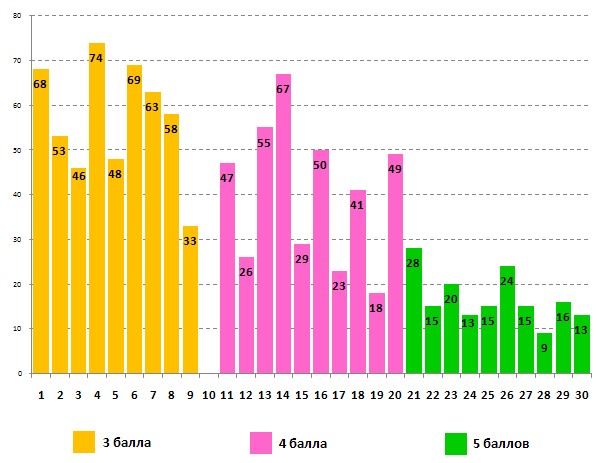
В этом задании из-за технической ошибки в задаче №10 задания на русском языке отсутствовал рисунок-иллюстрация. По этой причине эта задача не оценивалась. Сравнительный анализ успешности выполнения задания свидетельствует, что процент правильно решённых задач выше у старших ребят, только с задачами №14, №29 и №30 семиклассники справились немного успешнее.

Информация об успешности выполнения задания для 9-10-х классов, над которым трудились девятиклассники:

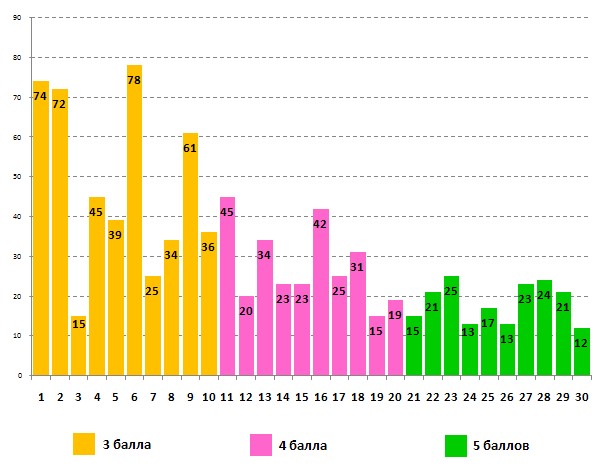
Успешность выполнения этого же задания учащимися 10-х классов:

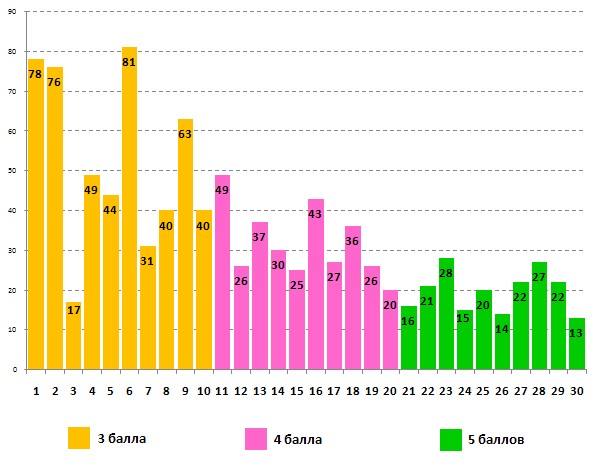
Десятиклассники не позволили девятиклассникам «обогнать» себя по результатам работы над заданием. Однако и те и другие «оплошали» при решении задачи №3, которая разработчиками отнесена к лёгким трёхбалльным вопросам.

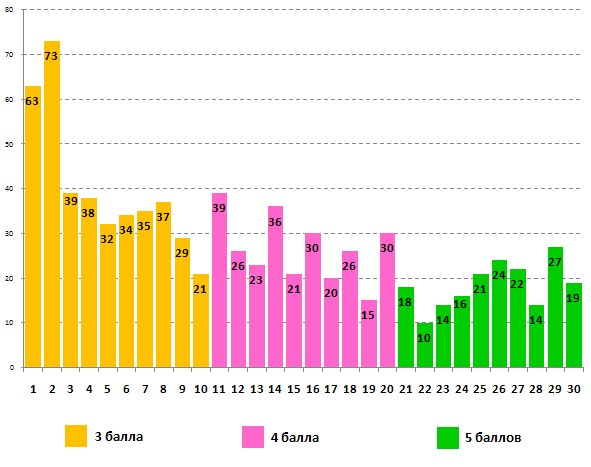
Информация об успешности выполнения задания учащимися 11 класса:

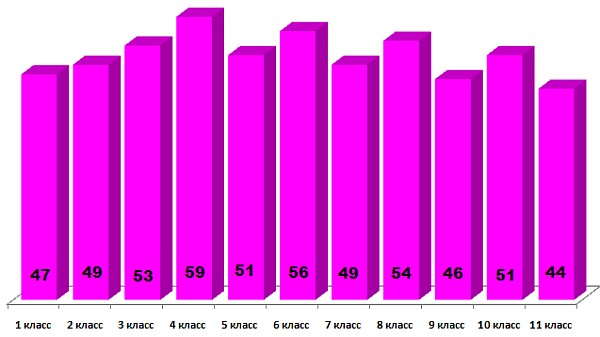
Следующая диаграмма характеризует уровень сложности заданий в целом. Она знакомит со средними баллами по стране для каждой параллели:

Напоминаем, что просмотреть ответы участника на каждую задачу задания, правильные варианты ответов, промежуточные и окончательный результаты можно, воспользовавшись ссылкой в поле с фамилией и именем учащегося в итоговой таблице результатов.

Обращаем внимание всех участников, родителей и учителей, что самостоятельная и честная работа над заданием – главное требование к организаторам и участникам конкурса. Оргкомитет сожалеет, что по итогам работы дисквалификационной комиссии обнаружены случаи нарушения правил игры-конкурса в отдельных учреждениях образования и отдельными участниками. Как всегда такими нарушениями в основном страдает начальная школа, где некоторые учителя путают понятия «помощь» и «медвежья услуга».

Оргкомитет поздравляет всех участников игры-конкурса "Кенгуру-2016". Каждый участник получит приз «для всех». Учащиеся, показавшие лучшие результаты, будут поощрены дополнительными призами. Выражаем благодарность организаторам-координаторам игры-конкурса в районах (городах) и в учреждениях образования, которые ответственно отнеслись к организации и проведению конкурса.

Всем участникам конкурса желаем хороших впечатлений от игры. Успехов в изучении математики!