1
Каждый год третий четверг марта называют Днём Кенгуру. Дата одного из следующих Дней Кенгуру указана неправильно. Какая именно?
A) 17 марта 2022 г.
Б) 16 марта 2023 г.
В) 14 марта 2024 г.
Г) 20 марта 2025 г.
Д) 19 марта 2026 г.
2
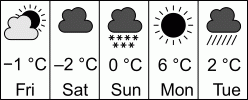
Женя каждый день просматривает приложение, которое показывает прогнозируемую погоду и максимальную температуру на ближайшие пять дней. В каком из следующих ответов приведён график максимальной температуры данного на рисунке прогноза?

3
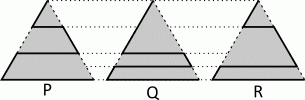
Парк имеет форму равностороннего треугольника. Кошка хочет пройти от верхней вершины до правой нижней вершины по одному из трёх путей, выделенных жирной линией. Длины путей обозначены буквами P, Q и R, как показано на рисунке. Какое из следующих соотношений является верным?
A) P < Q < R
Б) P < R < Q
В) P < Q = R
Г) P = R < Q
Д) P = Q = R
4
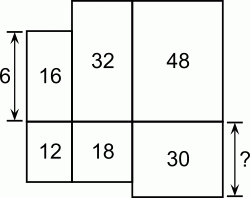
Шесть прямоугольников расположены так, как показано на рисунке. Левый верхний прямоугольник имеет высоту 6 см. Числа внутри прямоугольников указывают их площадь в см2. Какую высоту имеет правый нижний прямоугольник?
A) 4 см Б) 5 см В) 6 см Г) 7,5 см Д) 10 см
5
Первый тайм гандбольного матча закончился со счётом 9 : 14, т. е., команда гостей опережала команду хозяев на 5 мячей. Но во втором тайме хозяева забили вдвое больше голов, чем их соперники, и в результате выиграли матч с перевесом в 1 мяч. С каким счётом закончился матч?
A) 20 : 19
Б) 21 : 20
В) 22 : 21
Г) 23 : 22
Д) 24 : 23
6
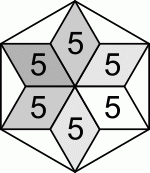
Шесть равных ромбов, каждый площадью 5 см2, образуют звезду. Концы звезды соединили отрезками, и в результате получился правильный шестиугольник, показанный на рисунке. Какую площадь он имеет?
A) 36 см2
Б) 40 см2
В) 45 см2
Г) 48 см2
Д) 60 см2
7
В джаз-бэнде Джузеппе играет на саксофоне, Серджио – на трубе, а Элиана поёт. Все они одного возраста. В состав джаз-бэнда входят ещё трое участников, их возрасты: 19, 20 и 21 год. Средний возраст всех участников джаз-бэнда равен 21 году. Сколько лет Элиане?
A) 20 Б) 21 В) 22 Г) 23 Д) 24
8
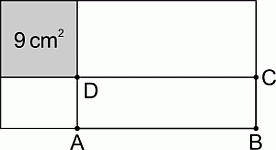
Прямоугольник с периметром 30 см разбит на 4 прямоугольника, как показано на рисунке. Один из них – квадрат площадью 9 см2. Чему равен периметр прямоугольника ABCD?
A) 14 см Б) 16 см В) 18 см Г) 21 см Д) 24 см
9
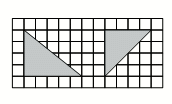
Алла нарисовала на клетчатой бумаге три треугольника. Ровно два из них имеют одинаковую площадь, ровно два из них равнобедренные, и ровно два – прямоугольные. На рисунке показаны два из этих треугольников. Каким может быть третий?

10
Кенгурёнок обнаружил любопытное число: если вычесть из него 1/10, то получится такой же результат, как и при умножении этого числа на 1/10. Какое число обнаружил кенгурёнок?
A) 1/100 Б) 1/11 В) 1/10 Г) 11/100 Д) 1/9
11
У Тома было десять бенгальских огней одинакового размера. Он зажёг первый из них. Когда до его сгорания оставалась десятая часть, он зажёг второй. Когда до сгорания оставалась десятая часть второго огня, он зажёг третий огонь и т.д. Бенгальские огни горят с одинаковой скоростью по всей длине. Один бенгальский огонь сгорает за 2 минуты. За какое время сгорели все 10 огней?
A) 18 мин 20 сек
Б) 18 мин 12 сек
В) 18 мин
Г) 17 мин
Д) 16 мин 40 сек
12
Миша хочет подняться по лестнице на 8 ступенек. За один шаг он может подняться на 1 или 2 ступеньки. Но шестая ступенька сломана, поэтому он не может стать на неё. Сколько всего имеется различных способов, чтобы Миша мог дойти до 8-й ступеньки, став на неё?
A) 6 Б) 7 В) 8 Г) 9 Д) 10
13
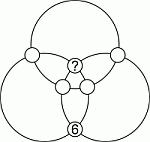
В кружочки на пересечениях трёх колец вписаны числа от 1 до 6. На рисунке указано положение числа 6. Суммы чисел, записанных во всех четырёх кружочках каждого кольца, одинаковы. Какое число находится в кружочке со знаком вопроса?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
14
Число 2021 при делении на 6, 7, 8 и 9 даёт один и тот же остаток 5. Сколько всего натуральных чисел, меньших 2021, тоже дают остаток 5 при делении на 6, 7, 8 и 9?
A) 4 Б) 3 В) 2 Г) 1 Д) ни одного
15
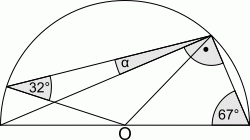
На рисунке показан полукруг с центром O и указаны величины двух углов. Какова величина угла α?
A) 9° Б) 11° В) 16° Г) 17,5° Д) 18°
16
Имеется пять коробок, в каждой из которых лежат шары. Количества шаров в коробках соответственно равны: 9, 15, 17, 19 и 21. В каждой коробке либо все шары красные, либо все шары синие. Когда убрали одну из коробок, то в оставшихся четырёх коробках число красных шаров стало ровно в 3 раза больше числа синих. Сколько шаров было в убранной коробке?
A) 9 Б) 15 В) 17 Г) 19 Д) 21
17
Пять автомобилей стартовали в следующем порядке:

Каждый раз, когда одна машина обгоняла другую, ей начислялось 1 очко. Машины финишировали в следующем порядке:

Каково наименьшее возможное общее количество всех начисленных очков?
A) 10 Б) 9 В) 8 Г) 7 Д) 6
18

В каждой клетке квадрата 3 × 3 было записано число 0. За один ход можно увеличить на 1 числа во всех клетках какого-то из четырёх квадратов 2 × 2, содержащихся в квадрате 3 × 3 (например, в клетках серого квадрата на первом рисунке). После нескольких ходов получился квадрат, показанный на втором рисунке. Но некоторые числа в этом квадрате скрыты. Какое число может быть в клетке со знаком вопроса?
A) 14 Б) 15 В) 16 Г) 17 Д) 19
19
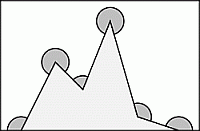
Чему равна сумма отмеченных на рисунке углов?
A) 360° Б) 900° В) 1080° Г) 1120° Д) 1440°
20
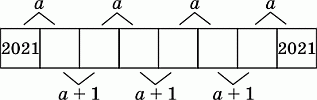
Полоска состоит из 8 клеток. Суммы чисел в парах соседних клеток равны a или a + 1, как показано на рисунке. Числа в крайних клетках равны 2021. Чему равно a?
A) 4041 Б) 4042 В) 4043 Г) 4044 Д) 4045
21
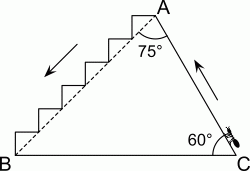
Муравей поднимается по наклонной тропинке CA и спускается по лестнице от A к B, как показано на рисунке. Чему равно отношение пути от С до A к пути от A до В?
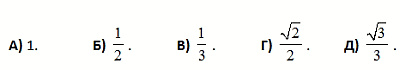
22
Числа a, b и c удовлетворяют равенствам a + b + c = 0 и abc = 78. Чему может быть равно выражение
(a + b) (b + c) (c + a)?
A) –156
Б) –39
В) 78
Г) 156
Д) ни одному из предыдущих
23
Пусть N – наименьшее натуральное число, сумма цифр которого равна 2021. Чему равна сумма цифр числа N + 2021?
A) 10 Б) 12 В) 19 Г) 28 Д) 2021
24
Трое мальчиков играют в игру «Слова», в которой они пишут по 10 слов. Каждый игрок получает 3 балла за каждое слово, которого нет у других игроков, а за каждое слово, которое встречается только у одного из двух других игроков, он получает 1 балл. За слова, которые встречаются у всех трёх игроков, баллов не начисляется. После игры мальчики подсчитали свои баллы, и оказалось, что у всех результаты разные. У Сени оказалось меньше всего – 19 баллов. Больше всего баллов оказалось у Димы. Сколько баллов набрал Дима?
A) 20 Б) 21 В) 23 Г) 24 Д) 25
25
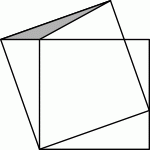
На рисунке площадь меньшего квадрата равна 16, а площадь серого треугольника равна 1. Чему равна площадь большего квадрата?
A) 17 Б) 18 В) 19 Г) 20 Д) 21
26
Числа a и b являются квадратами целых чисел. Разность a – b является простым числом. Какое из следующих значений может принимать b?
A) 100 Б) 144 В) 256 Г) 900 Д) 10000
27
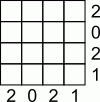
В таблице 4 × 4 некоторые клетки нужно окрасить в чёрный цвет. Числа, записанные справа от строчек и ниже столбцов, указывают, сколько чёрных клеток должно быть в соответствующей строчке или столбце. Сколько всего существует различных раскрасок, удовлетворяющих этим условиям?
A) 1 Б) 2 В) 3 Г) 5 Д) больше 5
28
У скольких пятизначных натуральных чисел произведение цифр равно 1000?
A) 10 Б) 20 В) 30 Г) 40 Д) 60
29
У Кристины есть восемь монет, веса которых выражаются разными натуральными числами граммов. Как бы Кристина ни положила по две монеты на две чаши весов, всегда перевесит та чаша, на которой находится самая тяжёлая из четырёх монет на весах. Какой наименьший вес может быть у самой тяжёлой монеты?
A) 8 г Б) 12 г В) 34 г Г) 128 г Д) 256 г
30
2021 мяч выложены в ряд и пронумерованы числами от 1 до 2021. Каждый мяч окрашен в один из четырёх цветов: зелёный, красный, жёлтый или синий. Известно, что одновременно выполнены следующие три условия:
1) среди любых пяти подряд лежащих мячей есть ровно один красный, один жёлтый и один синий мяч;
2) после каждого красного мяча лежит жёлтый мяч;
3) мячи с номерами 2, 20 и 202 зелёные.
Какого цвета мяч номер 2021?
A) зелёный
Б) красный
В) жёлтый
Г) синий
Д) невозможно определить