1
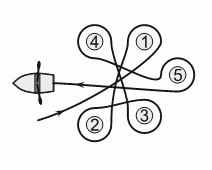
Миша проплыл на лодке вокруг пяти буёв, как показано на рисунке. Какие буи он огибал по ходу часовой стрелки?
A) 2, 3 и 4
Б) 1, 2 и 3
В) 1, 3 и 5
Г) 2, 4 и 5
Д) 2, 3 и 5
2
Света хочет сложить в некотором порядке следующие 5 карточек с числами так, чтобы у неё получилось наименьшее возможное 9-значное число. Какую карточку ей нужно положить на краю справа?

3
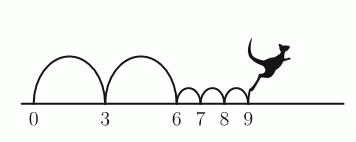
Кенгуру прыгает вдоль числовой прямой, начав с числа 0. Он чередует длинные и короткие прыжки. После двух длинных прыжков он делает три короткие, затем – снова два длинные, три короткие и т.д. На какое из следующих чисел выпадет прыжок кенгуру?
A) 82 Б) 83 В) 84 Г) 85 Д) 86
4
У автомобиля Кенгуру отвалился номер. Кунгуру прикрепил его на место, но перепутал верх и низ. Однако, номер стал читаться так же, как и раньше. Каким из следующих мог быть номер автомобиля Кенгуру?

5
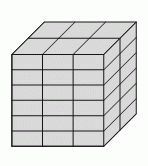
У Роба Билдера есть кирпичи. Меньшая их сторона равна 4 см. Роб сложил из таких кирпичей куб так, как показано на рисунке. Какие размеры (в см) имеют кирпичи?
A) 4 × 6 × 12
Б) 4 × 6 × 16
В) 4 × 8 × 12
Г) 4 × 8 × 16
Д) 4 × 12 × 16
6
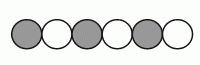
Черно-белая гусеница (см. рис.) свернулась калачиком. Как теперь она может выглядеть?
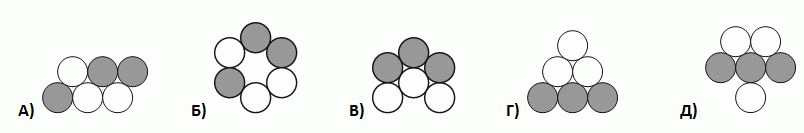
7

В следующем выражении 5 пустых клеток. Саня хочет вписать в них четыре знака плюс и один знак минус так, чтобы получилось правильное равенство. В какую клетку ей следует вписать знак минус?
A) между 6 и 9
Б) между 9 и 12
В) между 12 и 15
Г) между 15 и 18
Д) между 18 и 21
8
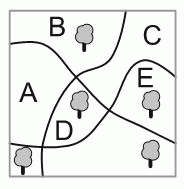
В парке растут 5 деревьев и имеется 3 дорожки (см. рис.). В какой части парка следует посадить ещё одно дерево, чтобы у каждой дорожки с обеих сторон было одинаковое количество деревьев?
A) A Б) B В) C Г) D Д) E
9
Сколько чисел от 100 до 300 состоят только из нечётных цифр?
A) 25 Б) 50 В) 75 Г) 100 Д) 150
10

Жора вычислил сумму квадратов двух чисел. К сожалению, на бумагу пролились чернила и некоторые цифры оказались скрыты. Какой цифрой заканчивается первое число?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
11
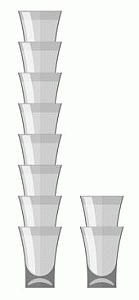
Расстояние между двумя полками в кухонном шкафу Моники составляет 36 см. Она знает, что стопка из 8 её стаканов имеет высоту 42 см, а стопка из 2 стаканов – 18 см (см. рис.). Какое наибольшее число стаканов Моника может собрать в стопку, чтобы её можно было поставить на полку в шкафу?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
12
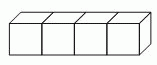
У стандартного игрального кубика количество точек на противоположных гранях равно 7. Четыре стандартных кубика склеили так, как показано на рисунке. Какое наименьшее количество точек может быть на поверхности полученной фигуры?
A) 52 Б) 54 В) 56 Г) 58 Д) 60
13
Средний возраст трёх сестёр составляет 10 лет. Если считать их возраст парами, то в двух из пар средний возраст равен 11 и 12 лет. Сколько лет старшей из сестёр?
A) 10 Б) 11 В) 12 Г) 14 Д) 16
14
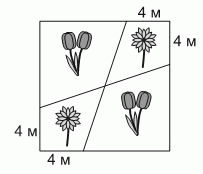
Садовник Тони посадил тюльпаны  и ромашки
и ромашки  на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?
на квадратной клумбе со стороной 12 м, как показано на рисунке. Чему равна площадь двух частей клумбы, на которых он посадил ромашки?
A) 48 м2 Б) 46 м2 В) 44 м2 Г) 40 м2 Д) 36 м2
15
В моём кабинете двое настенных часов. Одни спешат на 1 минуту в час, а другие на 2 минуты в час отстают. Вчера я установил правильное время на обоих часах. Но сегодня, когда я посмотрел на часы, то обнаружил, что одни часы показывают 11:00, а другие 12:00. Когда вчера я установил время на часах?
A) 23:00 Б) 19:40 В) 15:40 Г) 14:00 Д) 11:20
16
Ваня записал на доске несколько натуральных чисел, меньших 7. Рита стёрла все эти числа и каждое число Вани заменила числом, которое получится, если от 7 отнять число Вани. Сумма чисел, записанных Ваней, равнялась 22, сумма чисел, записанных Ритой, оказалась равна 34. Сколько чисел записал на доске Ваня?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
17
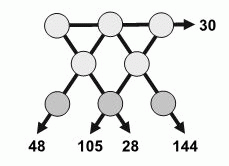
Числа от 1 до 8 вписаны в кружочки на рисунке (каждое ровно один раз). Произведения троек чисел, расположенных на одной прямой, указаны на данном рисунке. Чему равна сумма трёх чисел в нижнем ряду?
A) 11 Б) 12 В) 15 Г) 17 Д) 19
18
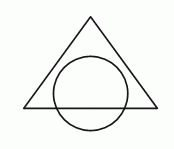
Площадь пересечения круга и треугольника составляет 45% от площади их объединения. Площадь части треугольника вне круга составляет 40% от площади их объединения. Сколько (по площади) процентов круга лежит за пределами треугольника?
A) 20% Б) 25% В) 30% Г) 35% Д) 50%
19
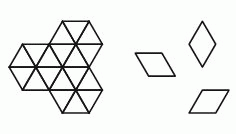
Сколько существует различных способов замощения следующей фигуры указанными на рисунке ромбиками?
A) 1 Б) 6 В) 8 Г) 9 Д) 12
20
Марк всегда ездит на велосипеде с одной и той же скоростью и ходит с одной и той же скоростью. На расстояние от дома до школы и обратно на велосипеде ему нужно 20 минут, а на такое же расстояние пешком ─ 60 минут. Вчера Марк поехал в школу на велосипеде, но оставил его у дома Евы и дальше пошёл пешком. На обратном пути он дошел до дома Евы и дальше поехал на велосипеде. На этот раз на всю дорогу от дома до школы и обратно Марку понадобилось 52 минуты. Какую часть пути Марк ехал на велосипеде?
A) 1/6 Б) 1/5 В) 1/4 Г) 1/3 Д) 1/2
21

Аня решила вписать числа в клетки таблицы 3 × 3 так, чтобы суммы чисел во всех квадратах 2 × 2 были одинаковыми. Три числа она уже вписала так, как показано на рисунке. Какое число должно быть вписано в клетку, отмеченную знаком вопроса?
A) 0 Б) 1 В) 4 Г) 5 Д) 6
22
Деревни A, B, C и D расположены (в каком-то порядке) вдоль длинной прямой дороги. Расстояние между A и C равно 75 км, расстояние между B и D – 45 км, а между B и C – 20 км. Каким из следующих НЕ МОЖЕТ быть расстояние между A и D?
A) 10 км Б) 50 км В) 80 км Г) 100 км Д) 140 км
23
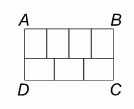
Прямоугольник ABCD состоит из семи меньших равных прямоугольников (см. рис.). Чему равно отношение AB : BC?
A) 1/2 Б) 3/4 В) 8/5 Г) 12/7 Д) 7/3
24
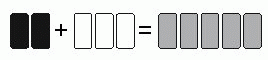
Художник хотел смешать 2 литра чёрной краски с 3 литрами белой краски, чтобы получилось 5 литров серой краски. Однако, по ошибке он смешал 3 литра чёрной с 2 литрами белой. В результате получился неправильный оттенок серого цвета. Какое наименьшее количество этой серой краски нужно отлить, чтобы в остаток этой краски можно было добавить некоторое количество белой краски и получить 5 литров серой краски нужного оттенка?
A) 5/3 литра Б) 3/2 литра В) 2/3 литра Г) 3/5 литра Д) 5/9 литра
25
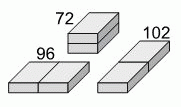
У строителя есть два одинаковых кирпича. Если сложить их тремя разными способами, как показано на рисунке, то получатся блоки, площади поверхности которых равны 72 см2, 96 см2 и 102 см2. Чему равна площадь поверхности одного такого кирпича?
A) 36 см2 Б) 48 см2 В) 52 см2 Г) 54 см2 Д) 60 см2
26

Какое наименьшее количество клеток нужно окрасить в квадрате 5 × 5, чтобы в любом прямоугольнике 1 × 4 и 4 × 1, состоящем из четырёх клеток, была хотя бы одна окрашенная клетка?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
27
Маугли спрашивает зебру и пантеру, какой сегодня день. Зебра всегда врёт в понедельник, вторник и среду. Пантера всегда врёт в четверг, пятницу и субботу. Зебра говорит: «Вчера был один из дней, когда я вру». Пантера говорит: «Вчера тоже был один из дней, когда я вру». Какой сегодня день?
A) четверг Б) пятница В) суббота Г) воскресенье Д) понедельник
28
На прямой было отмечено несколько точек. Роман между любыми двумя соседними отмеченными точками отметил ещё по одной точки. Затем он повторил эту процедуру ещё 3 раза. В результате получилось 225 отмеченных точек. Сколько отмеченных точек было вначале?
A) 10 Б) 12 В) 15 Г) 16 Д) 25
29
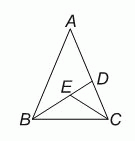
Равнобедренный треугольник АВС (АВ = АС) разрезали на три меньших равнобедренных треугольника, как показано на рисунке. При этом AD = DB, CE = CD = ВE. Найдите величину угла BAC.
A) 24° Б) 28° В) 30° Г) 35° Д) 36°
30
В семи парках обитает 2022 кенгуру и несколько коал. В каждом парке количество кенгуру равно общему количеству коал во всех остальных парках. Сколько всего коал обитает во всех семи парках?
A) 288 Б) 337 В) 576 Г) 674 Д) 2022