1
Какой из следующих знаков зодиака имеет ось симметрии?
A)  стрелец
стрелец
Б)  скорпион
скорпион
В)  лев
лев
Г)  рак
рак
Д)  козерог
козерог
2
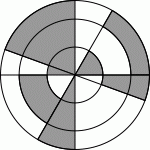
На рисунке показаны три концентрических круга с четырьмя отрезками, проходящими через их общий центр. Сколько процентов площади большего круга закрашены?
A) 30% Б) 35% В) 40% Г) 45% Д) 50%
3
Чему равно значение выражения 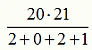 ?
?
A) 42 Б) 64 В) 80 Г) 84 Д) 105
4
Сколько существует четырёхзначных чисел, цифры которых – последовательные натуральные числа, записанные в порядке возрастания слева направо?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
5

Если правильно сложить 5 плиток пазла, получится прямоугольник с примером на вычитание. Чему равен результат вычислений в этом примере?
A) –100 Б) -8 В) -1 Г) 199 Д) 208
6
Каждая из пяти следующих ваз имеет одинаковую высоту и объем в 1 литр. В каждую вазу налили по поллитра воды. В какой вазе уровень воды самый высокий?
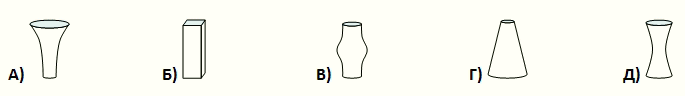
7
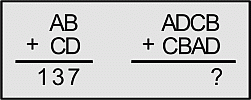
Школьник правильно сложил два двузначных числа в левой части доски и получил 137. Какой результат получится, если правильно сложить четырёхзначные числа в правой части доски?
A) 13737 Б) 13837 В) 14747 Г) 23737 Д) 137137
8
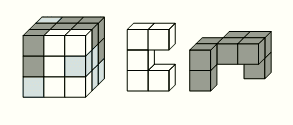
Куб 3 × 3 × 3 состоит из единичных кубиков чёрного, белого и серого цвета (см. рис.) Справа показаны фигуры, которые образуют все белые кубики и все чёрные кубики. Какую фигуру образуют все серые кубики?

9
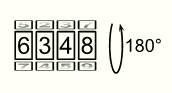
Велосипедный замок состоит из четырёх колец, на которых записаны в порядке возрастания цифры от 0 до 9. Чтобы получить правильный код, нужно каждое кольцо повернуть на 180° (см. рис.) Какой код замка правильный?
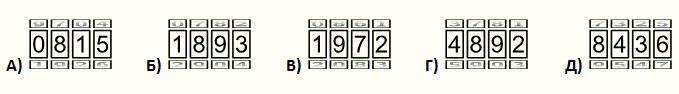
10
Боря на 5 см выше Ани, но на 10 см ниже Васи. Гена на 10 см выше Васи, но на 5 см ниже Димы. Какое из следующих утверждений верно?
A) Аня и Дима одного роста.
Б) Аня на 10 см выше Димы.
В) Аня на 10 см ниже Димы.
Г) Аня на 30 см выше Димы.
Д) Аня на 30 см ниже Димы.
11
Прямоугольная плитка шоколада состоит из квадратных долек. Коля отломал две полные полоски и съел полученные 12 долек. Затем Дима отломал от оставшейся части одну целую полоску и съел 9 полученных долек. Сколько долек шоколада осталось в плитке?
A) 72 Б) 63 В) 54 Г) 45 Д) 36
12
Банка, наполненная водой на одну пятую, весит 560 г. Та же банка, наполненная водой на четыре пятых, весит 740 г. Сколько весит пустая банка?
A) 60 г Б) 112 г В) 180 г Г) 300 г Д) 500 г
13
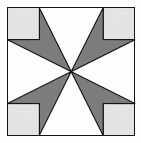
Площадь большого квадрата на рисунке равна 16 см2, а площадь каждого маленького серого квадрата – 1 см2. Чему равна площадь тёмного цветка?
A) 3 см2
Б) 3,5 см2
В) 4 см2
Г) 5,5 см2
Д) 6 см2
14
Костя построил новый забор в своём саду. Ему понадобилось 25 деревянных досок, каждая из которых имеет длину 30 дм. Он прибил эти доски с небольшими одинаковыми перекрытиями соседних досок, как показано на рисунке. Общая длина нового забора Кости составила 69 метров. Какова длина одного перекрытия?

A) 2,4 дм Б) 2,5 дм В) 3 дм Г) 4,8 дм Д) 5 дм
15
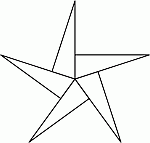
Пять одинаковых прямоугольных треугольников расположены так, что они, соприкасаясь бóльшими острыми углами, образуют звезду. Сколько всего потребуется таких треугольников, чтобы аналогично построить звезду, у которой соприкасаются меньшие острые углы?
A) 10 Б) 12 В) 18 Г) 20 Д) 24
16
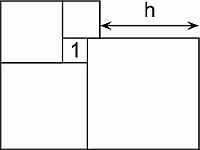
Пять квадратов расположены так, как показано на рисунке. Площадь меньшего из квадратов равна 1 см2. Чему равно h?
A) 3 см Б) 3,5 см В) 4 см Г) 4,2 см Д) 4,5 см
17
Тест состоит из 20 вопросов. За каждый правильный ответ начисляется 7 баллов, за каждый неправильный ответ вычитается 4 балла. За каждый вопрос, оставленный без ответа, баллы не начисляются и не вычитаются. Эрик прошёл тест и набрал 100 баллов. Сколько вопросов он оставил без ответа?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
18
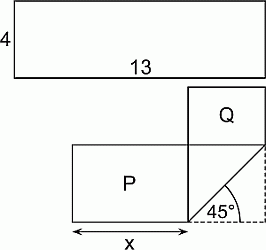
Прямоугольную полоску бумаги размером 4 × 13 согнули, как показано на рисунке. При этом образовались два прямоугольника с площадями P и Q, причём P = 2Q. Чему равен x?
A) 5 Б) 5.5 В) 6 Г) 6.5 Д) 4√2
19
В корзине с фруктами в два раза больше яблок, чем груш. Кристина и Лиля разделили между собой все фрукты так, что у Кристины оказалось в два раза больше фруктов, чем у Лили. Какое из следующих утверждений заведомо верно?
A) У Кристины есть хотя бы одна груша.
Б) У Кристины в два раза больше яблок, чем груш.
В) У Кристины вдвое больше яблок, чем у Лили.
Г) У Кристины столько яблок, сколько у Лили груш.
Д) У Кристины столько груш, сколько яблок у Лили.
20
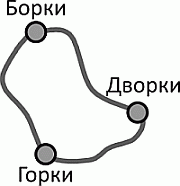
Три деревни соединены дорогами, как показано на рисунке. Путь от Горок до Борок через Дворки на 1 км длиннее дороги, соединяющей Горки и Борки. Путь от Дворок до Борок через Горки на 5 км длиннее дороги, соединяющей Дворки и Борки. Путь от Дворок до Горок через Борки на 7 км длиннее дороги, соединяющей Дворки и Горки. Какова длина самой короткой дороги, соединяющей две из этих трёх деревень?
A) 1 км Б) 2 км В) 3 км Г) 4 км Д) 5 км
21
У некоторой дроби числитель и знаменатель положительны. Числитель увеличили на 40%. На сколько процентов следует уменьшить её знаменатель, чтобы новая дробь стала в два раза больше исходной?
A) 10% Б) 20% В) 30% Г) 40% Д) 50%
22
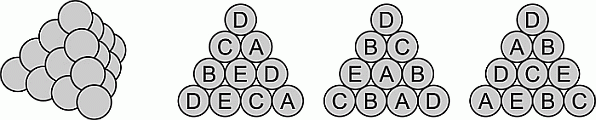
Треугольная пирамида построена из 20 шаров одинакового радиуса. Каждый шар помечен одной из букв A, B, C, D или E. Каждой буквой помечено ровно 4 шара. На рисунках показаны метки шаров на трёх боковых гранях этой пирамиды. Какая метка у центрального шара нижней грани?
A) A Б) B В) C Г) D Д) E
23
Шестизначное число 2ABCDE умножили на 3, и в результате получилось шестизначное число ABCDE2. Какова сумма цифр данного числа?
A) 24 Б) 27 В) 30 Г) 33 Д) 36
24
В коробке находятся только зелёные, красные, синие и жёлтые фишки. Известно, что среди любых 27 произвольно выбранных фишек всегда найдётся хотя бы одна зелёная фишка; среди любых 25 фишек – хотя бы одна красная; среди любых 22 фишек – хотя бы одна синяя; наконец, среди любых 17 фишек – хотя бы одна жёлтая. Какое наибольшее количество фишек может быть в коробке?
A) 27 Б) 29 В) 51 Г) 87 Д) 91
25

Поверхность футбольного мяча состоит из белых шестиугольников и чёрных пятиугольников, как показано на рисунке. Общее количество пятиугольников равно 12. Сколько всего шестиугольников?
A) 12 Б) 15 В) 18 Г) 20 Д) 24
26
2021 кенгуру расставлены в ряд и пронумерованы числами от 1 до 2021. Каждый кенгуру окрашен в красный, серый или синий цвет так, что среди любых трёх подряд стоящих кенгуру встречаются кенгуру всех трёх цветов. Боря угадывал цвета пяти кенгуру и его предположения были: кенгуру 2 – серый; кенгуру 20 – синий; кенгуру 202 – красный; кенгуру 1002 – синий; кенгуру 2021 – серый. Оказалось, что Боря ошибся только один раз. Какой номер кенгуру, цвет которого Боря не угадал?
A) 2 Б) 20 В) 202 Г) 1002 Д) 2021
27
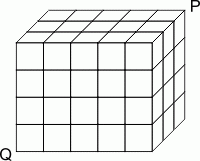
Деревянный параллелепипед размера 3 × 4 × 5 состоит из 60 единичных кубиков. Термит, прогрызая кубики, пробирается по диагонали от вершины Q до вершины P. Эта диагональ не пересекает рёбер ни одного из кубиков. Через сколько кубиков проходит путь термита?
A) 8 Б) 9 В) 10 Г) 11 Д) 12
28
Население города составляет 2021 человек, из которых 2000 лжецов и 21 рыцарь. Лжецы всегда лгут, а рыцари всегда говорят правду. Волшебник разделил 2020 из горожан на 1010 пар. Каждый горожанин в паре назвал другого в своей паре рыцарем или лжецом. В результате, 2000 человек были названы рыцарями, а 20 – лжецами. Сколько было пар, состоящих из двух лжецов?
A) 980 Б) 985 В) 990 Г) 995 Д) 1000
29
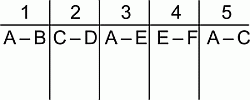
В турнире каждая из шести команд A, B, C, D, E и F сыграла с каждой из остальных один матч, т. е. в каждом из пяти кругов турнира одновременно проходили по три матча. Телеканал решил, что он будет показывать в каждом туре по одному матчу (см. таблицу трансляций матчей, где цифрами обозначены номера кругов). В каком круге турнира команда D играла против команды F?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
30
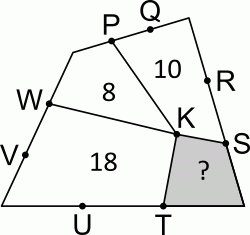
На рисунке изображён четырёхугольник, разбитый на четыре меньших четырёхугольника с общей вершиной K. Остальные отмеченные точки делят стороны большого четырёхугольника на три равные части. Числа, записанные внутри меньших четырёхугольников, указывают их площадь. Чему равна площадь серого четырёхугольника?
A) 4 Б) 5 В) 6 Г) 6,5 Д) 7