1
Сколько простых чисел среди чисел 2, 20, 202 и 2020?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
2
У какого из следующих правильных многоугольников отмеченный угол является наибольшим?

3
Миша, готовясь к олимпиаде, решает 6 задач каждый день, а Лиза – 4 задачи каждый день. Сколько дней понадобится Лизе, чтобы решить столько же задач, сколько решит Миша за 4 дня?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
4
Какая из следующих дробей имеет наибольшее значение?
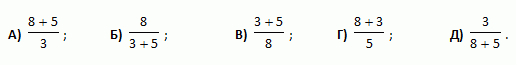
5

Большой квадрат разбит на меньшие квадраты так, как показано на рисунке. А один из квадратов ещё разбит диагональю на два треугольника. Какая по площади часть большого квадрата является серой?
A) 4/5 Б) 3/8 В) 4/9 Г) 1/3 Д) 1/2
6
В футбольном турнире участвуют 4 команды. Каждая команда должна сыграть с каждой один матч. В каждом матче победитель получает 3 очка, а проигравший – 0 очков. В случае ничьей обе команды получают по 1 очку. Какое из следующих чисел не может быть суммой очков, набранных какой-нибудь командой после завершения турнира?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
7
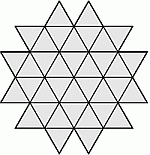
Петя сложил из 36 одинаковых треугольных плиток фигуру на рисунке. Какое наименьшее количество таких плиток ещё нужно добавить, чтобы эта фигура превратилась в шестиугольник?
A) 10 Б) 12 В) 15 Г) 18 Д) 24
8
Ванда хочет перемножить какие-то три различных числа из чисел –5, –3, –1, 2, 4 и 6. Какой наименьший результат она может получить?
A) –200 Б) –120 В) –90 Г) –48 Д) -15
9
Если Женя едет в школу на автобусе, а затем идёт назад пешком, то на дорогу туда и обратно у него уходит 3 часа. А если он едет на автобусе в обе стороны, то он находится в дороге 1 час. Сколько времени понадобится Жене, если он до школы и обратно будет идти пешком?
A) 3,5 часа Б) 4 часа В) 4,5 часа Г) 5 часов Д) 5,5 часа
10
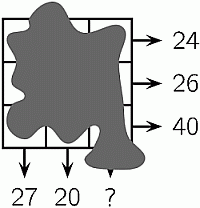
В каждой клетке таблицы 3 × 3 было записано число. К сожалению, таблица оказалась залита чернилами так, что ни одного числа не стало видно. Но суммы чисел в строчках и двух столбцах известны (см. рис.). Чему равна сумма чисел в третьем столбце?
A) 41 Б) 43 В) 44 Г) 45 Д) 47
11
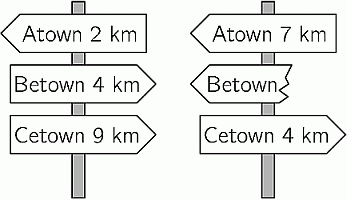
Кратчайший путь от Атауна до Цетауна пролегает через Бетаун. Два указателя показаны на этом пути. Какое расстояние было написано на сломанном знаке?
A) 1 км Б) 3 км В) 4 км Г) 5 км Д) 9 км
12
Анна хочет в марте гулять в среднем 5 км каждый день. 16 марта, перед тем как лечь спать, она подсчитала, что до сих пор она прошла 95 км. Какое расстояние ей нужно в среднем проходить за оставшиеся дни марта для достижения своей цели?
A) 5,4 км Б) 5 км В) 4 км Г) 3,6 км Д) 3,1 км
13
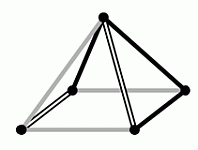
Как выглядит следующая пирамида, если посмотреть на неё сверху?

14
Каждый ученик в классе занимается либо плаванием, либо танцами, либо и тем, и другим. Три пятых учеников класса занимаются плаванием и столько же – танцами. Пять учеников класса занимаются и плаванием, и танцами. Сколько учеников в этом классе?
A) 15 Б) 20 В) 25 Г) 30 Д) 35
15
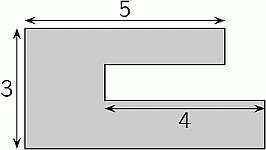
Дедушкин сад имеет форму, показанную на рисунке. Все его стороны параллельны или перпендикулярны друг другу. Некоторые размеры указаны на рисунке. Каков периметр дедушкиного сада?
A) 22 Б) 23 В) 24 Г) 25 Д) 26
16
У Эндрю есть 27 одинаковых маленьких кубиков, у каждого две смежные грани окрашены в красный цвет, остальные грани – белые. Эндрю построил из всех кубиков большой куб. Какое наибольшее количество полностью красных граней может иметь построенный куб?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
17
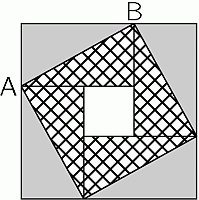
Большой квадрат состоит из четырёх одинаковых прямоугольников и небольшого квадрата в центре. Площадь большого квадрата равна 49 см2, а длина диагонали AB одного из прямоугольников равна 5 см. Какую площадь имеет небольшой квадрат в центре?
A) 1 см2
Б) 2,25 см2
В) 4 см2
Г) 9 см2
Д) 16 см2
18
Зарплата Вернера составляет 20% от зарплаты его босса. На сколько процентов нужно увеличиваться зарплату Вернера, чтобы она стала равна зарплате его босса?
A) 80% Б) 120% В) 180% Г) 400% Д) 500%
19
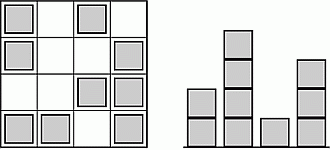
Ирина построила «город» из одинаковых кубиков. На первом из следующих рисунков показан вид «города» сверху, а на втором – вид с одной из сторон, но неизвестно, с какой. Какое наибольшее количество кубиков Ирина могла использовать для построения «города»?
A) 25 Б) 24 В) 23 Г) 22 Д) 21
20

У Маши есть полоска бумаги, разбитая на клетки с числами 1, 2, 3, 4 и 5 в клетках (см. рис.). Она складывает полоску разными способами так, что клетки накрывают друг друга в 5 слоёв. В каком порядке (от верхнего слоя к нижнему) не могут располагаться числа в клетках сложенной полоски?
A) 3, 5, 4, 2, 1
Б) 3, 4, 5, 1, 2
В) 3, 2, 1, 4, 5
Г) 3, 1, 2, 4, 5
Д) 3, 4, 2, 1, 5
21
В ряд расположены двенадцать цветных кубиков: 3 синих, 2 жёлтых, 3 красных и 4 зелёных (но не обязательно в таком порядке). На концах ряда находятся жёлтый и красный кубики. Все красные кубики лежат подряд друг за другом. Все зелёные кубики тоже лежат подряд друг за другом. Десятый слева кубик – синий. Какого цвета шестой слева кубик?
A) зелёного
Б) жёлтого
В) синего
Г) красного
Д) красного или синего
22
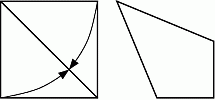
Зина сложила две стороны квадрата по диагонали так, что получился четырёхугольник на рисунке. Чему равна величина максимального угла в полученном четырёхугольнике?
A) 112,5° Б) 120° В) 125° Г) 135° Д) 145°
23
Сколько существует четырёхзначных чисел A, таких, что половина числа A делится на 2, треть числа А делится на 3, а пятая часть А делится на 5?
A) 1 Б) 7 В) 9 Г) 10 Д) 11
24
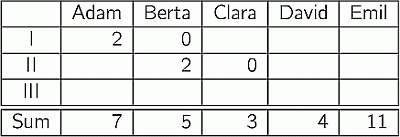
В финале танцевального конкурса каждый из трёх членов жюри присуждает участникам 0, 1, 2, 3 или 4 балла. Ни один судья никаким двум участникам не присуждает одинаковое число баллов. Адам знает суммы баллов всех участников и несколько отдельных оценок, показанных в таблице. Сколько баллов получил Адам от судьи III?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
25
Возле каждой стороны квадрата Светлана записала некоторое натуральное число. Затем возле каждой вершины квадрата она записала произведение чисел возле двух сторон, выходящих из данной вершины. Сумма чисел в вершинах квадрата оказалась равна 15. Чему равна сумма чисел на сторонах квадрата?
A) 6 Б) 7 В) 8 Г) 10 Д) 15
26
У Софии есть 52 одинаковых равнобедренных прямоугольных треугольника. Она хочет из некоторых из них построить квадраты. Сколько существует квадратов различных размеров, которые она может получить?
A) 6 Б) 7 В) 8 Г) 9 Д) 10
27

Коля строит пирамиду из одинаковых шаров. Основание пирамиды квадратное и состоит из 4 × 4 шаров, как показано на рисунке. Следующие слои состоят из 3 × 3 шаров, 2 × 2, а верхний слой состоит из одного шара. В каждой точке соприкосновения двух сфер Коля капнул по капле клея. Сколько всего получилось таких капель?
A) 72 Б) 85 В) 88 Г) 92 Д) 96
28
Четверо мальчиков находятся в четырёх углах бассейна 10 м × 25 м. Их тренер стоит где-то на одной из сторон бассейна. Когда тренер позвал детей, трое из них вышли из бассейна и пошли к нему по сторонам бассейна по кратчайшему пути. Вместе они прошли 50 метров. Какое наименьшее расстояние до тренера нужно пройти четвёртому мальчику?
A) 10 м Б) 12 м В) 15 м Г) 20 м Д) 25 м
29
Андрей, Борис и Василий решили устроить гонку. Они стартовали одновременно и бежали с постоянными скоростями. Когда Андрей финишировал, Борису до финиша оставалось
15 метров, а Василию – 35 метров. А когда Борис финишировал, то Василию оставалось до финиша 22 метра. Какова длина дистанции?
A) 135 м Б) 140 м В) 150 м Г) 165 м Д) 175 м
30
Если сравнить неизвестное четырёхзначное число с некоторыми другими числами, то имеются следующие сведения.
1) 4132 (две цифры правильные, но на неправильных позициях).
2) 9826 (одна цифра правильная и на правильной позиции).
3) 5079 (две цифры верные, но ровно одна из них находится на нужной позиции).
4) 2741 (одна цифра верная, но не на верной позиции).
5) 7642 (ни одна цифра не верна).
Какая цифра является последней у неизвестного числа?
A) 0 Б) 1 В) 3 Г) 5 Д) 9