1
Сколько целых чисел находится между числами 2,016 и 20,16?
A) 15 Б) 16 В) 17 Г) 18 Д) 19
2
Какой из следующих дорожных знаков имеет наибольшее число осей симметрии?

3
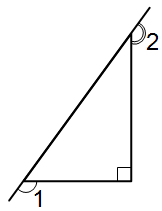
Чему равна сумма двух отмеченных углов 1 и 2 на рисунке?
A) 150° Б) 180° В) 240° Г) 270° Д) 300°
4
Дженни должна была прибавить 26 к некоторому числу. Но вместо этого она вычла 26 из данного числа и получила число -14. Какое число получилось бы, если бы Дженни не перепутала действия?
A) 28 Б) 32 В) 36 Г) 38 Д) 42
5
Жанна перевернула карточку сначала через нижнюю сторону, а затем через правую (см. рис.).
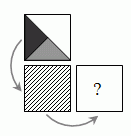
Что в результате получилось?

6
У кенгурёнка имеется 555 кучек по 9 камешков в каждой. Сколько кучек у него получится, если он разложит все камешки в кучки по 5 камешков в каждой?
A) 999 Б) 900 В) 555 Г) 666 Д) 333
7
В моей школе 45 учителей приезжают на работу на велосипеде, что составляет 60% от числа всех учителей. Только 12% учителей приезжают на работу на автомобиле. Сколько учителей приезжает на работу на автомобиле?
A) 4 Б) 6 В) 9 Г) 10 Д) 12
8
Чему равна площадь серой части прямоугольника на рисунке?
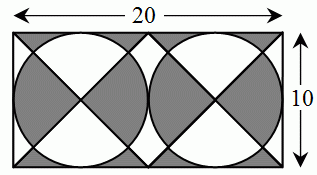
A) 50 Б) 180 В) 100 Г) 120 Д) 150
9
Одна верёвка имеет длину 1 м, а другая – 2 м. Алекс разрезал эти две верёвки на несколько кусков (все куски одной длины). Какое из следующих чисел не может равняться числу полученных кусков?
A) 6 Б) 8 В) 9 Г) 12 Д) 15
10
При проведении конкурса этот вопрос не оценивался или правильными являются два варианта ответа.
Поэтому при тестовом выполнении он пропускается. При проверке своих ответов вы сможете посмотреть и пропущенный вопрос.
11
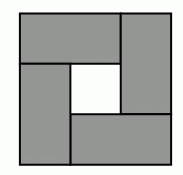
Четыре одинаковых прямоугольника периметра 16 см поместили без наложения в квадрат так, как показано на рисунке. Чему равен периметр этого квадрата?
A) 16 см Б) 120 см В) 24 см Г) 28 см Д) 32 см
12
На ожерелье у Петры 49 синих бусинок и одна красная. Сколько бусинок Петре нужно снять с ожерелья, чтобы число синих бусинок составило 90% от числа всех бусинок на ожерелье?
A) 4 Б) 10 В) 29 Г) 39 Д) 40
13
Какая из следующих дробей ближайшая к числу 0,5?
A) 2579 Б) 2759 В) 2957 Г) 5279 Д) 5792
14
Игорь записал результаты четвертьфинала, полуфинала и финала турнира по боксу с выбыванием (не обязательно в указанном порядке): Боря победил Антона, Коля победил Диму, Гриша победил Сашу, Гриша победил Колю, Коля победил Борю, Эдик победил Федю и Гриша победил Эдика. Кто участвовал в финальном бое?
A) Гриша и Саша
Б) Гриша и Коля
В) Коля и Боря
Г) Гриша и Антон
Д) Коля и Дима
15
Тим, Том и Джим – тройняшки (родились в один день). У них есть два брата-близнеца, младших на 3 года. Какое из следующих чисел может быть суммой лет всех пяти братьев?
A) 36 Б) 53 В) 76 Г) 89 Д) 92
16
Аня склеила из кубиков фигуру, показанную на рисунке.
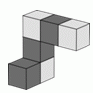
Она поворачивает её, чтобы рассмотреть с разных сторон. Что из указанного в вариантах ответа она не сможет увидеть?
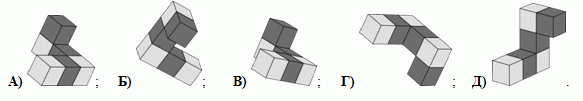
17
У Маши есть бумажная полоска, она с одной стороны белая, с другой – серая. Ширина полоски равна 3 см. Маша согнула полоску так, как показано на рисунке. Чему равна длина полоски?
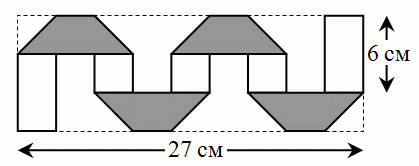
A) 36 см Б) 48 см В) 54 см Г) 57 см Д) 81 см
18
Два кенгуру Джим и Пьер начинают прыгать одновременно с одного и того же места в одном и том же направлении. Каждый из них совершает один прыжок в секунду. Каждый прыжок Джима равен 6 метрам. Пьер сначала прыгает на 1 метр, затем на 2 метра, потом на 3 метра и т.д. Через сколько прыжков Пьер настигнет Джима?
A) 10 Б) 11 В) 12 Г) 13 Д) 14
19

Семь игральных кубиков склеили по граням так, как показано на рисунке и так, что количества точек на каждой из двух склеенных гранях одинаковы. Чему равна сумма точек на поверхности полученного тела?
A) 24 Б) 90 В) 95 Г) 105 Д) 126
20
В классе 20 учащихся. Все они сидят за партами парами так, что ровно треть мальчиков сидит с девочками и ровно половина девочек сидит с мальчиками. Сколько мальчиков в этом классе?
A) 9 Б) 12 В) 15 Г) 16 Д) 18
21
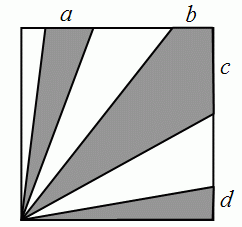
Внутри квадрата площади 36 выделены три белых треугольника. Площадь серой части квадрата равна 27. Стороны серых многоугольников на границе квадрата равны a, b, c и d (см. рис.). Чему равна сумма a + b + c + d?
A) 4 Б) 6 В) 8 Г) 9 Д) 10
22
Часы у Толи опаздывают на 10 мин, но Толя думает, что они на 5 мин спешат. А у Лёни наоборот – часы на 5 мин спешат, но он думает, что они на 10 мин опаздывают. Толя и Лёня одновременно посмотрели каждый на свои часы. Толя думает, что время в этот момент 12:00. Который час в этот момент по мнению Лёни?
A) 11:30 Б) 11:45 В) 12:00 Г) 12:30 Д) 12:45
23
Двенадцать девочек встретились в кафе. В среднем все они съели по 1,5 пирожных. Двое из девочек пили только минеральную воду, а каждая из остальных съела целое число пирожных, но не больше двух. Сколько девочек съели по 2 пирожных?
A) 2 Б) 5 В) 6 Г) 7 Д) 8
24
Курьер-сладкоежка доставляет пирожные на дом некоторым бабушкам, всем одинаковое количество. Но непосредственно перед тем, как зайти к каждой из бабушек, сладкоежка съедает половину имеющихся у него пирожных. После посещения третьей бабушки у сладкоежки не осталось ни одного пирожного. На какое из следующих чисел наверняка делится число пирожных, которое у него было вначале?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
25

Куб состоит из 64 кубиков. Сначала ровно один из них чёрный (см. рис.). Через минуту все белые кубики, у которых есть соседний по грани чёрный кубик, становятся чёрными. Через следующую минуту – то же самое. Сколько чёрных кубиков будет через 2 минуты?
A) 11 Б) 13 В) 15 Г) 16 Д) 17
26
На доске записано несколько различных натуральных чисел. Произведение двух наименьших из них равно 16, а произведение двух наибольших равно 225. Чему равна сумма всех записанных на доске чисел?
A) 38 Б) 42 В) 44 Г) 58 Д) 343
27
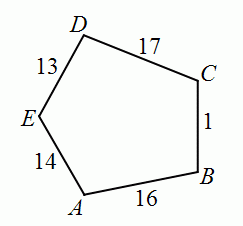
Петя построил 5 окружностей с центрами в вершинах A, B, C, D и E пятиугольника ABCDE. Длины его сторон указаны на рисунке. Любые две окружности с центрами в концах одной стороны касаются друг друга. Какая из вершин данного пятиугольника является центром наибольшей окружности?
A) A Б) B В) C Г) D Д) E
28

Катя записала различные натуральные числа на каждом из четырнадцати кубиков пирамиды на рисунке. Сумма чисел на девяти кубиках в основании пирамиды равна 50. На каждом из кубиков, расположенных выше основания, число равно сумме чисел на тех четырёх кубиках, на которых он стоит. Какое наибольшее значение может иметь число на верхнем кубике пирамиды?
A) 80 Б) 98 В) 104 Г) 110 Д) 118
29
Поезд состоит из пяти вагонов, в каждом вагоне едет по крайней мере один пассажир. Двух пассажиров будем называть соседями, если они едут в одном вагоне или в двух соседних вагонах. У каждого пассажира в поезде имеется либо 5, либо 10 соседей. Сколько пассажиров едет в поезде?
A) 13
Б) 15
В) 17
Г) 20
Д) существует более одного возможного значения
30
Куб 3х3х3 построен из 15 чёрных и 12 белых кубиков одинакового размера. На рисунке показаны пять граней этого куба.
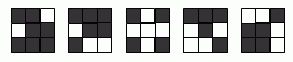
Как выглядит его шестая грань?
