1
Каждый год днём проведения конкурса «Кенгуру» является третий четверг марта. Назовите самую позднюю возможную дату проведения конкурса.
A) 14 марта
Б) 15 марта
В) 20 марта
Г) 21 марта
Д) 22 марта
2
Сколько всего различных четырёхугольников можно насчитать на следующем рисунке?
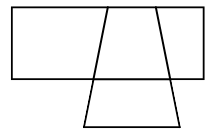
A) 5 Б) 6 В) 7 Г) 8 Д) 9
3
Найдите значение выражения 2014·2014:2014-2014.
A) 0 Б) 1 В) 2013 Г) 2014 Д) 4028
4
В прямоугольник, площадь которого равна 10 см2, вписан четырёхугольник, так, что его вершины являются серединами сторон данного прямоугольника. Найдите площадь вписанного четырёхугольника.
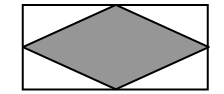
A) 2,5 см2 Б) 4 см2 В) 5 см2 Г) 6 см2 Д) 7,5 см2
5
Произведение двух чисел равно 18, а их сумма равна 19. Чему равна разность этих чисел?
A) 1 Б) 3 В) 7 Г) 10 Д) 17
6
Ванда разрезала несколько квадратов площади 4 так, как показано на рис. 1, и из нескольких полученных кусков сложила фигуру «птица», показанную на рис. 2. Чему равна площадь «птицы»?
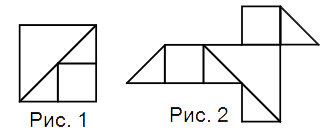
A) 2 Б) 12 В) 10 Г) 5 Д) 6
7
Ведро было наполовину заполнено водой. Бабушка долила в него ещё 2 литра воды, и ведро стало заполнено на три четверти. Какова вместимость ведра?
A) 10 л Б) 9 л В) 8 л Г) 6 л Д) 4 л
8
Жора склеил из 7 единичных кубиков фигуру, показанную на рисунке. Сколько ещё таких кубиков нужно добавить к этой фигуре, чтобы получился куб с ребром 3?
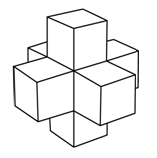
A) 12 Б) 14 В) 16 Г) 18 Д) 20
9
Какое из следующих произведений является наибольшим?
A) 44·777 Б) 55·666 В) 77·444 Г) 88·333 Д) 99·222
10
Ожерелье на рисунке состоит из черных и белых жемчужин. Аня решила снимать по одной жемчужине – каждый раз с любого из концов ожерелья. Как только Аня сняла пятую чёрную жемчужину, она остановилась. Какое наибольшее число белых жемчужин она при этом могла снять?

A) 4 Б) 5 В) 6 Г) 7 Д) 8
11
С начала учебного года Дима и Аня начали заниматься фортепиано: Дима – по два урока в неделю, а Аня – по одному уроку через неделю. Сколько недель должно пройти, чтобы Дима посетил на 15 уроков больше, чем Аня?
A) 30 Б) 25 В) 20 Г) 15 Д) 10
12
На столе лежат 5 кругов (см. рис), площадь каждого равна 1 см2. Общая площадь покрытая любыми двумя соседними кругами равна 1/8 см2. Чему равна площадь той части стола, которая покрыта кругами?
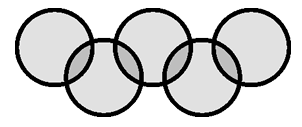
A) 4 см2 Б) 9/2 см2 В) 35/8 см2 Г) 39/8 см2 Д) 19/4 см2
13
В этом году бабушка, её дочь и её внучка заметили, что сумма их возрастов составляет 100 лет, причём возраст каждой является степенью числа 2. Сколько лет внучке? (Возраст равен целому числу лет.)
A) 1 Б) 2 В) 4 Г) 8 Д) 16
14
Пять одинаковых прямоугольников расположены внутри квадрата со стороной 24 см так, как показано на рисунке. Какую площадь имеет каждый из этих прямоугольников?
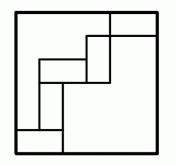
A) 12 см2 Б) 16 см2 В) 18 см2 Г) 24 см2 Д) 32 см2
15
В двух из семи зон на диаграмме изображены «сердце» и «стрела». За один шаг «сердце» перемещается на 3 зоны по ходу часовой стрелки, а «стрела» – на 4 зоны против хода часовой стрелки. Через какое наименьшее число ходов «стрела пронзит сердце» (т.е. они окажутся в одной и той же зоне)?
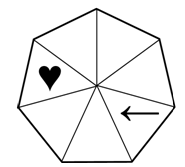
A) 7 Б) 8 В) 9 Г) 10 Д) никогда
16
В треугольнике ABC биссектриса AD пересекается с высотой BH в точке M, а ∠AMB = 2 · ∠CAB. Найдите ∠CAB.
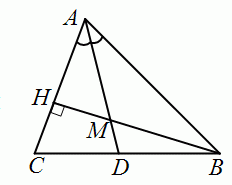
A) 30° Б) 45° В) 60° Г) 75° Д) 90°
17
Шестеро студентов снимают квартиру, в которой есть две ванные комнаты. Студенты просыпаются и начинают умываться ровно с 7:00. На это у них уходит 8, 10, 12, 17, 21 и 22 минуты соответственно. Никакие двое не могут пользоваться одной и той же ванной одновременно. Сразу после того, как умылся последний, студенты садятся завтракать. В какое самое раннее время может начаться их завтрак?
A) 7:45 Б) 7:46 В) 7:47 Г) 7:48 Д) 7:50
18
Стороны прямоугольника равны 6 см и 11 см. Из двух концов одной из бóльших сторон проведены биссектрисы углов данного прямоугольника, которые делят противоположную сторону на три части. Найдите длины этих частей.
A) 1 см, 9 см, 1 см
Б) 2 см, 7 см, 2 см
В) 3 см, 5 см, 3 см
Г) 4 см, 3 см, 4 см
Д) 5 см, 1 см, 5 см
19
Несколько пиратов нашли клад, состоящий из одинаковых золотых монет, и разделили находку поровну между собой. Если бы пиратов было на 4 меньше, то каждому досталось бы на 10 монет больше. А если бы монет было на 50 меньше, то каждый получил бы на 5 монет меньше. Из какого числа монет состоял клад?
A) 80 Б) 100 В) 120 Г) 150 Д) 200
20
Среднее арифметическое двух чисел на 30% меньше одного из них. На сколько процентов среднее арифметическое больше другого из этих двух чисел?
A) 75% Б) 70% В) 60% Г) 30% Д) 25%
21
Максим вписал каждое из чисел от 1 до 9 в клетки таблицы 3×3. На рисунке можно видеть только четыре из вписанных чисел. Максим подсчитал, что для числа 9 сумма чисел в соседних по стороне клетках равна 15. Чему равна сумма чисел в соседних по стороне клетках у числа 8?
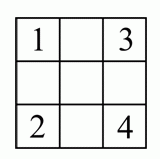
A) 12 Б) 18 В) 20 Г) 26 Д) 27
22
Старые весы не работают должным образом. Если предмет весит менее 1000 г, весы показывают правильный вес. В противном случае, если предмет весит 1000 г или более, они могут показать любой вес, больший 1000 г. У нас имеется 5 предметов, весящих А г, В г, С г, D г и Е г, каждый меньше 1000 г. При их взвешивании парами на данных весах были получены результаты:B+D=1200, C+E=2100, B+E=800, B+C=900, A+E=700. Какой из этих предметов имеет самый большой вес?
A) A Б) B В) C Г) D Д) E
23
На доске записаны несколько различных натуральных чисел. Ровно 2 из них делятся на 2, и ровно 13 из них делятся на 13. Пусть M – наибольшее из этих чисел. Какое наименьшее значение может принимать M?
A) 169 Б) 260 В) 273 Г) 299 Д) 325
24
Лиза и Маша соревнуются в решении задач. У них имеются одинаковые комплекты из 100 задач. За каждую задачу та девочка, которая решила её первой, получает 4 балла, а та, которая решила её второй – 1 балл. За нерешённые задачи баллы не начисляются. Лиза решила 60 задач, и Маша также решила 60 задач. Вместе они получили 312 баллов. Сколько было таких задач, которые решила каждая из девочек?
A) 53 Б) 54 В) 55 Г) 56 Д) 57
25
Дима едет на велосипеде от дома до дачи, куда он планирует прибыть в 15:00. Но за 2/3 запланированного времени он преодолел 3/4 всего расстояния. После этого Дима поехал медленнее и прибыл на дачу вовремя. Каково отношение средней скорости на первой части маршрута к средней скорости на второй части маршрута?
A) 5:4 Б) 4:3 В) 3:2 Г) 2:1 Д) 3:1
26
Четыре идентичных (по размеру и окраске) кубика на рис. 1 можно сложить в блок так, что на переднем плане будет рисунок, показанный на рис. 2. Какой рисунок будет на обратной стороне этого блока?
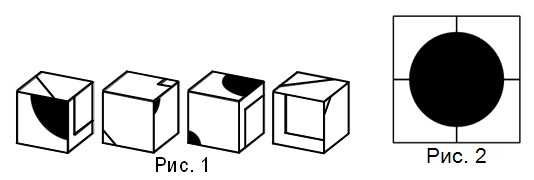

27
В группе 25 человек. Её составляют правдивые (всегда говорят правду), лжецы (всегда лгут) и шутники (чередуют правду и ложь). Когда каждого из них спросили: "Ты – правдивый?", 17 человек ответили: "Да". Затем, когда каждого спросили: "Ты – шутник?", 12 ответили: "Да". Наконец, когда каждого спросили: "Ты – лжец?", 8 ответили: "Да". Сколько правдивых в этой группе?
A) 4 Б) 5 В) 9 Г) 13 Д) 17
28
В четырёхугольнике ABCD (см. рис.) диагональ BD равна 8 см, ∠BAC=∠BCA=∠CDB=∠BDA=45°. Найдите площадь ABCD.
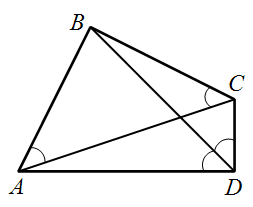
A) 30 см2 Б) 32 см2 В) 35 см2 Г) 40 см2 Д) 48 см2
29
На поверхности водоёма 16 листьев кувшинок образуют квадрат 4×4. На одном листе сидит лягушка (см. рис.). Она совершает прыжки по вертикали или по горизонтали, каждый раз перепрыгивая не менее чем через один лист, и никогда не прыгает на тот лист, на котором она уже была. На каком наибольшем количестве этих листьев, включая и исходный, она может побывать?
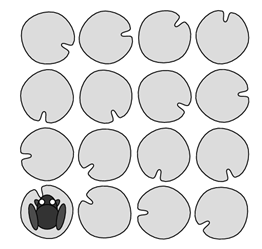
A) 16 Б) 15 В) 14 Г) 13 Д) 12
30
Квадрат 5×5 построен из единичных плиток указанного на рисунке вида. Любые две плитки соприкасаются сторонами одинакового цвета. Периметр квадрата 5×5, тем самым, состоит из чёрных и белых единичных отрезков. Какое наименьшее число чёрных отрезков может среди них быть?

A) 4 Б) 5 В) 6 Г) 7 Д) 8