1
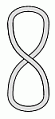
Какую из следующих верёвок нельзя преобразовать, не разрезая, в веревку на рисунке сверху?
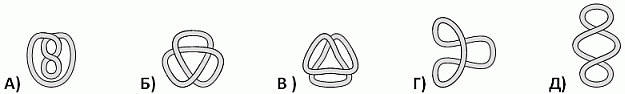
2
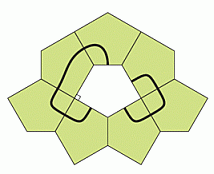
Фигура на рисунке сверху состоит из пятиугольных плиток одинакового размера. Какую из следующих плиток нужно поместить в центр данной фигуры, чтобы на её поверхности появились две замкнутые кривые?

3
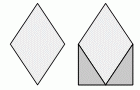
К ромбу на рисунке добавили два прямоугольных треугольника. На сколько процентов увеличилась площадь фигуры?
A) 20% Б) 25% В) 30% Г) 40% Д) 50%
4
Чему равно значение выражения
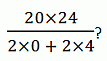
A) 12 Б) 30 В) 48 Г) 60 Д) 120
5
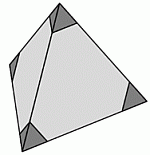
Юля отрезала четыре вершины тетраэдра, как показано на рисунке. Сколько вершин стало у получившегося многогранника?
A) 8 Б) 9 В) 11 Г) 12 Д) 15
6
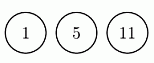
У Риты есть три жетона с числами 1, 5 и 11. Она хочет разместить их в ряд, чтобы получилось четырёхзначное число. Сколько различных четырёхзначных чисел она сможет так составить?
A) 3 Б) 4 В) 6 Г) 8 Д) 9
7
В вазе лежат фрукты:  .
.
Аня любит  .
.
Боря любит  .
.
Вале нравятся  .
.
Гале нравится  .
.
Дима любит  .
.
Фрукты распределили так, что каждому достался тот фрукт, который нравится. Кто получил  ?
?
A) Аня Б) Боря В) Валя Г) Галя Д) Дима
8
Лифт может перевозить либо не более 12 взрослых, либо не более 20 детей. Какое наибольшее число детей может перевезти лифт вместе с 9 взрослыми?
A) 3 Б) 4 В) 5 Г) 6 Д) 8
9
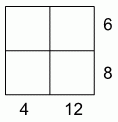
Впишите четыре различных натуральных числа в клетки таблицы так, чтобы произведения чисел в строчках и столбцах равнялись указанным на рисунке значениям. Чему равна сумма этих четырёх чисел?
A) 10 Б) 12 В) 13 Г) 14 Д) 15
10

Длина комплекта из четырёх компактно упакованных тележек в супермаркете равна 108 см. Длина такого же комплекта из десяти тележек равна 168 см. Чему равна длина одной тележки?
A) 60 см Б) 68 см В) 78 см Г) 88 см Д) 90 см
11
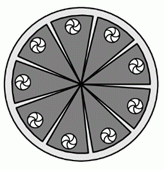
Карина испекла пирог и разрезала его на десять равных частей. Она съела одну часть, а затем равномерно раздвинула остальные части, так, чтобы края соседних частей образовали равные углы. Чему равна величина одного такого угла?
A) 5° Б) 4° В) 3° Г) 2° Д) 1°
12
Вернер строит квадрат 4 × 4. У него имеются три фрагмента, изображённые на рисунке.
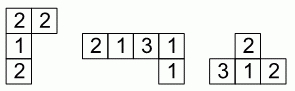
Какой ещё один фрагмент ему нужно добавить, чтобы в построенном квадрате суммы чисел во всех строчках и столбцах были одинаковы?

13
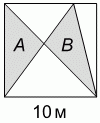
Квадрат разбит на части тремя отрезками прямых линий, как показано на рисунке. Сторона квадрата равна 10 м. Площади двух серых треугольников равны А и B. Чему равна разность A – B?
A) 0 м2
Б) 1 м2
В) 2 м2
Г) 5 м2
Д) 10 м2
14
Пингвин Паша каждый день ходит на рыбалку и всегда приносит 12 рыбок для своих двух птенцов. Каждый раз он даёт первому увиденному птенцу 7 рыбок, а другому – 5. Птенцы сразу полученные рыбки съедают. За последние несколько дней один из птенцов съел 44 рыбки. Сколько рыбок съел за это же время другой птенец?
A) 34 Б) 40 В) 46 Г) 52 Д) 58
15
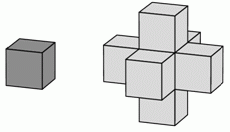
У Джона есть много одинаковых кубиков. Он взял один кубик и приклеил ко всем его граням на поверхности по одному кубику. Далее, Джон хочет к каждой грани на поверхности построенной конструкции таким же образом приклеить по кубику. Сколько кубиков ему для этого понадобится?
A) 18 Б) 16 В) 14 Г) 12 Д) 10
16
Кенгуру прыгает вверх на вершину горы, а затем прыгает обратно по тому же маршруту и финиширует в точке старта. Прыжок вверх у кенгуру равен 1 м, а прыжок вниз – 3 м. Всего кенгуру совершил 2024 прыжка. Какова общая длина пути, пройденного кенгуру прыжками?
A) 506 м Б) 1012 м В) 2024 м Г) 3036 м Д) 4048 м
17

Дима разрезал прямоугольник на четыре меньших прямоугольника, как показано на рисунке. Периметры трёх из них равны 16, 18 и 24. Чему равен периметр четвёртого прямоугольника?
A) 8 Б) 10 В) 12 Г) 14 Д) 16
18
Свежие грибы содержат 80% воды. После сушки грибы содержат только 20% воды. На сколько процентов уменьшается масса грибов при сушке?
A) на 60%
Б) на 70%
В) на 75%
Г) на 80%
Д) на 85%
19
Плиточник Терри хочет выложить большой квадратный пол с повторяющимся мозаичным узором. Он складывает шестиугольные и треугольные плитки так, как показано на рисунке.

Терри предполагает, что на всю работу ему понадобится 3000 шестиугольных плиток. Сколько примерно понадобится ему треугольных плиток?
A) 1000 Б) 1500 В) 3000 Г) 6000 Д) 9000
20
На столе лежали девять карточек с числами от 1 до 9. Алексей, Боря, Валя и Галя взяли по две карточки. Алексей сказал: «Сумма чисел на моих карточках равна 6». Боря сказал: «Разница между числами на моих карточках равна 5». Валя сказала: «Произведение чисел на моих карточках равно 18». Галя сказала: «Одно из чисел на моих карточках в два раза больше другого». Все четверо сделали верные заявления. Какое число на карточке, которая осталась на столе?
A) 1 Б) 3 В) 6 Г) 8 Д) 9
21

Цифры 0 – 9 можно изобразить с помощью горизонтальных и вертикальных сегментов, как показано на рисунке. Гриша выбрал три разные цифры. Всего его цифры имеют 5 горизонтальных и 10 вертикальных сегментов. Чему равна сумма трёх выбранных Гришей цифр?
A) 9 Б) 10 В) 14 Г) 18 Д) 19
22

Толя хочет закрасить чёрным цветом ещё две клетки в квадрате на рисунке так, чтобы полученный в результате узор (т.е. весь квадрат с учётом раскраски) имел единственную ось симметрии. Сколько различных способов есть, чтобы это сделать?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
23
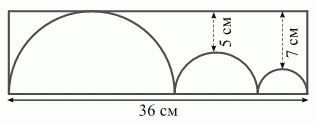
Три полукруга вписаны в прямоугольник так, как показано на рисунке. Чему равен периметр данного прямоугольника?
A) 82 см Б) 92 см В) 96 см Г) 108 см Д) 120 см
24
50 учеников стоят по кругу и бросают мяч. Каждый, кто получил мяч, бросает его шестому от него (против хода часовой стрелки) ученику. Федя поймал мяч 100 раз. Сколько учеников за это время не поймали мяч ни разу?
A) 0 Б) 8 В) 10 Г) 25 Д) 40
25
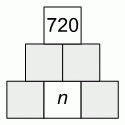
Дима хочет заполнить клетки диаграммы натуральными числами так, чтобы выполнялось условие: каждое число в средней и верхней строчке равно произведению двух соседних по стороне нижестоящих чисел. В верхней клетке должно быть число 720. Сколько различных значений может иметь число n?
A) 1 Б) 4 В) 5 Г) 6 Д) 8
26
Фермер Фай продаёт куриные и утиные яйца. У него есть 6 коробок, содержащих 4, 6, 12, 13, 22 и 29 яиц. Первый покупатель купил все яйца одной из коробок. Фай заметил, что число куриных яиц, которые у него остались, в два раза больше числа утиных яиц. Сколько яиц купил покупатель?
A) 4 Б) 12 В) 13 Г) 22 Д) 29
27
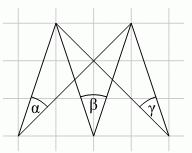
На клетчатой бумаге отмечены углы α, β и γ так, как показано на рисунке. Чему равна их сумма α + β + γ?
A) 60° Б) 70° В) 75° Г) 90° Д) 120°
28
Капитан Флинт попросил четырёх своих пиратов написать на листе бумаги, сколько золотых, серебряных и бронзовых монет находилось в сундуке с сокровищами. Их ответы показаны на рисунке.
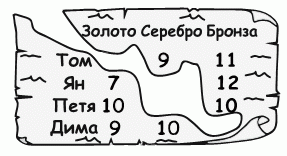
Как видим, часть бумаги с ответами повреждена. Кроме того известно, что только один из четырёх пиратов сказал правду. Три другие пирата солгали по всем трём пунктам. Всего в сундуке было 30 монет. Кто сказал правду?
A) Tом
Б) Ян
В) Петя
Г) Дима
Д) невозможно определить
29
Алекс выезжает из пункта А в пункт В, затем сразу возвращается в А. Одновременно Боб выезжает из пункта В в пункт А, затем сразу же возвращается в В. Скорость Алекса в три раза больше скорости Боба. Первый раз они встречаются через 15 минут после старта. Через сколько минут после старта они встретятся второй раз?
A) 20 мин Б) 25 мин В) 30 мин Г) 35 мин Д) 45 мин
30
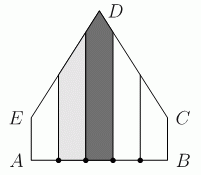
В пятиугольнике ABCDE:
∠A = ∠B = 90°, АЕ = ВС и ED = DC.
На стороне АВ отметили четыре точки, которые делят её на пять равных частей. Затем через эти точки провели перпендикуляры к данной стороне, как показано на рисунке. Чёрная часть пятиугольника имеет площадь 13 см2, а серая – 10 см2. Чему равна площадь всего пятиугольника?
A) 45 см2
Б) 47 см2
В) 49 см2
Г) 58 см2
Д) 60 см2