1
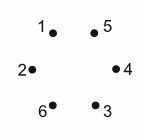
Шесть точек пронумерованы, как показано на рисунке. Сначала Кристина соединила отрезками точки с чётными номерами и получила один треугольник. Затем она соединила отрезками точки с нечётными номерами и получила другой треугольник. Один треугольник она окрасила в чёрный цвет, а другой – в серый. В каком из следующих ответов изображены построенные Кристиной треугольники?

2
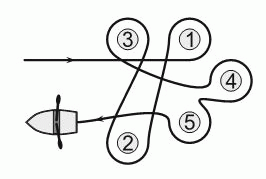
Лена проплыла на лодке вокруг пяти буёв, как показано на рисунке. Какие буи она огибала против хода часовой стрелки?
A) 1 и 4
Б) 2, 3 и 5
В) 2 и 3
Г) 1, 4 и 5
Д) 1 и 3
3
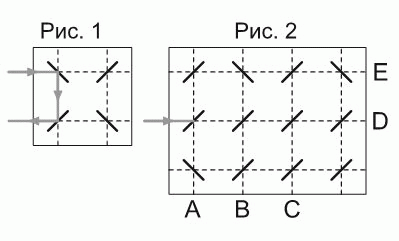
Луч лазера отражается от зеркал так, как показано на рисунке 1. В какой точке выйдет луч лазера на втором рисунке 2?
A) A Б) B В) C Г) D Д) E
5
Шарики продаются в пакетах по 5, 10 или 25 штук. Том купил ровно 95 шариков. Какое наименьшее количество пакетов, он мог купить?
A) 4 Б) 5 В) 7 Г) 8 Д) 10
6
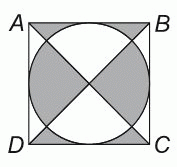
Сторона квадрата ABCD равна 10 см. Чему равна площадь серой части этого квадрата?
A) 40 см2 Б) 45 см2 В) 50 см2 Г) 55 см2 Д) 60 см2
7
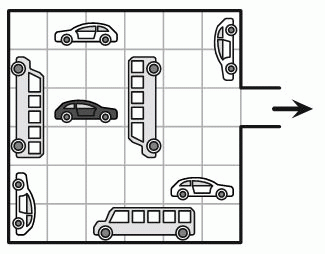
В гараже на рисунке автомобили могут двигаться только вперёд или назад, но не могут поворачивать. Какое наименьшее количество автомобилей должно переместиться, чтобы чёрный автомобиль мог выехать из гаража?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
8
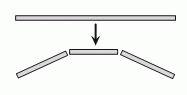
Юля хочет приготовить спагетти. У неё есть одна длинная нить спагетти, которую ей нужно разломать. Первый раз она ломает её на 3 части. Далее некоторые из образовавшихся кусков она каждый раз также ломает на 3 части. Какое из следующих чисел НЕ МОЖЕТ быть числом кусков, которые в результате могли получиться у Юли?
A) 13 Б) 17 В) 20 Г) 23 Д) 25
9

Боря сложил в некотором порядке следующие 7 плиток с числами так, что у него получилось 12-значное число. Какими тремя цифрами заканчивается наименьшее из чисел, которые могли получиться у Бори?
A) 699 Б) 113 В) 551 Г) 967 Д) 459
10
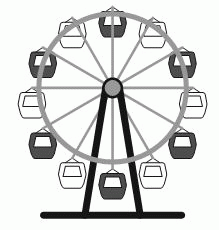
На какую наименьшую часть оборота должно повернуться колесо обозрения, чтобы наверху оказалась белая кабинка?
A) 1/2 Б) 1/3 В) 1/6 Г) 1/12 Д) 5/6
11
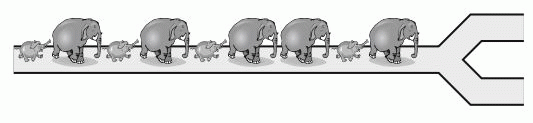
Пять слонов и четыре слонёнка идут друг за другом по тропинке, как показано на рисунке. На развилке каждый из них поворачивает либо налево, либо направо. В какой последовательности они НЕ МОГУТ идти после развилки?
A) 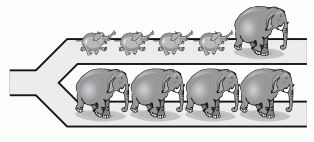
Б) 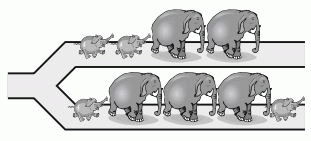
В) 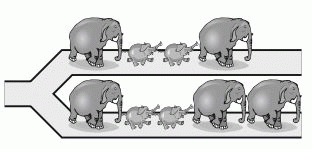
Г) 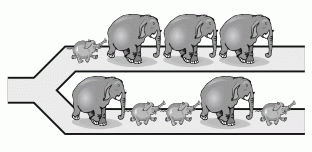
Д) 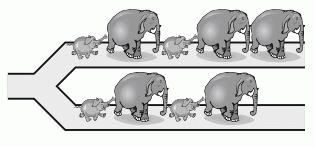
12
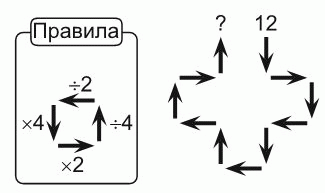
Клара начала с числа 12 и, продвигаясь по стрелкам, преобразует его согласно правилам. Что у неё получится в результате?
A) 13 Б) 6 В) 12 Г) 24 Д) 48
13
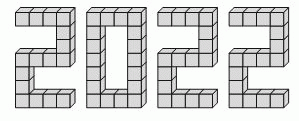
Миша и его друзья склеили число 2022 из 66 кубиков, как показано на рисунке. Они окрасили поверхности всех получившихся цифр в серый цвет. У какого числа кубиков оказались окрашены ровно 4 грани?
A) 16 Б) 30 В) 46 Г) 54 Д) 60
14
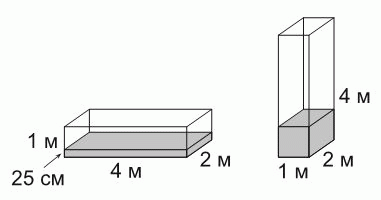
Резервуар для воды прямоугольной формы имеет размеры 1м x 2м x 4м. На первом рисунке уровень воды в резервуаре равен 25 см. Каков уровень такого же объёма воды в этом резервуаре на втором рисунке?
A) 25 см Б) 50 см В) 75 см Г) 1 м Д) 1,25 м
15
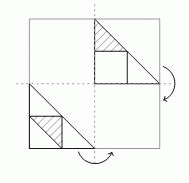
На рисунке показан прозрачный лист бумаги с рисунком на нём. Лист согнули дважды так, как показано на рисунке. Как он может выглядеть после этого?

16
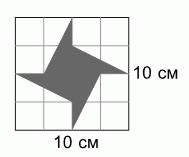
Площадь квадрата на рисунке равна 100 см2. Какую площадь имеет его окрашенная часть?
A) 20 см2 Б) 25 см2 В) 30 см2 Г) 35 см2 Д) 40 см2
17
Для черепахи Евы 2022 год уже третий со дня её рождения, в записи которого есть три одинаковые цифры. Какое наименьшее число лет может быть Еве к концу этого года?
A) 18 Б) 20 В) 22 Г) 23 Д) 134
18
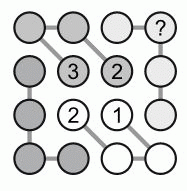
Андрей хочет заполнить пустые кружочки таблицы так, чтобы в каждой строке, каждом столбце и каждой четвёрке кружочков, соединенных отрезками, были числа 1, 2, 3 и 4. Какое число он должен записать в кружке со знаком вопроса?
A) 1 Б) 2 В) 3 Г) 4 Д) невозможно определить
19
У Лизы есть 4 собаки. Каждая из них весит целое число килограммов. Вместе все они весят 60 кг. Все собаки разные по весу. Вторая по весу (в порядке убывания) собака весит 28 кг. Сколько весит третья (в порядке убывания веса) собака?
A) 2 кг Б) 3 кг В) 4 кг Г) 5 кг Д) 6 кг
20
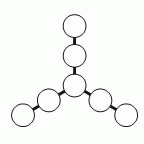
Алеся хочет вписать в кружочки на рисунке числа 3, 4, 5, 6, 7, 8 и 9 так, чтобы суммы всех троек чисел, расположенных на одной прямой, были одинаковыми. Какое наибольшее значение может иметь сумма чисел одной такой тройки чисел?
A) 28 Б) 18 В) 22 Г) 16 Д) 20
21
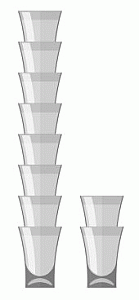
Стаканы вставляют друг в друга (см. рис.). Стопка из 8 стаканов имеет высоту 42 см, а стопка из 2 стаканов – 18 см. Какую высоту имеет стопка из 6 стаканов?
A) 22 см Б) 24 см В) 38 см Г) 34 см Д) 40 см
22
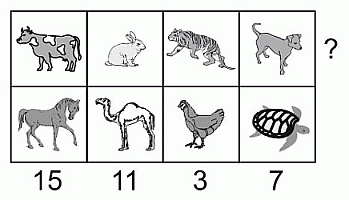
Каждое животное в таблице представляет некоторое натуральное число, разные животные – разные числа. Суммы чисел в столбцах указаны под соответствующими столбцами. Какое наибольшее значение может иметь сумма чисел в первой строке таблицы?
A) 18 Б) 19 В) 20 Г) 21 Д) 22
23
Определите правильный код замка по следующим подсказкам.
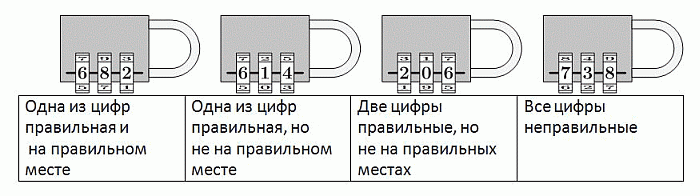
A) 604 Б) 082 В) 640 Г) 042 Д) 046
24
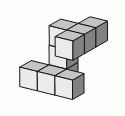
Аня склеила из кубиков фигуру на рисунке. С какой из следующих фигур она совпадает?

25
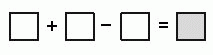
Вернер вписывает числа 2, 3, 4, 5 и 6 в клетки на рисунке так, чтобы получилось правильное равенство. Сколько из этих чисел могут быть вписаны в серую клетку?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
26
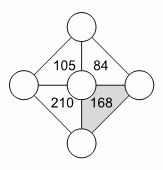
В кружочки в таблице нужно вписать числа 3, 4, 5, 6 и 7 так, чтобы произведения чисел в вершинах треугольников были такими, как указано на рисунке. Чему равна сумма чисел в вершинах окрашенного треугольника?
A) 12 Б) 14 В) 15 Г) 17 Д) 18
27
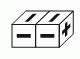
Какой из следующих развёрток НЕ МОЖЕТ быть развёртка параллелепипеда на рисунке сверху?

28
Четыре деревни A, B, C и D расположены вдоль дороги в указанном порядке. Расстояние между соседними деревнями равно 10 км. В деревне A живут 10 школьников, в деревне B – 20 школьников, в деревне C – 30 школьников, в деревне D – 40 школьников. Где нужно построить школу, чтобы сумма расстояний до школы у всех этих школьников была наименьшей?
A) в А
Б) в В
В) посередине между В и С
Г) в С
Д) в D
29
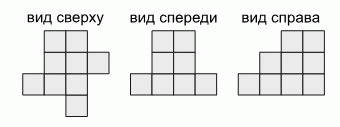
Из одинаковых кубиков построили некоторую конструкцию. На рисунке показан вид этой конструкции сверху, спереди и справа. Какое наибольшее количество кубиков могло быть использовано для построения данной конструкции?
A) 18 Б) 19 В) 20 Г) 21 Д) 22
30
За круглым столом сидят 30 человек. Некоторые из них в шляпе. Те, кто носит шляпу, всегда говорят правду, а те, кто не носит шляпу, могут лгать или говорить правду. Каждый говорит: «По крайней мере, один из двух моих соседей слева и справа не носит шляпы». Какое наибольшее число людей, сидящих за столом, может носить шляпу?
A) 5 Б) 10 В) 15 Г) 20 Д) 25