1

Какой из следующих блоков можно сложить из данных шести кирпичей?

2

Сколько пар детей на рисунке держат друг друга за левую руку?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
3
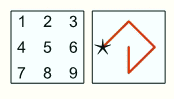
В квадрате на первом рисунке записаны цифры от 1 до 9. Будем строить число, начиная с цифры, указанной звездочкой, и последовательно записывая цифры, расположенные по ходу некоторой линии. Например, линия на втором рисунке задаёт число 42685. Какая из следующих линий задаёт наибольшее число?

4
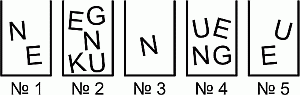
Софья хочет составить слово KENGU из букв, находящихся в коробках. Она может взять только одну букву из каждой коробки. Какую букву Софья должна взять из коробки №4?
A) K Б) E В) N Г) G Д) U
5

Если правильно сложить 5 плиток пазла, получится прямоугольник с примером на сложение. Чему равен результат вычислений в этом примере?
A) 22 Б) 32 В) 41 Г) 122 Д) 203
6
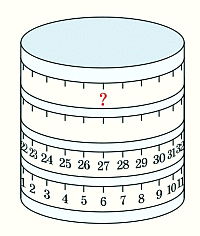
На цилиндр намотали мерную ленту, как показано на рисунке. Какое число стоит на месте, обозначенном знаком вопроса?
A) 53 Б) 60 В) 69 Г) 77 Д) 81
7
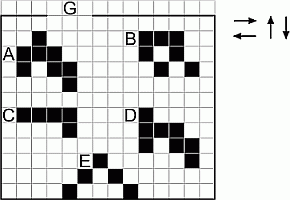
Пять фигур на клетчатой поверхности могут перемещаться только в направлениях, указанных стрелками. Какая из них может выйти через ворота G?
A) A Б) B В) C Г) D Д) E
8
Карина собирается покрасить стены в своей комнате в зелёный цвет. Зелёная краска слишком тёмная, поэтому она решила смешать её с белой краской. Какая из следующих смесей даст самый светлый зелёный цвет?
A) 1 часть зелёной + 3 части белой
Б) 2 части зелёной + 6 частей белой
В) 3 части зелёной + 9 частей белой
Г) 4 части зелёной + 12 частей белой
Д) все смеси дают один и тот же цвет
9
У Марии был лист бумаги. Она сложила его ровно пополам. Потом снова сложила ровно пополам. В результате получился треугольник:  .
.
Какой из следующих могла быть исходная форма листа?
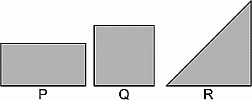
A) только P
Б) только Q
В) только R
Г) только P и Q
Д) любая из указанных
10
Внутри квадрата нарисованы отрезки. Концами отрезков, помимо одной вершины, являются середины других отрезков или сторон квадрата. В каком из следующих ответов окрашена восьмая часть площади данного квадрата?

11
На полоске бумаги было записано число 5021972970. Юля разрезала полоску на три части так, что получилось три числа. Какую наименьшую сумму могли иметь эти три числа?
A) 3244 Б) 3444 В) 5172 Г) 5217 Д) 5444
12
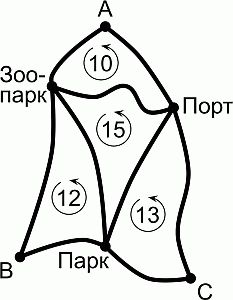
A, B и C на карте – автобусные станции. Круговой маршрут, соединяющий станцию А с зоопарком и портом, составляет 10 км. Круговой маршрут, соединяющий станцию B с парком и зоопарком, составляет 12 км. Круговой маршрут, соединяющий станцию C с портом и парком, составляет 13 км. А круговой маршрут, соединяющий зоопарк, парк и порт, имеет протяженность 15 км. Какова длина кругового маршрута, соединяющего все станции? (Каждый круговой маршрут проходит только по указанным в нём станциям и не проходит ни через какую станцию или дорогу дважды.)
A) 18 км Б) 20 км В) 25 км Г) 35 км Д) 50 км
13

Роза хочет вставить отсутствующую плитку в центр квадрата так, чтобы можно было по линиям пройти от левой стрелки до правой. Какая из следующих плиток для этого НЕ подходит?

14
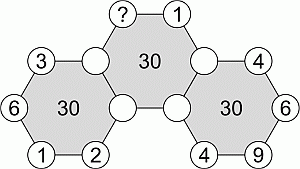
В вершины трёх шестиугольников вписаны числа. Некоторые числа указаны на рисунке, а числа в пустых кружочках скрыты. Сумма шести чисел в вершинах каждого шестиугольника равна 30. Какое число находится в вершине, отмеченной знаком вопроса?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
15
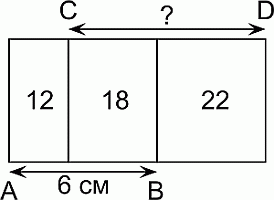
На рисунке изображены три прямоугольника, имеющие общую высоту. Чему равна длина отрезка CD, если известно, что AB = 6 см?
A) 7 см Б) 7,5 см В) 8 см Г) 8,2 см Д) 8,5 см
16

Пирамида на рисунке состоит из 10 шаров одинакового радиуса. На каждом шаре написана одна из букв A, B, C, D или E. Каждой буквой помечено по 2 шара. На рисунке также показаны три вида пирамиды сбоку. Какой буквой помечен шар со знаком вопроса?
A) A Б) B В) C Г) D Д) E
17
У Ромы было четыре белых жетона, а у Вани – четыре серых. Мальчики играли в игру, в которой они по очереди выкладывали по одному из своих жетонов в какую-то из двух стопок. Первым ходил Рома. Какая из следующих пар стопок у них не могла получиться?

18
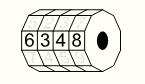
У моего младшего брата есть 4-значный велосипедный замок с цифрами от 0 до 9, записанными по возрастанию на каждом кольце. Он начал с правильной комбинации (открывающей замок) и на всех кольцах сделал одинаковые повороты в одном и том же направлении. В результате он получил комбинацию 6348. Какая из следующих комбинаций не может быть правильной?

19
В коробке находилось 20 яблок и 20 груш. Коля наугад взял 20 фруктов из коробки, а остальные взял Лёша. Какое из следующих утверждений заведомо верно?
A) Коля взял, по крайней мере, одну грушу.
Б) Коля взял столько же яблок, сколько и груш.
В) Коле досталось столько же яблок, сколько и Лёше.
Г) Коля взял столько же груш, сколько яблок взял Лёша.
Д) Коле досталось столько же груш, сколько и Лёше.
20
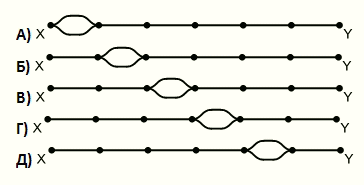
Станции X и Y соединяет единственный железнодорожный путь. Железнодорожная компания хочет одновременно отправлять один поезд из X в Y и один из Y в X. Поезда движутся с постоянными скоростями. Время на дорогу от X до Y составляет 180 минут, а от Y до X – 60 минут. На каком из участков следует построить разъезд, чтобы избежать столкновения?
21
Аня, Боря, Валя, Гена и Дима сидят за круглым столом. Аня сидит не рядом с Борей, Гена рядом с Димой, а Боря – не рядом с Геной. Кто сидит рядом с Валей?
A) Аня и Боря
Б) Боря и Гена
В) Гена и Дима
Г) Дима и Аня
Д) невозможно определить
22
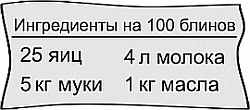
Маша получила у повара рецепт приготовления блинов. У неё есть 6 яиц, 400 г муки, 0,5 л молока и 200 г масла. Какое наибольшее количество блинов Маша сможет приготовить по этому рецепту?
A) 6 Б) 8 В) 10 Г) 12 Д) 15
23

На рисунке показаны три шестерёнки. На каждой имеется по одному чёрному зубу. Как будут расположены чёрные зубья, если меньшая шестерёнка совершит полный оборот?

24
Яблоко и апельсин весят столько же, сколько груша и персик. Яблоко и груша весят меньше апельсина и персика, а груша и апельсин весят меньше яблока и персика. Какой из этих фруктов самый тяжелый?
A) яблоко
Б) апельсин
В) персик
Г) груша
Д) невозможно определить
25

Какое наименьшее количество клеток в квадрате на рисунке нужно ещё закрасить, чтобы полученный рисунок имел 4 оси симметрии?
A) 1 Б) 9 В) 12 Г) 13 Д) 21
26
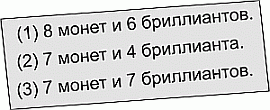
Трёх пиратов спросили, сколько монет и сколько бриллиантов имеет их друг Серая Борода. Каждый из троих ответил правдиво на один из вопросов, но солгал на другой. Их ответы приведены на рисунке. Сколько вместе монет и бриллиантов у Серой Бороды?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
27

На каждой из трёх полок находится по 64 децилитра яблочного сока. Он разлит в бутылки трёх разных размеров: большие, средние и маленькие. Сколько децилитров сока содержится в средней бутылке?
A) 3 Б) 6 В) 8 Г) 10 Д) 14
28
На каждой из шести граней куба со стороной 7 см нарисовали красным фломастером по две диагонали. Затем большой куб разрезали на кубики со стороной 1 см. На скольких маленьких кубиках будет нарисована хотя бы одна красная линия?
A) 54 Б) 62 В) 70 Г) 78 Д) 86
29
Группа состоит из 10 мифических существ – эльфов и троллей. Каждому из них выдали жетон с одним из чисел от 1 до 10, всем с разными числами. Затем у каждого из них спросили, какое число на его жетоне. Каждый назвал число от 1 до 10. Сумма названных чисел оказалась равна 36. При этом каждый тролль соврал, а каждый эльф сказал правду. Какое наименьшее количество троллей могло быть в этой группе?
A) 1 Б) 3 В) 4 Г) 5 Д) 7
30
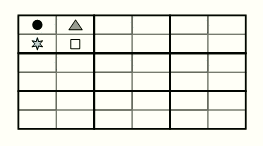
Прямоугольные карточки разделены на четыре равные ячейки, в которых нарисованы четыре разные фигурки. Из карточек можно сложить прямоугольник так, что соседние карточки будут соприкасаться друг с другом ячейками с одинаковыми фигурками. Одна из карточек этого прямоугольника показана на рисунке. Какой из следующих карточек заведомо НЕ может быть в таком прямоугольнике?
