1
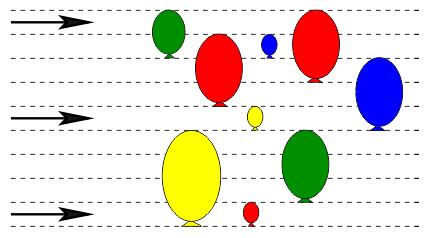
На рисунке показаны летящие стрелы и неподвижные шары. Когда стрела попадает в шар, шар лопается, а стрела летит дальше. Сколько всего шаров останутся целыми?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
2
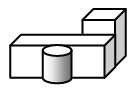
На столе лежат три предмета (см. рис.). Петя посмотрел на них сверху. Что он увидел?

3
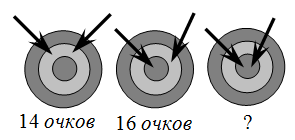
Диана бросает дротики в мишень. Первый раз она набрала 14 очков, второй раз 16. Сколько очков она набрала в третий раз?
A) 17 Б) 18 В) 19 Г) 20 Д) 22
4
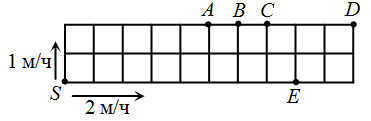
Сад разделён на квадраты. Две улитки начинают ползти из точки S в разных направлениях по периметру сада со скоростями 1 м/ч и 2 м/ч. В какой точке они встретятся?
A) A Б) B В) C Г) D Д) E
5

Алиса правильно выполнила на клетчатой бумаге вычитание двух двузначных чисел. Затем две клетки она закрасила красным фломастером (см. рис.). Чему равна сумма цифр в закрашенных клетках?
A) 8 Б) 9 В) 12 Г) 13 Д) 15
6
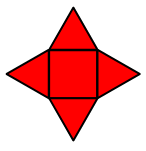
Звезда состоит из квадрата и четырёх равносторонних треугольников. Периметр квадрата равен 36. Чему равен периметр звезды?
A) 144 см Б) 120 см В) 104 см Г) 80 см Д) 72 см
7
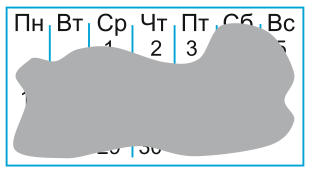
На рисунке показан календарь некоторого месяца. К сожалению, большая его часть залита чернилами. Какой день недели был 25 числа этого месяца?
A) понедельник Б) вторник В) среда Г) суббота Д) воскресенье
8
Какое наименьшее число раз нужно подбросить игральный кубик, чтобы быть уверенным, что какой-то результат повторится?
A) 5 Б) 6 В) 7 Г) 12 Д) 18
9
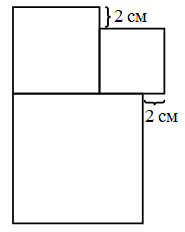
На рисунке изображены три квадрата. Сторона наименьшего из них равна 6 см. Чему равна сторона наибольшего квадрата?
A) 8 см Б) 10 см В) 12 см Г) 14 см Д) 16 см
10
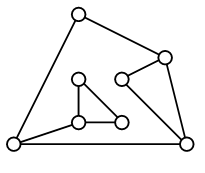
На рисунке кружочками изображены лампочки, некоторые из них соединены проводами. Будем называть две лампочки, соединённые проводом, соседними. Первоначально все лампочки выключены. Если прикоснуться к какой-то из лампочек, то она и все соседние с ней лапочки зажигаются. К какому наименьшему числу лампочек нужно прикоснуться, чтобы зажглись все лампочки?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
11
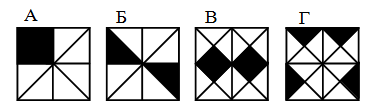
В каком из квадратов площадь чёрной части наибольшая?
A) A Б) Б В) В Г) Г Д) такого квадрата нет
12
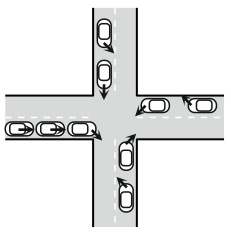
9 автомобилей подъехали к перекрёстку и собираются пересечь его так, как указывают стрелки. На каком рисунке показано, как автомобили покинули перекрёсток?

13
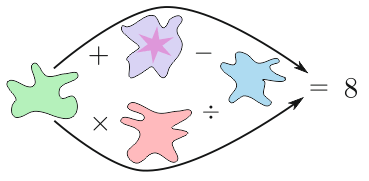
Каждое из пятен закрывает какую-то одну из цифр 1, 2, 3, 4 или 5. Известно, что оба вычисления, указанные стрелками, являются правильными. Какое число закрыто пятном со звездой?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
14
В одной из трёх комнат скрывается лев. На двери первой комнаты написано: «Лев не здесь», на двери второй комнаты: «Лев здесь», а на двери третьей комнаты: «2 + 3 = 5». Только одна из надписей является правдивой. В какой комнате скрывается лев?
A) в первой
Б) во второй
В) в третьей
Г) в первой или второй
Д) в любой
15
Две девочки – Ева и Оля – и три мальчика – Адам, Иван и Степан – играют с мячом. Когда у девочки есть мяч, она бросает его другой девочке или мальчику. Когда у мальчика есть мяч, он бросает его другому мальчику, но не тому, от которого он его только что получил. Ева начинает, бросая мяч Адаму. Кто сделает пятый бросок?
A) Адам Б) Ева В) Иван Г) Ольга Д) Степан
16
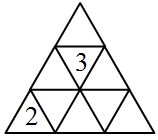
Эмили хочет вписать числа в ячейки треугольной таблицы так, чтобы суммы чисел в любых двух соседних по стороне ячейках были одинаковы. Два числа она уже вписала так, как показано на рисунке. Какой может быть сумма всех чисел в таблице?
A) 18 Б) 20 В) 21 Г) 22 Д) невозможно определить
17
В понедельник Александра отправила свою фотографию пяти своим друзьям. Далее, каждый следующий день любой, кто получил фотографию Александры, на следующий день после получения отправил её ровно двум своим друзьям, которые её ещё не получали. В какой день недели число абонентов, получивших фотографию Александры, станет больше 100?
A) в среду
Б) в четверг
В) в пятницу
Г) в субботу
Д) в воскресенье
18
Грани куба окрашены в белый, серый и чёрный цвет так, что противоположные грани имеют разные цвета. Какая из следующих развёрток не может быть развёрткой поверхности этого куба?

19
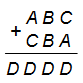
В примере на сложение цифры заменили буквами (одинаковые цифры одинаковыми буквами, а разные – разными). Какую цифру заменили буквой B?
A) 0 Б) 2 В) 4 Г) 5 Д) 6
20
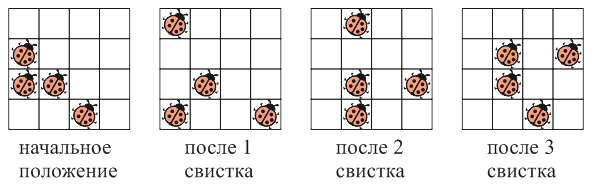
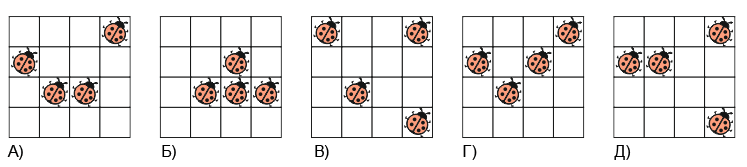
Четыре божьи коровки сидят в разных клетках доски 4 × 4. Одна из них спит и не двигается. Остальные 3 божьи коровки каждый раз, когда Вася свистнет, переползают в соседние по стороне клетки. Они могут двигаться вверх, вниз, вправо или влево, но не могут возвращаться в клетки, в которых они только что были. Как могут располагаться божьи коровки после четвёртого свистка?
21
Даны семь чисел: 3, 5, 2, 6, 1, 4, 7. Маша выбирает из них три числа, сумма которых равна 8. А Даша из этих же чисел выбирает три числа, сумма которых равна 7. Сколько одинаковых чисел выбрали обе девочки?
A) 0 Б) 1 В) 2 Г) 3 Д) невозможно определить
22

Пять шаров имеют массы 30, 50, 50, 50 и 80 г. На рисунке показаны три взвешивания на чашечных весах. Какой шар имеет массу 30 г?
A) A Б) B В) C Г) D Д) E
23
Если A, B и C – три различные цифры, то наибольшее возможное шестизначное число, записанное с помощью трёх цифр A, двух цифр B и одной цифры C не может равняться…
A) AAABBC Б) CAAABB В) BBAAAC Г) AAABCB Д) AAACBB
24
Кате и её маме вместе 36 лет, а её маме и её бабушке – 81 год. Сколько лет было бабушке, когда Катя родилась?
A) 28 Б) 38 В) 45 Г) 53 Д) 56
25
Коля хочет разбить числа 2, 3, 4, …, 10 на несколько групп так, чтобы суммы чисел во всех группах были одинаковы. Какое наибольшее количество групп у него может получиться?
A) 2 Б) 3 В) 4 Г) 5 Д) другой ответ
26
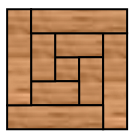
Петя распилил доску со стороной 8 см параллельно этой стороне на 9 частей: 1 квадрат и 8 прямоугольников. Затем он сложил все полученные части так, что получился квадрат (см. рис.). Чему была равна длина доски?
A) 150 см Б) 168 см В) 196 см Г) 200 см Д) 232 см
27

В клетки таблицы 5 × 5 вписаны числа 0 и 1 так, что в любом квадрате 2 × 2 есть ровно три одинаковых числа. Какое наибольшее значение может иметь сумма всех чисел в таблице?
A) 22 Б) 21 В) 20 Г) 19 Д) 18
28
За круглым столом сидят 14 человек: лжецов и правдивых. Каждый из них сказал: «Оба мои соседа слева и справа – лжецы». Какое наибольшее число лжецов может быть за этим столом?
A) 7 Б) 8 В) 9 Г) 10 Д) 14
29
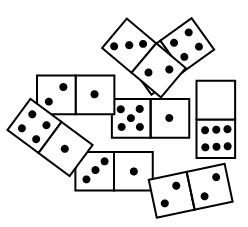
На столе лежат 8 плиток домино (см. рис.). У одной из плиток одна клетка скрыта. Известно, что из всех этих домино можно сложить квадрат 4 × 4 так, что количества точек во всех строчках и всех столбцах будут одинаковы. Сколько точек на скрытой клетке?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
30
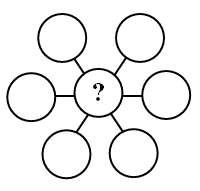
Числа 3, 4, 5, 6, 7, 8 и 9 надо вписать в кружочки на диаграмме так, чтобы суммы чисел во всех тройках кружочков, лежащих на одной прямой, были одинаковы. Какие из этих чисел могут оказаться в центральном кружочке? Выберите ответ, где указана их сумма.
A) 3 Б) 6 В) 9 Г) 12 Д) 18