1

Пчёлка Бззз хочет перелететь на цветок. Какую из следующих последовательностей перелётов ей нужно совершить?

2
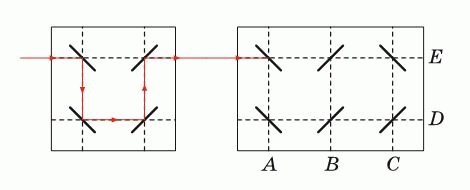
Луч лазера отражается от зеркал так, как показано на первом рисунке. В какой точке выйдет луч лазера на втором рисунке?
A) A Б) B В) C Г) D Д) E
3
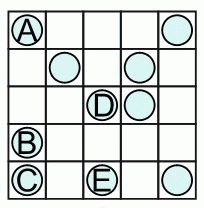
Раиса хочет, чтобы в каждой строчке и в каждом столбце следующей клетчатой доски лежало ровно 2 монеты. Какую монету ей нужно переместить в пустую клетку?
A) A Б) B В) C Г) D Д) E
4
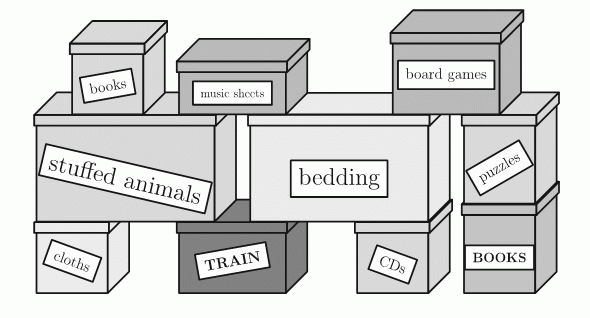
Какое наименьшее количество вышестоящих коробок нужно убрать, чтобы можно было открыть коробку с надписью «TRAIN»?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
5
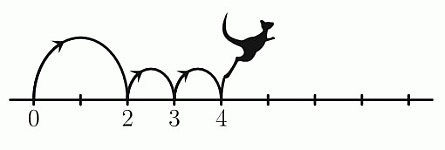
Кенгуру прыгает по прямой и делает один длинный прыжок после двух коротких, как показано на рисунке. Кенгуру начал прыгать с отметки 0 и закончил на отметке 16. Сколько прыжков он сделал?
A) 6 Б) 8 В) 10 Г) 11 Д) 12
6
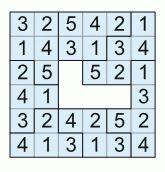
Аня хочет сложить квадрат так, чтобы в любых соседних по стороне клетках были записаны разные числа. Каким из недостающих фрагментов ей нужно воспользоваться?

7
Дано равенство:
2022 + ☐ = 2020 + ☐.
Какие из следующих чисел должны быть вписаны вместо квадратиков, чтобы оно стало правильным?
A) 3 и 5
Б) 4 и 1
В) 3 и 4
Г) 7 и 2
Д) 9 и 8
8
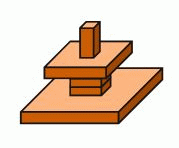
Женя построил башню, показанную на рисунке справа. Как выглядит башня, если на неё смотреть сверху?

9

Пять автомобилей движутся в одном направлении. Сначала автомобиль 5 обогнал два автомобиля. Затем автомобиль 3 обогнал два впереди идущих автомобиля. После этого автомобиль 2 обогнал два впереди идущих автомобиля. В каком порядке движутся автомобили в результате?
A) 1, 2, 3, 5, 4
Б) 2, 1, 3, 5, 4
В) 2, 1, 5, 3, 4
Г) 3, 1, 4, 2, 5
Д) 4, 1, 2, 5, 3
10
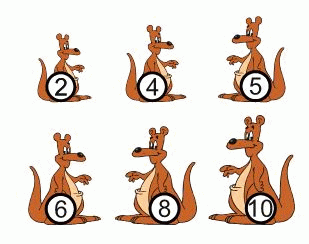
Возрасты шести кенгуру: 2, 4, 5, 6, 8 и 10 лет. Сумма лет четырёх из них равна 22 года. Сколько лет двум остальным кенгуру?
A) 2 и 8
Б) 4 и 5
В) 5 и 8
Г) 6 и 8
Д) 6 и 10
11
Во время каникул я отправил своим друзьям пять открыток, показанных ниже. На открытке Мише нет уток. На открытке Кате есть солнце. На открытке Полине ровно два живых существа. На открытке Люсе изображена собака. На открытке Вите изображены кенгуру. Какую открытку получил Миша?

12
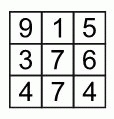
Миша хотел, заполнить клетки таблицы числами так, чтобы суммы чисел во всех строчках и столбцах были одинаковыми. Но он сделал одну ошибку. Какое число он должен исправить?
A) 1 Б) 3 В) 4 Г) 5 Д) 7
13
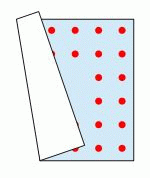
У Аладдина квадратный ковер. Вдоль каждой стороны ковра в две линии расположены одинаковые количества точек. К несчастью, ковёр завернулся как показано на рисунке. Сколько всего точек на ковре?
A) 48 Б) 44 В) 40 Г) 36 Д) 32
14
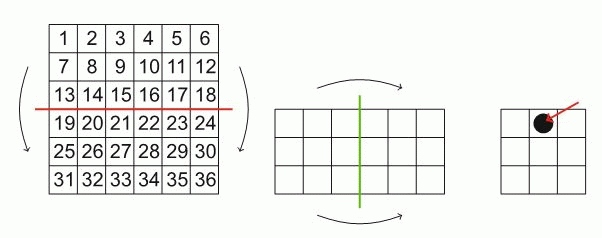
Жанна согнула квадрат с числами дважды, как показано на рисунке. Затем она проткнула сложенный квадрат в указанной точке. Какие числа записаны в клетках, которые она проткнула?
A) 8, 11, 26, 29
Б) 14, 17, 20, 23
В) 15, 16, 21, 22
Г) 14, 16, 21, 23
Д) 15, 17, 20, 22
15
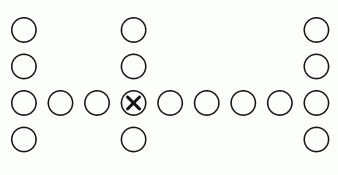
Учащиеся в классе сидят рядами. В каждом ряду одинаковое количество учеников. Перед Робертом 2 ряда учеников, а позади него – 1 ряд учеников. В его ряду 3 ученика слева от него и 5 учеников справа. Сколько учеников в этом классе?
A) 10 Б) 17 В) 18 Г) 27 Д) 36
16
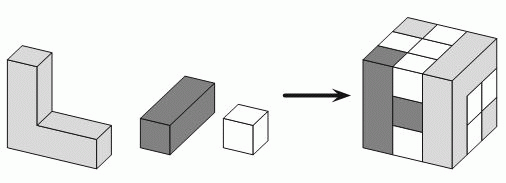
Куб построен из блоков трёх видов (см. рис.). Сколько белых блоков было при этом использовано?
A) 8 Б) 11 В) 13 Г) 16 Д) 19
17
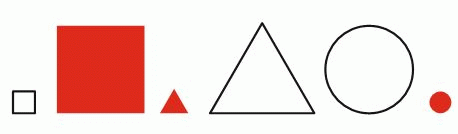
Ванда решила выбрать несколько из следующих фигур. Она хочет, чтобы среди них были 2 окрашенные фигуры, 2 большие и 2 круглые. Какое наименьшее число фигур она может выбрать, чтобы все эти условия были выполнены?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
18
В турнире по футболу участвуют 3 команды. Каждая команда должна сыграть с каждой другой один матч. За выигрыш в матче команда получает 3 очка, за ничью – 1 очко, а за проигрыш – ни одного очка. Какое из следующих чисел НЕ МОГЛО быть числом очков ни у одной из команд после завершения турнира?
A) 1 Б) 2 В) 4 Г) 5 Д) 6
19
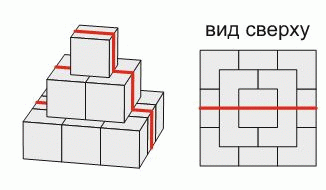
Пирамида построена из кубиков с ребром 10 см. Муравей переползает через пирамиду по красной линии, изображенной на рисунке. Какую длину имеет данный путь муравья?
A) 30 см Б) 60 см В) 70 см Г) 80 см Д) 90 см
20
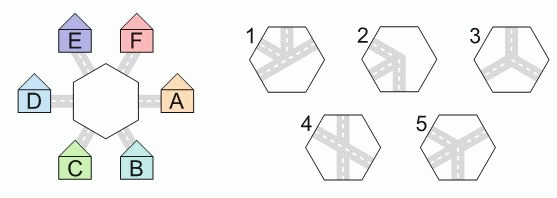
Аня хочет вложить в центр между домиками одну из плиток, указанных на рисунке справа. Она хочет при этом, чтобы от домика A можно было пройти по дорожкам к домикам B и E, но нельзя было пройти к D. Какую из плиток ей нужно выбрать. Плитки можно поворачивать.
A) 1 или 2
Б) 2 или 3
В) 1 или 4
Г) 4 или 5
Д) 1 или 5
21
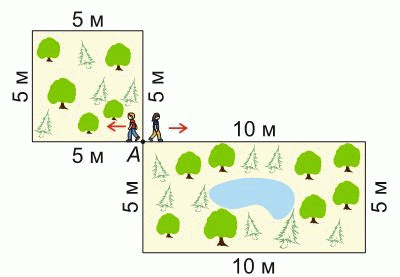
Лёша и Серёжа начинают идти из точки А вокруг квадратного и прямоугольного парков, соответственно, в указанных направлениях с одинаковой скоростью. Через некоторое время они снова встретились в точке А. Сколько раз обошёл вокруг квадратного парка Лёша до этой встречи?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
22
Пятеро девочек ели сливы. Лена съела на 2 сливы больше, чем Соня. Варя съела на 3 сливы меньше, чем Лена. Катя съела на 1 сливу больше, чем Варя, но на 3 сливы меньше, чем Алиса. Какие две девочки съели одинаковое количество слив?
A) Катя и Лена
Б) Катя и Соня
В) Лена и Алиса
Г) Соня и Алиса
Д) Алиса и Варя
23

Маленькая «гусеница» на рисунке свернулась, чтобы заснуть. Как теперь она может выглядеть?

24
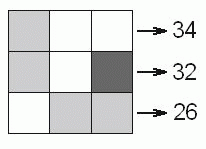
Под клетками одного и того же цвета скрыты одинаковые числа так, что суммы чисел в строчках такие, как показано на рисунке. Какое число скрыто под чёрной клеткой?
A) 6 Б) 8 В) 10 Г) 12 Д) 14