1
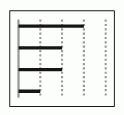
Диаграмма показывает, сколько времени на прошлой неделе Генрих пользовался приложениями, установленными на его смартфоне. На этой неделе на два приложения он потратил столько же времени, а на два другие – в два раза меньше. Как НЕ МОЖЕТ выглядеть соответствующая диаграмма?

2
Сколько трёхзначных натуральных чисел делятся на 13?
A) 68 Б) 69 В) 70 Г) 76 Д) 77
3
Белла старше Чарли, но моложе Лили. Тедди старше Беллы. У кого из них может быть одинаковый возраст?
A) у Чарли и Тедди
Б) у Тедди и Лили
В) у Лили и Чарли
Г) у Беллы и Лили
Д) у Тедди и Беллы
4
Произведение цифр 10-значного числа равно 15. Чему равна сумма цифр этого числа?
A) 8 Б) 12 В) 15 Г) 16 Д) 20
5
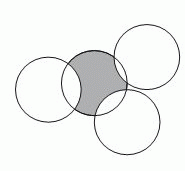
Четыре круга радиуса 1 пересекаются, как показано на рисунке. Чему равен периметр окрашенной фигуры?
A) π
Б) числу между π и 1,5π
В) 1,5π
Г) 2π
Д) π2
6
Давид выписывает в порядке возрастания все числа от 2 до 2022, в записи которых нет других цифр, кроме 0 и 2. Какое число окажется ровно посередине в таком списке?
A) 200 Б) 220 В) 222 Г) 2000 Д) 2022
7
Сколько действительных корней имеет уравнение
(x − 2)2 + (x + 2)2 = 0?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
8
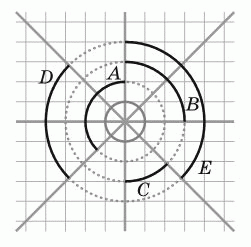
Четыре прямые пересекаются в одной точке и образуют восемь равных углов. Какая из чёрных дуг имеет такую же длину, как серая окружность в центре?
A) A Б) B В) C Г) D Д) E
9
Пусть a, b и c – ненулевые числа. Известно, что числа −2a4b3c2 и 3a3b5c-4 имеют один и тот же знак. Какое из следующих утверждение верно?
A) ab > 0
Б) b < 0
В) c > 0
Г) bc > 0
Д) a < 0
10

Миша отметил четыре точки на прямой так, как показано на рисунке. Известно, что AC = 12 cм, BD = 18 cм. Каково расстояние между серединами отрезков AB и CD?
A) 15 см Б) 12 см В) 18 см Г) 6 см Д) 9 см
11
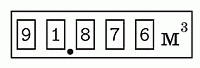
Толя заметил, что на счётчике воды в его квартире все цифры различные (см. рис.). Сколько воды должно быть использовано до ближайшего момента, когда снова на счётчике все цифры будут различными?
A) 0,006 м3 Б) 0,034 м3 В) 0,086 м3 Г) 0,137 м3 Д) 1,048 м3
12
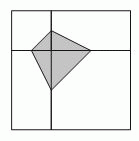
Квадрат разбили на два меньших неравных квадрата и два прямоугольника, как показано на рисунке. Вершины окрашенного четырёхугольника являются серединами соответствующих сторон полученных квадратов. Площадь этого четырёхугольника равна 3. Чему равна площадь неокрашенной части исходного квадрата?
A) 12 Б) 15 В) 18 Г) 21 Д) 24
13
Чему равен наибольший общий делитель чисел 22021 + 22022 и 32021 + 32022?
A) 22021 Б) 1 В) 2 Г) 6 Д) 12
14
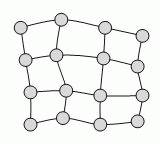
16 городов соединены дорогами так, как показано на рисунке. Правительство хочет построить электростанции в некоторых из этих городов. Каждая электростанция должна обеспечить электроэнергией город, в котором она расположена, и другие города, связанные с данным городом одной дорогой. Какое наименьшее количество электростанций нужно построить, чтобы все города были обеспечены электроэнергией?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
15
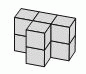
Из каких двух фигур в вариантах ответа можно сложить фигуру на рисунке сверху?

16
В турнире участвуют 8 игроков. Марта знает, что победит всех, кроме Эллы, которая самая сильная и победит всех. В первом туре игроки случайным образом разбиваются на четыре пары. Победитель каждого матча проходит во второй тур, в котором снова пары формируются случайным образом. Победители второго тура выходят в финал. Какова вероятность того, что Марта не пройдёт в финал?
A) 1 Б) 1/2 В) 2/7 Г) 3/7 Д) 4/7
17
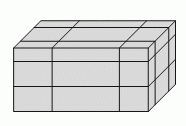
Прямоугольный параллелепипед плоскостями, параллельными граням, разбит на 27 меньших параллелепипедов, как показано на рисунке. Площадь поверхности данного параллелепипеда равна S. Чему равна сумма поверхностей всех 27 полученных параллелепипедов?
A) 2S Б) 2,5S В) 3S Г) 4S Д) другой ответ
18
Среднее арифметическое пяти чисел равно 24. Среднее арифметическое трёх наименьших из них равно 19, а трёх наибольших – 28. Чему равно среднее по величине число?
A) 20 Б) 21 В) 22 Г) 23 Д) 24
19
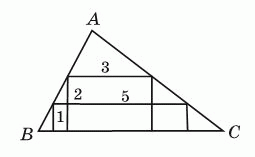
Два прямоугольника 1 × 5 и 2 × 3 вписаны в треугольник ABC так, как показано на рисунке. Чему равна высота данного треугольника, опущенная на сторону BC?
A) 3
Б) 3,5
В) 8/3
Г) 16/5
Д) другой ответ
20
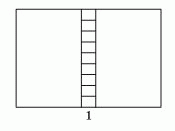
Прямоугольник на рисунке разбит на 11 меньших прямоугольников, подобных исходному. Ориентация самых маленьких прямоугольников такая же как у исходного прямоугольника. Большая сторона одного из самых маленьких прямоугольников равна 1. Чему равен периметр исходного прямоугольника?
A) 20 Б) 24 В) 27 Г) 30 Д) 36
21
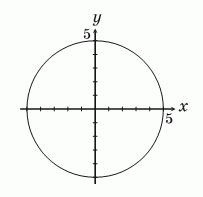
Окружность с центром в начале координат имеет радиус 5. Сколько всего на этой окружности точек, у которых обе координаты являются целыми числами?
A) 5 Б) 8 В) 12 Г) 16 Д) 20
22
Сколько существует трёхзначных натуральных чисел, которые в 5 раз больше произведения их цифр?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
23
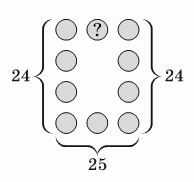
В кружочки на рисунке вписаны числа от 1 до 10 (каждое ровно один раз). Суммы чисел в левом и в правом столбцах равны 24. Сумма чисел в нижней строке равна 25. Чему равно число в кружочке, отмеченном знаком вопроса?
A) 2
Б) 4
В) 5
Г) 6
Д) ни одно из предыдущих
24
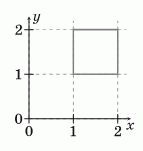
Квадрат со стороной 1 расположен на координатной плоскости так, как показано на рисунке. Каждую его точку (x, y) заменили на точку 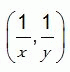 .
.
Какая фигура в результате получилась?

25
Вершины 20-угольника пронумерованы числами от 1 до 20 так, что номера соседних вершин отличаются только на 1 или на 2. Стороны, вершины на концах которых отличаются на 1, окрасили в красный цвет. Сколько красных сторон могло получиться?
A) 1
Б) 2
В) 5
Г) 10
Д) имеется несколько различных возможностей
26
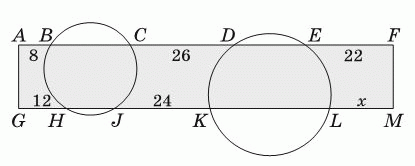
Две окружности пересекают прямоугольник AFMG так, как показано на рисунке. Известно, что AB = 8, CD = 26, EF = 22, GH = 12 и JK = 24. Какую длину имеет отрезок LM?
A) 14 Б) 15 В) 16 Г) 17 Д) 18
27
Пусть N – натуральное число. Сколько натуральных чисел на числовой прямой находится между числами
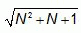 и
и 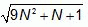 ?
?
A) N + 1
Б) 2N – 1
В) 2N
Г) 2N + 1
Д) 3N
28
В последовательности an: 0 < a1 < 1 и a2n = a2an + 1, a2n + 1 = a2an – 2 для всех n ≥ 1. Известно, что a7 = 2. Чему равно значение a2?
A) a1 Б) 2 В) 3 Г) 4 Д) 5
29
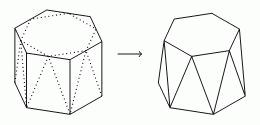
Верхние углы правильной шестиугольной призмы срезали, как показано на рисунке. Верхняя грань стала меньшим правильным шестиугольником, а 6 боковых прямоугольных граней преобразовались в 12 равнобедренных треугольников двух разных размеров. На какую часть уменьшился объём призмы?
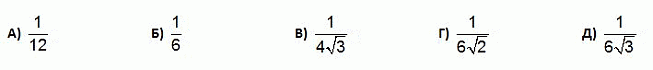
30
Футбольный матч между командами Северного Берракана и Южного Берракана проходит на стадионе с прямоугольной трибуной для зрителей. В каждом ряду кресел сидят 11 фанатов Северного Берракана, а в каждом столбце трибуны – 14 фанатов Южного Берракана. 17 мест оказались пустыми. Какое наименьшее количество мест может быть на зрительской площадке стадиона?
A) 500 Б) 660 В) 690 Г) 840 Д) 994