1
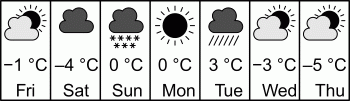
Павел просматривает приложение «Погода», которое показывает прогнозируемую погоду и максимальную температуру на ближайшие семь дней. В каком из следующих ответов приведён график максимальной температуры данного на рисунке прогноза?

2
Сколько целых чисел находится в интервале
(20 – √21; 20 + √21)?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
3
Куб с ребром 1 разрезали на два одинаковых параллелепипеда. Чему равна площадь поверхности одного такого параллелепипеда?
A) 1,5 Б) 2 В) 3 Г) 4 Д) 5
4
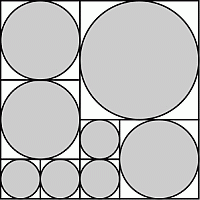
Большой квадрат разбит на меньшие квадраты так, как показано на рисунке. В каждый из этих квадратов вписали серый круг. Какая часть площади большого квадрата закрашена серым цветом?
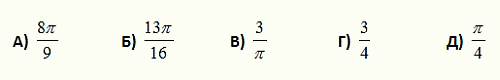
5
После шторма прошлой ночью флагшток (вертикальный шест, на котором крепится флаг) на здании нашей школы наклонился. Если смотреть с северо-запада, его вершина находится справа от его нижней точки. Если смотреть с востока, то его вершина тоже будет правее его нижней точки. В каком из следующих направлений мог наклониться флагшток?

6
Прямоугольный лист бумаги имеет длину x и ширину y, где x > y. Лист можно свернуть двумя способами так, чтобы получилась боковая поверхность цилиндра. Чему равно отношение объёма более длинного цилиндра к объёму более короткого цилиндра?
A) y2 : x2
Б) y : x
В) 1 : 1
Г) x : y
Д) x2 : y2
7
Пусть х = π/4. Какое из следующих чисел наибольшее?
A) x4
Б) x2
В) x
Г) √x
Д) 4√x
8
Сколько всего существует кратных 3 трёхзначных чисел, в записи которых участвуют только цифры 1, 3 и 5? (Одну и ту же цифру можно использовать несколько раз).
A) 3 Б) 6 В) 9 Г) 18 Д) 27
9
Чему равна площадь треугольника на координатной плоскости с вершинами в точках (p; q), (3p; q) и (2p; 3q), где p, q > 0?
A) pq /2 Б) pq В) 2pq Г) 3pq Д) 4pq
10
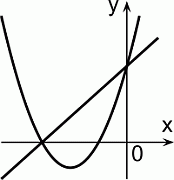
Парабола на рисунке имеет уравнение y = ax2 + bx + c при некоторых a, b и c. Какое из следующих уравнений может иметь прямая на рисунке?
A) y = bx + c
Б) y = cx + b
В) y = ax + b
Г) y = ax + c
Д) y = cx + a
11
Какую часть составляют нечётные делители числа 7! среди всех его делителей? (Запись n! обозначает произведение всех натуральных чисел от 1 до n.)
A) 1/2 Б) 1/3 В) 1/4 Г) 1/5 Д) 1/6
12
Если A = (0; 1) ∪ (2; 3) и B = (1; 2) ∪ (3; 4), то чему равно множество всех чисел вида a + b, где a ∈ A, b ∈ B?
A) (1; 7)
Б) (1; 5) ∪ (5; 7)
В) (1; 3) ∪ (3; 7)
Г) (1; 3) ∪ (3; 5) ∪ (5; 7)
Д) другой ответ
13
Сколько трёхзначных натуральных чисел обладает свойством: если цифры числа записать в обратном порядке, то получится число, на 99 большее исходного?
A) 8 Б) 64 В) 72 Г) 80 Д) 81
14
Первые 1000 натуральных чисел записали в некотором порядке. Затем в каждой тройке подряд стоящих чисел вычислили их сумму. Какое наибольшее количество нечётных сумм могло получиться?
A) 997 Б) 996 В) 995 Г) 994 Д) 993
15
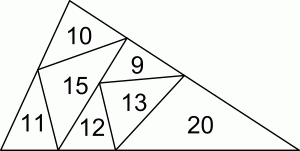
Треугольник разрезали на меньшие треугольники так, как показано на рисунке. Число внутри каждого меньшего треугольника указывает его периметр. Чему равен периметр исходного треугольника?
A) 31 Б) 34 В) 41 Г) 62 Д) другому числу
16
Обозначим через p(N) произведение цифр числа N. Например, p(23) = 2 • 3 = 6. Чему равна сумма
p(10) + p(11) + p(12) + … + p(99) + p(100)?
A) 2025 Б) 4500 В) 5005 Г) 5050 Д) другому числу
17
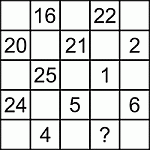
В каждую клетку квадрата 5 × 5 записано целое число. Некоторые из чисел показаны на рисунке, а некоторые скрыты. При этом, суммы чисел, стоящих во всех строчках и столбцах одинаковы. Какое число записано в клетке, отмеченной вопросительным знаком?
A) 8 Б) 10 В) 12 Г) 18 Д) 23
18
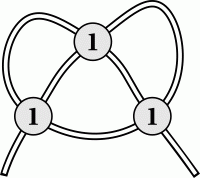
На столе лежит верёвка, частично закрытая тремя монетами, как показано на рисунке. Под каждой монетой верёвка может выглядеть как 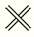 или
или  с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?
с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?
A) 1/2 Б) 1/4 В) 1/8 Г) 3/4 Д) 3/8
19

Вредный щенок схватил конец рулона бумаги и начал его тянуть с постоянной скоростью. Какой из приведённых ниже графиков функции лучше всего описывает толщину y рулона в зависимости от длины x развёрнутой части?

20
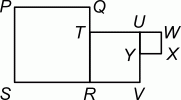
На рисунке изображены три квадрата: PQRS, TRVU и UWXY. Точки P, T и X лежат на одной прямой. Площадь квадрата PQRS равна 36, а площадь TRVU равна 16. Чему равна площадь треугольника PXV?
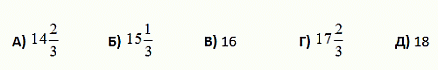
21
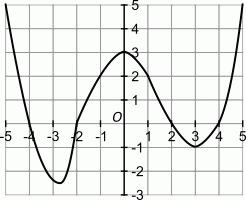
На рисунке изображён график функции f: [–5; 5] → 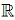 . Сколько различных решений имеет уравнение f(f(x)) = 0?
. Сколько различных решений имеет уравнение f(f(x)) = 0?
A) 2 Б) 4 В) 6 Г) 7 Д) 8
22
На доске были записаны числа 1, 2, 7, 9, 10, 15 и 19. Двое игроков по очереди стирали по одному числу, пока на доске не осталось только одно число. Сумма чисел, удалённых одним из игроков, оказалась в два раза больше суммы чисел, удалённых другим игроком. Какое число осталось?
A) 7 Б) 9 В) 10 Г) 15 Д) 19
23
Функция f(x) такова, что f(1) = 2 и для любых x и y верно равенство f(x + y) = f(x) • f(y). Чему равно значение
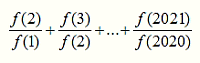 ?
?
A) 0 Б) 2021 В) 2 Г) 2020 Д) другому числу
24
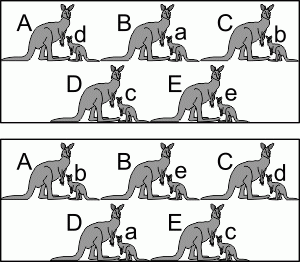
У пяти кенгуру с именами A, B, C, D и E есть по одному ребенку с именами a, b, c, d и e. На первом групповом фото ровно двое кенгурят стоят рядом со своими мамами. На втором фото ровно трое кенгурят стоят рядом со своими мамами. Чьим ребенком является кенгурёнок а?
A) A Б) B В) C Г) D Д) E
25
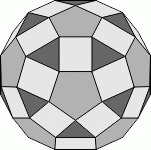
Многогранник на рисунке имеет 12 правильных пятиугольных граней, а остальные грани – либо равносторонние треугольники, либо квадраты. Каждая пятиугольная грань окружена пятью квадратными гранями, а каждая треугольная грань окружена тремя квадратными гранями. Ваня записал число 1 на каждой треугольной грани, число 5 на каждой пятиугольной грани и число -1 на каждой квадратной грани. Чему равна сумма чисел на всех гранях данного многогранника?
A) 20 Б) 50 В) 60 Г) 80 Д) 120
26
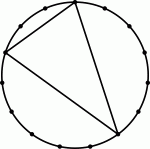
На окружности через равные промежутки отмечено 15 точек. Сколько существует попарно не равных треугольников с вершинами в этих точках?
A) 19 Б) 91 В) 46 Г) 455 Д) 23
27
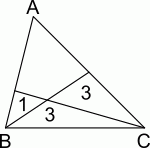
Треугольник ABC разбит на четыре части двумя отрезками, как показано на рисунке. Площади треугольных частей равны 1, 3 и 3. Чему равна площадь исходного треугольника?
A) 12 Б) 12.5 В) 13 Г) 13.5 Д) 14
28
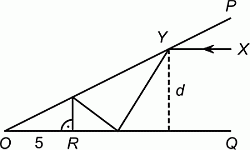
Два плоских зеркала OP и OQ наклонены под острым углом (см. рис.). Луч света XY, параллельный QO, падает на зеркало OP в точке Y. После этого он отражается и попадает на зеркало OQ, повторно отражается и снова попадает на зеркало OP. После третьего отражения луч попадает под прямым углом на зеркало OQ в точку R. Известно, что OR = 5. На каком расстоянии d от зеркала OQ находится точка Y?
A) 4 Б) 4.5 В) 5 Г) 5.5 Д) 6
29
Пусть M(k) – максимальное значение выражения |4x2 – 4x + k| при x ϵ [–1; 1], где k –произвольное действительное число. Чему равно наименьшее возможное значение M(k)?
A) 4 Б) 9/2 В) 5 Г) 11/2 Д) 8
30
В некоторой игре, чтобы выиграть, нужно опередить другого игрока на 3 очка. Два игрока A и B играют в такую игру и в некоторый момент игрок A опережает игрока В на 1 очко. Игроки имеют одинаковую вероятность выиграть каждое следующее очко. Какова вероятность того, что А выиграет игру?
A) 1/2 Б) 2/3 В) 3/4 Г) 4/5 Д) 5/6