1
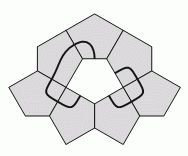
Фигура на рисунке состоит из пятиугольных плиток одинакового размера. Какую плитку нужно поместить в центр данной фигуры, чтобы на её поверхности получилась самопересекающаяся петля?

2
Какое из следующих чисел на 2 меньше числа, кратного 10, на 2 больше квадрата натурального числа и в 2 раза больше простого числа?
A) 78 Б) 58 В) 38 Г) 18 Д) 4
3
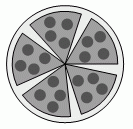
Кенгурёнок разрезал пиццу на шесть равных частей. Он съел одну часть, а затем равномерно раздвинул остальные части так, чтобы края соседних частей образовали одинаковые углы. Чему равна величина одного такого угла?
A) 5° Б) 8° В) 9° Г) 10° Д) 12°
4
У Васи необычная привычка рисовать координатную плоскость Оxy с осями, направленными влево и вниз. Как будет выглядеть график функции y = x + 1 в координатной системе Васи?

5
У Кати неправильный игральный кубик. Вероятность выпадения 2, 3, 4, 5 по-прежнему равна 1/6, как у обычного кубика. Но вероятность выпадения 6 в два раза больше вероятности выпадения 1. Какова вероятность выпадения 6?
A) 1/4 Б) 1/6 В) 7/36 Г) 2/9 Д) 5/18
6
Какое из следующих выражений имеет такое же значение, как выражение
1615 + 1615 + 1615 + 1615 ?
A) 1619
Б) 431
В) 460
Г) 1660
Д) 4122
7
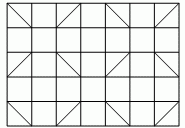
Бобёр хочет раскрасить квадраты и треугольники на рисунке так, чтобы никакие два из них не были окрашены в один цвет, если они имеют хотя бы одну общую точку. Какое наименьшее количество различных красок для этого понадобится?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
8
На столе стоят 6 стаканов открытой стороной вверх. За один ход можно перевернуть любые 4 из них. Какое наименьшее число ходов нужно сделать, чтобы перевернуть все стаканы?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
9
Степан выполняет следующие действия. Он начинает с числа 1 и умножает его либо на 6, либо на 10. Затем полученный результат он снова умножает либо на 6, либо на 10 и так далее много раз. Какое из следующих чисел он не может получить?
A) 2100 ∙ 320 ∙ 580
Б) 290 ∙ 320 ∙ 580
В) 290 ∙ 320 ∙ 570
Г) 2110 ∙ 380 ∙ 530
Д) 250 ∙ 550
10
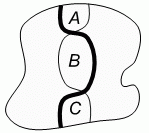
Широкая и узкая тропинки в парке пересекаются, как показано на рисунке. Каждая тропинка делит парк на две части равной площади. Какое из следующих равенств заведомо верно для площадей A, B и C?
A) A = C
Б) B = A + C
В) B = 1/2(A + C)
Г) B = 2/3(A + C)
Д) B = 3/5(A + C)
11
Ровно одно из следующих утверждений об определённом натуральном числе n верно. Какое?
A) n делится на 3
Б) n делится на 6
В) n – нечётное
Г) n = 2
Д) n – простое
12
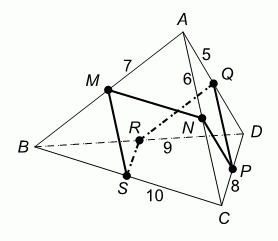
Длины рёбер треугольной пирамиды ABCD равны 5, 6, 5, 8, 9 и 10, как показано на рисунке. Точки M, N, P, Q, R и S – середины соответствующих рёбер. Какую длину имеет замкнутая 6-звенная ломаная MNPQRSM?
A) 19 Б) 20 В) 21 Г) 22 Д) 23
13
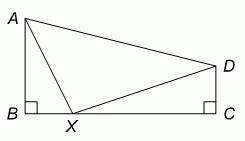
В четырёхугольнике ABCD углы при вершинах B и C – прямые, AB = 4, BC = 8, CD = 2, точка X лежит на стороне BC. Какое наименьшее значение может иметь сумма AX + XD?
A) 9√2
Б) 12
В) 13
Г) 10
Д) другой ответ
14
У Джона есть чёрные и белые единичные кубики. Он хочет построить из них куб 3 × 3 × 3 так, чтобы ровно половина его поверхности была белая и половина чёрная. Какое наименьшее количество чёрных кубиков для этого ему понадобится?
A) 14 Б) 13 В) 12 Г) 11 Д) другой ответ
15
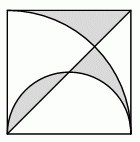
Внутри квадрата со стороной 6 см провели диагональ, построили полуокружность и четверть окружности так, как показано на рисунке. Чему равна площадь окрашенной части квадрата?
A) 9 см2
Б) 3π см2
В) (6π – 9) см2
Г) 10π/3 см2
Д) 12 см2
16
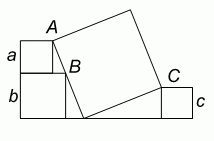
Четыре квадрата расположены так, как показано на рисунке. Стороны трёх меньших квадратов равны a, b и c. Какую длину имеет сторона большого квадрата?
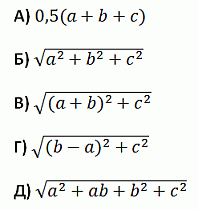
17
Числа p и q положительные, p < q. Какое из следующих выражений наибольшее?
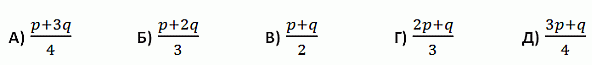
18
Сколько существует трехзначных чисел, содержащих хотя бы одну из цифр 1, 2 или 3?
A) 27 Б) 147 В) 441 Г) 557 Д) 606
19
Фёдор записал ненулевое 4-значное число N = pqrs. Он заметил, что если между q и r в этом числе поставить десятичную запятую, то получится число pq,rs, равное среднему арифметическому двузначных чисел pq и rs. Чему равна сумма цифр числа N?
A) 14 Б) 18 В) 21 Г) 25 Д) 27
20
Две свечи одинаковой длины начинают гореть одновременно со своей постоянной скоростью горения. Одна из свечей сгорает за 4 часа, другая – за 5 часов. Сколько часов обе свечи должны гореть до того момента, когда одна свеча станет в 3 раза короче другой?
A) 40/11 Б) 45/12 В) 63/20 Г) 3 Д) 47/14
21
У Андрея есть шесть карточек, на каждой стороне которых написано по одному числу. Пары чисел на карточках: (5, 12), (3, 11), (0, 16), (7, 8), (4, 14) и (9, 10). Карточки можно произвольным образом разложить на отмеченных местах в выражении
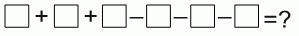
Какое наименьшее значение может иметь такое выражение?
A) –23 Б) –24 В) –25 Г) –26 Д) –27
22
Кенгуру решает уравнение
ax2 + bx + c = 0,
а Бобёр решает уравнение
bx2 + ax + c = 0,
где a, b, c – попарно различные ненулевые целые числа. Оказалось, что уравнения имеют общее решение. Какое из следующих утверждений заведомо верно?
A) общее решение равно 0
Б) уравнение ax2 + bx + c = 0 имеет ровно одно действительное решение
В) a > 0
Г) b < 0
Д) a + b + c = 0
23
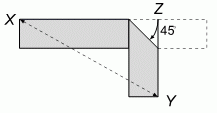
У меня есть полоска бумаги длиной 12 см и шириной 2 см. Я согнул её под углом 45° и сложил так, как показано на рисунке. Какое наименьшее значение может иметь расстояние между X и Y?
A) 6√2 см
Б) 7√2 см
В) 10 см
Г) 8 см
Д) 6 + √2 см
24
В кондитерской продаются ириски специальной марки в коробках по 6, 10 и 15 ирисок так, что невозможно, например, купить ровно 11 ирисок. Какое наибольшее количество ирисок невозможно купить в этой кондитерской?
A) 28 Б) 29 В) 31 Г) 34 Д) 37
25
Многочлен f(x) удовлетворяет уравнению
f(x + 1) = x2 – x + 2f(6)
при всех действительных x. Чему равна сумма коэффициентов многочлена f(x)?
A) -40 Б) -6 В) 12 Г) 40 Д) другой ответ
26
Числа x, y и z такие, что
2x = 3, 2y = 7 и 6z = 7.
Какое из следующих соотношений является верным?
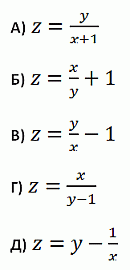
27
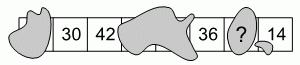
Полоска состоит из восьми клеток. Изначально в каждой клетке записано число 0. Каждым ходом можно выбрать четыре последовательные клетки и к каждому из чисел в выбранных клетках прибавить 1. На рисунке показан результат после нескольких ходов. К сожалению, некоторые клетки оказались залиты чернилами. Какое число записано в клетке со знаком вопроса?
A) 24 Б) 30 В) 36 Г) 48 Д) другой ответ
28
Функция f: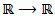 удовлетворяет равенству
удовлетворяет равенству
f(20 - x) = f(22 + x)
при всех действительных x. Известно, что f(x) имеет ровно два корня. Чему равна сумма этих корней?
A) –1 Б) 20 В) 21 Г) 22 Д) другой ответ
29
Двенадцать точек расположены на равном расстоянии по окружности. Сколько треугольников, имеющих угол 45°, можно образовать, выбрав три из этих точек?
A) 48 Б) 60 В) 72 Г) 84 Д) 96
30
Четырёхзначное число abcd удовлетворяет уравнению
abcd = aa + bb + cc + dd.
Какое значение имеет a?
A) 2 Б) 3 В) 4 Г) 5 Д) 6